Раздел 1_РЕД_2. I. основы теории множеств. Системы счисления комбинаторика

• Название: I. основы теории множеств. Системы счисления комбинаторика
• Анкор: Раздел 1_РЕД_2.doc
• Дата: 29.11.2017
• Размер: 9.96 Mb.
• Имя файла: Раздел 1_РЕД_2.doc
• Тип: Документы; #10536
• страница: 15 из 17

Пример 3. Рассмотрим расположение двух различных букв из множества A = {a, b, c} на двух различных местах m₁ и m₂.

Если все буквы различны и места различны, то:

C(А) = {(а, b); (а, c); (b, c); (b, a); (c, a); (c, b)}; N(С(А)) = 6.

Если места для расположения букв неразличимы (при этом, например, вариант (а, b) равен варианту (b, а)), то с учетом числа одинаковых мест s = 2 получим:

C(А(m₁ = m₂)) = {(а, b); (b, с); (а, с)}; N(С(А)) = 6 / 2!=3.

Если две последние буквы b и c одинаковы, то, подставляя вместо c букву b (так как c = b), с учетом числа одинаковых объектов p = 2 получим:

C(А(b = c)) = {(а, b); (b, b); (b, a)}; N(С(А)) = 6 / 2!=3.

Если все буквы а, b и c одинаковы (a = b = c), то с учетом числа одинаковых объектов p = 3 получим:

C(А(a = b = c)) = {(a, a)}; N(С(А)) = 6 / 3! =1.

Пример 4. На конференции присутствует 10 делегатов. Определить, сколькими способами можно сформировать из них состав комиссии в составе трех членов в двух случаях:

1) порядок членов комиссии (1-й, 2-й, 3-й) имеет значение;

2) все члены комиссии равноправны.

Решение. Вначале допустим, что число порядок членов комиссии имеет значение (случай 1). При этом число вариантов выбора первого члена комиссии N(a₁) = 10, для второго – N(a₂) = 9 (поскольку один делегат к этому времени уже занят), для третьего – N(a₃) = 8.

Общее число вариантов в случае 1 находим по правилу умножения:

N(С(А)) = N(a₁) × N(a₂) × N(a₃) = 10×9×8=720.

В случае 2) порядок расположения объектов не имеет значения и найденное выше число вариантов необходимо дополнительно разделить на 3!=6:

N(С(А)) = 720/6=120.

Ответ: 1) 720; 2) 120.

Применение рассмотренных выше правил 1) сложения, 2)включений-исключений, 3) умножения и 4) учета сходства-различия позволяют находить количественные оценки чисел вариантов во всех стандартных задачах комбинаторики на подсчет числа расположений объектов на выделенных местах, в которых множества объектов и мест для их размещения имеют простую структуру – учитывается только их число, сходство или различие.

Совместное применение данных правил позволяет также решать и усложненные комбинаторные задачи.

Пример 5. В комиссии по делам семьи 4 мужчины и 7 женщин. Необходимо избрать руководство комиссии – председателя и его заместителя. Определить, сколько существует возможных вариантов избрания руководства, если по положению в руководстве обязательно должны быть и мужчина и женщина.

Решение. Из положения следует, что для руководства возможны только два сочетания: 1) председатель – мужчина, заместитель – женщина; 2) председатель – женщина, заместитель – мужчина.

Рассмотрим сначала сочетание 1). На место председателя возможно избрание одного из 4 мужчин, на место его заместителя независимо может быть избрано 7 женщин. Порядок расположения имеет значение. Следовательно, по правилу умножения общее число вариантов для сочетания 1) равно 4×7=28.

Для сочетания 2) подсчет числа вариантов аналогичен: 7×4=28.

Общее число вариантов находим по правилу сложения, поскольку сочетания 1) и 2) являются взаимоисключающими.

Ответ: 28+28=56.

5.3. Размещения (размещения с повторениями)

Изучим основные типовые случаи расчета общего числа вариантов расположений объектов на выделенных местах.

Рассмотрим n мест a₁, a₂,…, a_n, для которых порядок расположения имеет значение и на которых могут независимо расположены представители из одного и того же множества, имеющего m объектов, при этом располагаемые объекты на разных местах могут иметь одинаковые значения (повторяться). Например, разряды десятичного числа, вносящие в него различный вклад, могут независимо принимать m = 10 значений от 0 до 9.

Данный способ расположения объектов называют размещением из n по m. Общее количество N(C(А)) вариантов всех рассматриваемых комбинаторных множеств C(А) обозначают U(n, m) либо . Поскольку значения величин могут неограниченное число раз повторяться при размещении на различных местах, то данный случай также можно назвать размещением с повторениями.

Поскольку для каждого места a₁, a₂, …, a_n число вариантов возможного расположения объектов не зависит от остальных и равно m, то, применяя (n-1) раз правило умножения, получим общую формулу для расчета :

.

Вывод расчетной формулы для общего числа вариантов 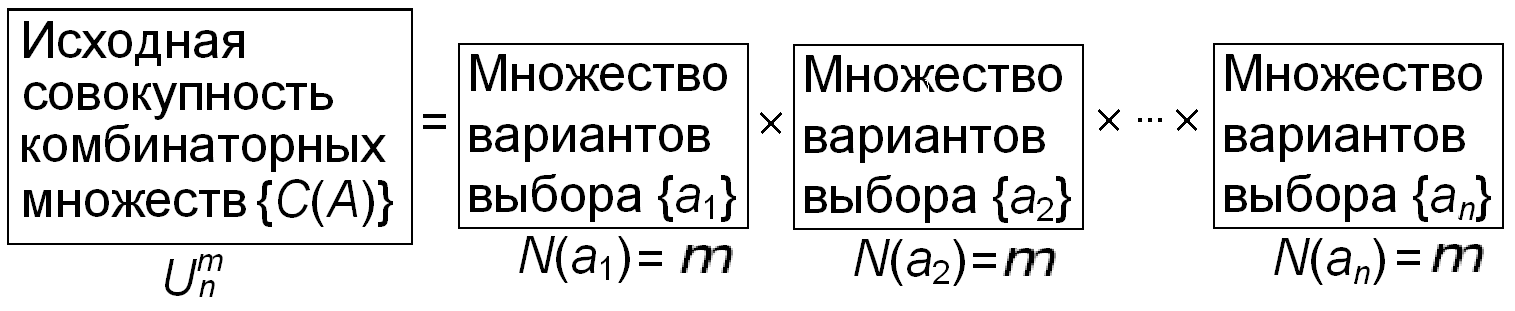размещений с повторениями m различных объектов на n местах с использованием правила умножения поясняется на схеме на рис. 5.7.



Рис. 5.7. Расчетная схема для подсчета общего числа вариантов размещений с повторениями m различных объектов на n местах

Многие практические задачи оценки количества объектов сводятся к подсчету размещений.

Пример 1. Найти количество N попарно различных трехзначных десятичных чисел для двух случаев:

1) когда в начале записей разрешены незначащие нули;

2) когда в записях незначащие нули недопустимы.

Решение.

1) Если нет ограничения на использование нулей, то в каждом разряде чисел может быть до 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Получаем задачу размещения со следующими параметрами: n = 3, k = 10. Следовательно:

.

2) Если использование незначащих нулей в начале записи чисел недопустимо, то в каждом из двух младших разрядов, как и в случае 1), может быть одна из 10 цифр, а в старшем разряде только одна из 9 цифр: (1, 2, 3, 4, 5, 6, 7, 8, 9). Поскольку цифры в разрядах независимы, то общее количество различных чисел в данном случае по правилу умножения составит:

N = 9×10² = 900.

Ответ: 1) 1000; 2) 900.

5.4. Перестановки и размещения без повторений различных объектов. Упорядоченность перестановок

Перестановкой длины n называют расположение n различных объектов на n различных местах. Общее количество N(C(А)) всех возможных попарно различных перестановок длины n обозначают как P(n), A(n, n) либо .

Размещением без повторений из n по k (n  k) называют расположение k взаимно различных объектов на n различных местах (не более одного объекта на место). Общее количество мест не меньше числа объектов. Полное количество N(C(А)) всех различных вариантов размещений без повторений из k по n обозначают как A (k, n) либо . Очевидно, что перестановки – частный случай размещений без повторений при равном количестве объектов и мест, т. е. k = n.

Подсчет общего числа вариантов расположения объектов в этом случае проще всего производить при помощи чисел вариантов N(a₁), N(a₂), …, N(a_k) расположения каждого из объектов 1, 2, ..., k.

Первый из размещаемых объектов можно разместить на любом из n имеющихся мест (число вариантов выбора N(a₁) = n). Для второго размещаемого объекта число вариантов выбора N(a₂) = n – 1, поскольку одно место уже занято. Для третьего по порядку размещаемого объекта
N(a₃) = n – 3, т. д., для k-го – N(a_k) = (n – k + 1).

По правилу умножения общее количество вариантов размещений без повторений из n по k равно произведению чисел вариантов N(a₁), N(a₂), ×××, N(a_k):

.

Вывод расчетной формулы для общего числа вариантов размещений без повторений k различных объектов на n местах с использованием правила умножения поясняется схемой на рис. 5.8.



Рис. 5.8. Расчетная схема для подсчета общего числа вариантов размещений без повторений k различных объектов на n местах

Общее число перестановок длины n:

.

Пример1. Определить, сколькими вариантами можно разместить четырех гостей за столом, если число стульев, занимающих различные положения (различающихся), равно: 1) 4; 2) 6?

Решение. В случае 1) имеет место расчет перестановок, так как количество объектов равно числу мест для размещения: k = n. Поэтому

.

В случае 2) число мест для размещения больше, чем число объектов (n > k), поэтому необходимо использовать формулу для расчета размещений без повторений из 6 по 4:

.

Ответ: 1) 24; 2) 360.

Замечание. Обычно при расчете размещений без повторений полагают, что мест n не меньше, чем объектов k (n  k). Однако на практике количество объектов k может быть больше, чем мест для размещения n (k > n). Данный случай можно рассматривать аналогично предыдущему, представив его как распределение n мест по k объектам. При этом количество возможных размещений равно k! / (k – n)!.

Таким образом, в задаче о распределении k неодинаковых объектов на n различных местах количество возможных размещений всегда можно представить в виде общей формулы:

,
где M = max(k, n); m = min(k, n).

Пример 2. Найти число вариантов размещения на 6 пронумерованных рабочих позициях станка различных инструментов, общее число которых равно 8.

Решение. Так как места и инструменты различны и k = 8 > n = 6, то M = max(k, n) = 8; m = min(k, n) = 6. Общее число вариантов размещения:

.

Ответ: 20160.

При подсчете вариантов вместо nнеодинаковых объектов всегда можно взять n различных натуральных чисел, например,
1, 2, ..., n.

Определение. Полной перестановкой _n (1, 2, ..., n) называют результат перестановки длины n чисел 1, 2, ..., n, куда каждое из них входит лишь раз. Общее количество перестановок {_n}равно = n!. Частичной перестановкой длины k ^k_n (1, 2, ..., n) будем называть результат размещениями без повторений k различных чисел из {1, 2, ..., n}. Общее количество перестановок {^k_n}равно = n!/(n-k)!.

Пару элементов в перестановке (а_i, а_j) будем считать упорядоченной, если а_i < а_jпри i < j. Каждую полную перестановку чисел (1, 2,..., n) =(₁, ₂, ...,_n) можно взаимно однозначно охарактеризовать вектором инверсий d = (d₁, d₂, ..., d_n), определяющим меру неупорядоченности перестановки . Это соответствие устанавливают следующим образом: каждый элемент d_i равен числу элементов, стоящих слева от _i и превышающих его (т. е. нарушающих порядок). У первого элемента d₁= 0. Полностью упорядоченной перестановке чисел (1, 2, ..., n) соответствует d_min = (0, 0, ..., 0), а максимально неупорядоченной перестановке (n, n–1, ..., 1) — вектор инверсий d_max =(0, 1,…, n–2, n–1). Каждый вектор инверсий можно рассматривать как обращенную слева – направо запись некоторого числа N(d) в факториальной системе счисления. Вектору N (d_min) соответствует 0, вектору N(_max) — число (n!–1). Следовательно, множество всех полных перестановок (1, 2, ..., n)можно взаимно однозначно отобразить на множество всех целых чисел от 0до (n! –1).

Определение. Весом вектора инверсий d = (d₁, d₂, ..., d_n) называют сумму его компонент:

 _и (d ) = d₁ + d₂ + ... + d_n .

Вес вектора инверсийперестановки  = (₁, ₂, ..., _n) равен количеству перемен мест рядом стоящих элементов, необходимому для полного упорядочения перестановки, соответствующей вектору d.

Пример 3.

1) d(4,5,1,3,6,2) = (0,0,2,2,0,4), N = 22! + 23! + 45! = 22 + 26 + 4120 = 496₁₀, _и (d) =8,

2) d(3,1,6,5,2,4) = (0,1,0,1,3,2) , N = 11! + 13! + 34! + 25! = 11 + 16 + 324 + 2120 = 319₁₀ ,_и (d) = 7.

Определение. Лексикографическим будем называть порядок перестановок  (1, 2, ..., n) = (₁, ₂, ...,_n), когда соответствующие им числа в факториальной системе счисления расположены по возрастанию от 0 до (n! –1).