Раздел 1_РЕД_2. I. основы теории множеств. Системы счисления комбинаторика

• Название: I. основы теории множеств. Системы счисления комбинаторика
• Анкор: Раздел 1_РЕД_2.doc
• Дата: 29.11.2017
• Размер: 9.96 Mb.
• Имя файла: Раздел 1_РЕД_2.doc
• Тип: Документы; #10536
• страница: 13 из 17

4.4.2 Вычитание

Если числа представлены в разных системах счисления, их предварительно необходимо привести в одну систему счисления. Как и при сложении, записываем одно число под другим таким образом, чтобы разряды с одинаковыми номерами располагались друг под другом. При вычитании большего числа из меньшего результату присваиваем знак «–» и меняем числа местами. Вычитание производим поразрядно, передвигаясь от нулевого разряда к старшим. Если из меньшего числа в разряде вычитается большее, занимаем из следующего старшего разряда одну единицу, равную p единицам текущего разряда.

Пример 4. Вычесть число 8BA39₁₆ из C5D₁₆.

Решение. Так как большее число вычитается из меньшего, присваиваем результату знак «–» и меняем числа местами. Вверху указываем единицы, занимаемые из старших разрядов.

111

8BA39

– C5D

8ADDC

Действия в разрядах:

разряд 0 (занимаем единицу в разряде 1): 9₁₆+10₁₆ –D₁₆ = 
=9₁₀ + 16₁₀–13₁₆=12₁₀ = C₁₆;

разряд 1 (занимаем единицу в разряде 2): 2₁₆ + 10₁₆–5₁₆ = 
2₁₀ + 16₁₀–5₁₀ =13₁₀ = D₁₆;

разряд 2 (занимаем единицу в разряде 3): 9₁₆+10₁₆–C₁₆ = 
=9₁₀+16₁₀–12₁₀=13₁₀=D₁₆;

разряд 3: A₁₆;

разряд 4: 8₁₆.

Ответ: C5D₁₆–8BA39₁₆ = –8ADDC₁₆.

4.4.3. Прямой и дополнительный коды целых чисел. Их представление в памяти компьютера, сложение и вычитание

В электронной памяти числа всех типов (логические, целые (беззнаковые и со знаком), вещественные) всегда занимают целое число байтов. Минимальный объем памяти, занимаемый одним числом, равен одному байту (8 битам).

В формате “беззнаковое целое число” запись положительного целого числа представляет собой его двоичный код, размещенный в байтах, отведенных для него. При этом в одном байте можно разместить двоичные коды всех положительных чисел от 0 (00000000) до 2⁸–1 = [phone]). Например, 00100010₂ = +34₁₀, 11001100₂ = +204₁₀.

В формате “целое число со знаком” знак числа всегда задается в старшем разряде старшего байта: он равен 0 у положительных чисел и 1 у отрицательных. Остальные разряды записи заполняются в зависимости от типа кода. Основными являются прямой код и дополнительный.

Прямой код – это такое представление целого числа со знаком, в котором старший разряд старшего байта отводится под знак числа, а все оставшиеся разряды – под двоичную запись его абсолютной величины (модуля). Например, для однобайтового представления знак помещается в старшем разряде 7, а модуль – в разрядах с 0 по 6: 00001010₂ = +1010, 10001010₂ = –1010. При этом диапазон значений охватывает от
(–127₁₀) = 11111111₂ до (+127₁₀)=01111111₂.

Для общности прямым кодом беззнакового целого числа можно считать его двоичную запись. Сложение байтовых беззнаковых целых чисел производится по модулю числа 2⁸ =256. При этом единичные значения, возникающие в разряде 8, выходящем за состав байта, отбрасываются. Например:

10010110₂ + 01110111₂ = 1 00001101₂ = 00001101₂ (mod 2⁸).

Это свойство используется у беззнаковых целых чисел для замены операции вычитания операцией сложения чисел по следующему правилу:

a – b (mod 2⁸) = a + (–b)(mod 2⁸) = a + (2⁸ – b)(mod 2⁸).

Выражение (2⁸–b) называют дополнительным кодом отрицательного числа (–b), соответствующего байтовому беззнаковому числу b. Его можно получить:

1) инвертированием двоичной записи всех разрядов числа b (при котором получается число вида 2⁸ – 1 – b) и последующим

2) прибавлением к нему 1, после чего получаем искомую величину
(2⁸ – b).

Дополнительный код положительного числа совпадает с прямым.

Пример 5. Выполнить вычитание (10–37) байтовых беззнаковых чисел с использованием дополнительного кода. Найти результат в дополнительном коде, а также его модуль в прямом коде.

Решение. Прямой двоичный код беззнакового числа 10 равен 00001010₂. Прямой код числа 37 равен 00100101₂. Найдем его дополнительный код:

Инверсия всех разрядов: 11011010₂. Добавление единицы: 11011011₂.

Результат сложения: 00001010₂ [phone] =11100101₂.

Так как большее число вычиталось из меньшего, ответ отрицательный. Для определения абсолютной величины ответа переведем его в прямой код.

Вычитание: 11100100₂. Инвертирование: 00011011₂.

Полученное значение модуля результата равно 27₁₀.

Ответ: а) 11100101₂, б) 00011011₂.

Пример 6. Выполнить вычитание (144–17) байтовых беззнаковых чисел с использованием дополнительного кода. Найти результат в дополнительном и прямом кодах.

Решение. Прямой двоичный код беззнакового числа 144 равен 10010000₂. Прямой код числа 17 равен 00010001₂. Найдем его дополнительный код:

Инверсия всех разрядов: 11101110₂. Добавление единицы: 11101111₂.

Результат сложения: 10010000₂ + 11101111₂ = 01111111₂.

Так как из большего числа вычиталось меньшее, ответ положительный. При этом результат получается в прямом коде, который совпадает с дополнительным. Полученное число равно 127₁₀.

Ответ: а) 01111111₂, б) 01111111₂.

Сложение байтовых целых чисел со знаком производится по модулю числа 2⁷ = 128 (без учета старшего знакового разряда). При этом единичные значения, возникающие в знаковом старшем разряде 7, отбрасываются. Выражение (2⁷ – b) является дополнительным кодом отрицательного числа со знаком, равного (–b). Практически дополнительный код отрицательного числа со знаком (–b) получается следующим образом:

1) занесением в старший знаковый разряд 7 значения 1, означающего отрицательное число;

2) инвертированием двоичной записи всех разрядов числа b помимо знакового старшего (при котором в данных разрядах будет получена запись числа 2⁷ – 1 – b) и 3) прибавлением 1 к полученному в младших разрядах числу, после чего получаем в них искомую величину (2⁷ – b).

При сложении чисел с одинаковым знаком этот же знак присваивается и результату. При сложении чисел с разными знаками в качестве знака результата принимается знак большего по модулю складываемого числа. Например, вычитание целых со знаком чисел (96₁₀ – 22₁₀) можно представить в виде сложения прямого кода первого числа с дополнительным кодом числа (–22₁₀), причем знак результата совпадает со знаком большего по модулю первого числа. Учитывая, что дополнительный код числа
(–22₁₀) = 1101010₂, получим:

96₁₀ – 22₁₀ = 96₁₀ + (–22)₁₀ = 01100000₂ + 11101010₂ = 01001010₂=74₁₀.

Двоичное 8-ми разрядное число со знаком в дополнительном коде может представлять любое целое в диапазоне от −128 до +127. Если результат вычитания является отрицательным числом, то он получается в дополнительном коде и для оценки модуля результата его переводят в прямой код.

Примеры байтового представления целых чисел со знаком:

Десятичное представление	Код байтового двоичного представления целых чисел со знаком
	прямой	дополнительный
127	01111111	01111111
1	00000001	00000001
0	00000000	00000000
−0	10000000	00000000
−1	10000001	11111111
−3	10000011	11111101
−7	10000111	11111001
−8	10001000	11111000
−10	10001010	11110110
−127	11111111	10000001
−128	---	10000000

Пример 7. Представить байтовое отрицательное число со знаком (−21) в а) прямом и б) дополнительном кодах.

Решение. Прямой код отрицательного числа со знаком (−21) равен его двоичной записи с единицей в старшем разряде: 10010101₂. Строим дополнительный код:

Инверсия его разрядов 0–6: 11101010₂.

Добавление единицы: 11101011₂.

Ответ: а) 10010101₂, б) 11101011₂.

Пример 8. Найти в дополнительном и прямом кодах результат вычитания (5 – 21) байтовых целых чисел со знаком с использованием дополнительного кода.

Решение. Из примера 7 берем дополнительный код отрицательного числа со знаком (−21): 11101011₂. Выполняя его сложение с прямым кодом положительного числа 5, получим дополнительный код итогового числа.

00000101

[phone]

11110000

Полученный дополнительный код переводим в прямой: Вычитание единицы: 11101111₂. Инверсия его разрядов 0–6: 10010000₂.

Получен прямой код отрицательного числа (–16).

Ответ: а) 11110000₂, б) 10010000₂.

4.5. Двоичные (булевы) векторы

Двоичным (булевым) n-мерным вектором называют набор из n чисел (b₁, b₂, ..., b_n), каждое из которых может принимать только значения в двоичной системе счисления – 0 или 1.

Двоичный вектор является обратным (инвертированным) к , если он образован из заменой всех нулей единицами, а единиц – нулями.

Например, если  = (0, 1, 1, 1, 0, 1), то  = (1, 0, 0, 0, 1, 0).

Если в записи двоичного вектора длины n устранить запятые, его можно рассматривать как двоичную запись некоторого целого числа. Наименьшим таким числом является 0. Ему соответствует вектор  = (0, ..., 0). Наибольшим является число 2ⁿ – 1, которому соответствует вектор  = (1, ..., 1). Следовательно, при помощи полного набора двоичных векторов длины n можно записать все 2ⁿ целых чисел из отрезка
[0,2ⁿ–1]. Такие числа называют порядковыми номерами векторов. Их используют как в двоичном виде, так и в десятичной системе счисления.

Пример 1. Найти порядковый номер булева вектора  = (1, 0, 0, 1, 0, 1) в десятичной системе счисления.

Решение. Устраняя запятые в векторе, получим двоичную запись 100101₂. Переводя ее по правилу 2.1.1 в десятичную систему счисления, получим:

100101₂ = 12⁵ + 12² + 12⁰ = 32₁₀ + 4₁₀ + 1₁₀ = 35₁₀.

Ответ: десятичный порядковый номер заданного булева вектора равен 35₁₀.

В качестве меры близости булевых векторов используют расстояние Хэмминга.

Определение. Расстоянием Хемминга  между булевыми векторами  ⁿи ⁿ называют величину ( ⁿ,  ⁿ), которая равна числу координат, по которым различаются векторы  ⁿи ⁿ.

Пример 8.  (100011, 110011)=1, (0101, 1010)=4.

Определение. Булевы векторы ⁿи ⁿ , различающиеся ровно по одной координате (  (ⁿ,ⁿ) = 1), называют соседними.

Рассмотрим наиболее употребительные геометрические интерпретации булевых n – мерных векторов.

1. Представление в виде двоичных чисел. Если в записи вектора bⁿ устранить запятые, ее можно рассматривать как двоичную запись некоторого целого числа. Наименьшим таким числом является 0. Ему соответствует вектор bⁿ =(0, ..., 0). Наибольшим является число 2ⁿ – 1, которому соответствуетbⁿ = (1, ..., 1). Следовательно, при помощи векторов bⁿ можно записать все 2ⁿ целых чисел из интервала [0, 2ⁿ– 1]. Такие числа будем называть порядковыми номерами векторов.

Лексикографическим называют такой порядок векторовbⁿ, когда соответствующие им двоичные числа расположены по возрастанию от 0 до 2ⁿ – 1.

В качестве примера рассмотрим полное множество 3-мерных двоичных векторов, расположенных в лексикографическом порядке:

0 (0, 0, 0), 4 (1, 0, 0),

1 (0, 0, 1), 5 (1, 0, 1),

2 (0, 1, 0), 6 (1, 1, 0),

3 (0, 1, 1), 7 (1, 1, 1).

2. Бинарное дерево Тⁿ. Сопоставим множеству всех 2ⁿвекторовbⁿ следующую древовидную структуру, начинающуюся
в корневой вершине О (вершине нулевого уровня). Из нее выходят вниз два отрезка (ребра), соответствующие значениям b₁=0(влево) и b₁=1(вправо) и оканчивающиеся вершинами первого уровня. Из них выходят вниз по два ребра, соответствующие b₂=0(влево) и b₂=1(вправо) и оканчивающиеся новыми вершинами — второго уровня и т. д. Процесс завершается построением всех вершин n-го уровня. Данная структура называется
бинарным деревом и обозначается Тⁿ. На рис. 4.1 показано
дерево Т³для 3-мерного булевого вектораb³=(х, у, z).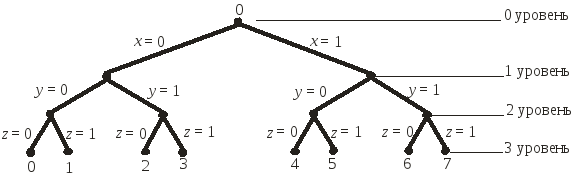



Рис. 4.1. Бинарное дерево Т³

Пронумеруем слева направо все вершины n-го уровня от 0до
2ⁿ – 1. Каждому вектору bⁿ можно однозначно поставить
в соответствие путь из корневой вершины О в вершину n–го уровня с порядковым номером вектора bⁿ. Например, вектору (0,1,0) в рассмотренном примере соответствует путь из корневой вершины в вершину 2 (010₂ = 2₁₀) по ребрам х = 0, у = 1, z = 0. Таким образом, бинарное дерево полностью описывает все 2ⁿвекторовbⁿ.

3. Единичный n-мерный куб Вⁿ. Единичным n-мерным кубом называют полный набор вершин, соответствующих векторамbⁿ, в котором каждые две соседних вершины (которым соответствуют векторы, различающиеся ровно по одной координате) соединены отрезком (ребром). Обозначается единичный n-мерный куб как Вⁿ. На рис. 4.2 показаны кубы В¹, В², а также плоские проекции кубов В³, В⁴.

Определение. Дана вершинаⁿв Вⁿ. Множество вершин Вⁿ{ⁿ}, для которых (ⁿ,ⁿ)= r, называют сферой радиуса r. Множество {ⁿ} вершин Вⁿ, для которых (ⁿ,ⁿ) r, называют шаром радиуса r.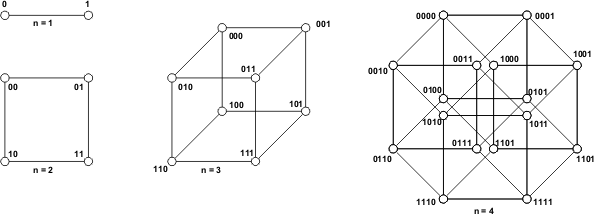



Рис. 4.2. Единичные n-мерные кубы В¹, В² и плоские проекции кубов В³, В⁴

Вопросы для проверки знаний.

1. Есть ли принципиальное различие правил выполнения сложения и вычитания в десятичной системе счисления и других системах с постоянными основаниями?

2. Какой формат компьютерного представления чисел называют беззнаковым целым числом?

3. Какой формат компьютерного представления чисел называют целым числом со знаком?

4. Какой способ компьютерного представления целых чисел называют прямым кодом?

5. Какой способ компьютерного представления целых чисел называют дополнительным кодом?

6. Для каких целых чисел прямой код совпадает с дополнительным кодом?

7. Может ли целое число занимать в электронной памяти а) 4 бита, б) 6 бит, в) 8 бит, г) 10 бит?

8. По каким правилам осуществляется перевод беззнаковых байтовых целых чисел из прямого кода в дополнительный и обратно?

9. По каким правилам осуществляется перевод байтовых целых чисел со знаком из прямого кода в дополнительный и обратно?

10. В каких случаях вычитание байтовых беззнаковых целых чисел дает результат в прямом коде, а в каких – в дополнительном?

11. Что называют двоичным (булевым) n-мерным вектором?

12. Какую операцию называют инвертированием булевого вектора?

13. Какие числа называют порядковыми номерами булевых векторов?

14. Что называют лексикографическим порядком двоичных векторов?

Практические задания.

1. Сложить в системе с основанием 16 числа 23301₄ и 1435₈.

2.Сложить в восьмеричной системе числа 101101101₂ и 9СВ₁₆.

3. Выполнить вычитание (192–103) байтовых беззнаковых чисел с использованием дополнительного кода.

4. Найти порядковый номер двоичного вектора (0, 0, 1, 0, 1, 1, 0) в десятичной системе счисления.

5. Упорядочить по возрастанию порядковых номеров булевы векторы длины 5: (0, 0, 1, 0, 1), (0, 1, 1, 0, 1), (1, 0, 1, 0, 0).

4.6. Смешанные позиционные системы счисления. Факториальная система

Важным обобщением позиционных систем с постоянным основанием являются смешанные системы, где основания меняются от разряда к разряду. Обозначим основания разрядов с номерами 0, 1, ..., k через р₀, р₁, ..., р_k. Тогда запись вида А_p=_k...₂₁₀означает представление в смешанной системе счисления величины _kр_(k-1) ... p₁р₀+ ...+₂p₁р₀+₁р₀ + ₀. Каждый коэффициент _i удовлетворяет неравенcтву: 0 _i p_i . Наиболее известным примером смешанной системы счисления является общепринятая система измерения времени: «секунды – минуты – часы – сутки – недели – годы», основаниями в которой являются числа р₀= 60, р₁= 60, р₂= 24, р₃ = 7, р₄=52.

4.6.1. Перевод целых чисел из десятичной системы в смешанную с основаниями р₀, р₁, ... ,р_k

Проще всего осуществить такой перевод последовательным делением числа и его частных на основания р₀, р₁, ..., р_k . Остатки от деления на каждом шаге и самое последнее частное в итоге образуют искомую запись числа в смешанной системе.

Пример 1. Выразим временной период А = 1 526 840 секунд в общепринятой системе измерения времени «сек — мин — ч — сут. — нед. —
— годы», где р₀ = 60, р₁ = 60, р₂ = 24, р₃= 7, р₄=52.

Решение. 1526840 60

1526820 25447 60

20 25440 424 24

7 408 177

16 142

3.

Рассматривая в обратном порядке остатки от деления на каждом шаге и самое последнее частное, получим искомую запись числа:

А =₄₃₂₁₀=2/3/16/07/20 = 2недели 3 дня 16 часов 7 минут 20 секунд.

Обратный перевод из смешанной системы в десятичную осуществляют посредством умножения каждого символа _k на сомножитель, представляющий собой произведение р_kр_(k–1)∙∙∙p₁р₀,
с последующим суммированием полученных произведений.

С точки зрения практического применения в комбинаторных задачах из смешанных систем счисления для представления целых чисел наиболее важна факториальная, где стоимость каждого разряда с номером i равна i!. При этом основание разряда равно p_i = i + 1.Запись _k∙∙∙₂₁₀. в факториальной системе обозначает число А_ф=_kk! +...+₂ 2!+ ₁1!+₀. Поскольку в математике принято соглашение 0! = 1, то в факториальной системе всегда задается ₀=0. Правила перевода из десятичной системы счисления в факториальную и обратно аналогичны правилам для всех смешанных систем.

Пример 2. Перевести в факториальную систему счисления
число А = 627₁₀.

Решение. 

627 1

627 6272

0 6263133

1 3121044

1 104265

0 255

1

Ответ: Искомое представление числа в факториальной системе имеет вид: А _ф= 510110.

Обратный перевод выполняется следующим образом:

А = 55! + 14! + 0  3! + 12! + 1 1! =5120 + 124 + 12 + 11 = = 600 + 24 + 2 + 1 = 627₁₀.

Факториальная запись чисел удобна для подсчета вариантов множеств, состоящих из взаимно отличных друг от друга объектов.

Задачи

1. Перевести в двоичную систему числа:

а) 1052₁₀, б) 0,965₁₀, в) 31,53₁₀, г) 159,66₁₀.

2. Перевести в десятичную систему числа:

а) 1100110₂, б) 0,0010₂, в) 10101,011₂, г) 110,0101₂.

3. Доказать, что в n – мерном кубе Вⁿ :

а) количество вершин в сфере радиусом 1 равно n, а количество вершин в шаре радиусом 1 равно n +1;

б) количество вершин в сфере радиусом 2 равно n (n – 1)/2,
а количество вершин в шаре радиусом 2 равно n(n+1)/2+1.

4. Доказать (например, с использованием метода математической индукции), что общее количество вершин в бинарном дереве Тⁿравно 2ⁿ⁺¹–1.

5. Доказать методом математической индукции, что в n-мерном кубе Вⁿ число ребер равно n∙2^n–1.

6. Доказать, что на множестве всех n-мерных булевых векторов расстояние Хэмминга удовлетворяет неравенству треугольника:

 (ⁿ,ⁿ) +  (ⁿ, ⁿ)   (ⁿ,ⁿ),

гдеⁿ,ⁿ,ⁿ — любые векторы из bⁿ .

7. Пусть Вⁿ— множество всех n – мерных двоичных векторов
bⁿ, которые появляются случайно c одинаковой вероятностью. Доказать, что средневероятный вес _св(b ⁿ) булевых векторовbⁿ равен n/2.

8. Перевести в двоичную систему и систему с основанием 4 числа B23DA₁₆, АD7С₁₆.

9. Перевести в десятичную систему числа F9B83₁₆, CАF5₁₆.

10.Перевести в шестнадцатеричную систему числа 110110₂ , 1101101₂ , 1011011010101₂ .

11.Перевести, используя сокращенные правила перевода, из восьмеричной системы в двоичную числа 5716₈, 173₈ , 265₈ .

12. Перевести следующие дроби в десятичную систему:

а) 0,16₈, б) 0,21₃, в) 0,43₆, г) 0,5₇.

13. Выполнить следующие арифметические действия:

а) 12021101₃ – 210012231₃ , 7435813₉ – 525048₉ ;

б) 10111101₂  1101₂ , A4D3₁₆  C5A₁₆ ;

в) 5362 ₇ : 65₇ , 67516 ₈ : 47₈ .

14. Перевести в факториальную систему числа:

а) 172₁₀, б) 934₁₀, в) 2157₈, г) 1535₆.

15. Перевести в десятичную систему из факториальной числа:
а) 423010, б) 231200, в) 142110, г) 502110.