Раздел 1_РЕД_2. I. основы теории множеств. Системы счисления комбинаторика

• Название: I. основы теории множеств. Системы счисления комбинаторика
• Анкор: Раздел 1_РЕД_2.doc
• Дата: 29.11.2017
• Размер: 9.96 Mb.
• Имя файла: Раздел 1_РЕД_2.doc
• Тип: Документы; #10536
• страница: 14 из 17

Глава 5. КОМБИНАТОРИКА

Комбинаторикой называют математическую дисциплину, изучающую свойства множеств, которые можно построить из заданного базового набора дискретных объектов. Отдельные задачи количественного анализа таких множеств известны еще с древности. В современной комбинаторике рассматривается большое число общих и конкретных задач из области как естественных, так и гуманитарных наук. Необходимость в подобного рода подсчетах обычно возникает при определении вероятности, оценках, подсчетах, задачах планирования и т. д.

5.1. Основная задача комбинаторики. Характеристики комбинаторных задач

Обозначим через A начальное базовое множество дискретных объектов. В простейшем случае – это обычный набор объектов, заданный перечислением.

Способ порождения из заданного базового набора A новых множеств (комбинаторных множеств) называют комбинаторным правилом. Обозначим его через С. Полную совокупность комбинаторных множеств, которые могут быть образованы из A при помощи правила C, обозначим через C(А), а общее число комбинаторных множеств в ней обозначим через N(C(А)).

Поскольку комбинаторика, в первую очередь, рассматривает количественные свойства совокупностей комбинаторных множеств, то основную задачу комбинаторики (комбинаторного анализа) можно сформулировать следующим образом: по заданному базовому множеству объектов A и комбинаторному правилу C определить общее число элементов N(C(A)) в порождаемом комбинаторном множестве C(А).

Пример 1.

1) базовое множество A = {натуральные числа 3, 4, 5, 6, 7},

2) комбинаторное правило C = “подбор пары взаимно простых чисел из A”,

3) полная совокупность производных множеств (комбинаторное множество) C(А) = {(3, 4); (3, 5); (3, 7); (4, 5); (4, 7); (5, 6); (5, 7); (6, 7)},

4) число элементов в порождаемом комбинаторном множестве N(C(А)) = 8.

Для решения основной задачи комбинаторики о расчете N(C(А)) по заданным A и C в общем случае используются соотношения из теории множеств, алгебраические методы (в основном – составление рекуррентных соотношений), методы производящих функций и др. Ниже будут рассмотрены основные расчетные правила.

Чаще всего на практике требуется определить общее число вариантов расположения элементов заданного базового множества на выделенных местах либо выборки заданного множества объектов из некоторой более широкой совокупности. При формулировании комбинаторного правила C указываются простейшие условия на сходство или различие объектов в A, а также количественные ограничения на выборку.

Пример 2.

1) базовое множество A = {буквы, входящие в слово “абзац”},

2) комбинаторное правило C = “формирование пар различающихся букв из заданного слова”,

3) комбинаторное множество C(А) = {(а, б); (а, з); (а, ц); (б, з); (б, ц); (з, ц)},

4) число элементов в порождаемом комбинаторном множестве N(C(А)) = 6.

С точки зрения подсчета числа вариантов N(C(А)) всех комбинаторных объектов для заданного множества объектов A и выделенных мест для их расположения при заданном комбинаторном правиле C существенными являются следующие характеристики задачи.

1. Количественные характеристики: число объектов k и число мест n для их размещения. Параметр k называют объемом выборки.

2. Качественные характеристики: сходство либо различие, как между размещаемыми объектами, так и между выделенными для них местами.

Рассмотрим свойство 2) сходства-различия. Как правило, в каждой конкретной комбинаторной задаче вводятся явно или понятны из постановки существенные признаки объектов и мест, по значениям которых можно однозначно определить для них одинаковость, сходство (при совпадении всех существенных признаков) либо различие (все или часть признаков отличны).

Пример 3. Если при размещении студентов первого курса в актовом зале существенным признаком для студентов принять только курс обучения, то по нему все студенты (как объекты размещения) одинаковы. Если же существенным признаком являются паспортные данные, то по нему все студенты различны. Аналогично, если для каждого кресла в актовом зале учитывается его ряд и место в нем, то все места для размещения в задаче подсчета следует считать различными. Если же положение кресел в зале не важно, то в задаче все места для размещения будут одинаковы.

Пример 4. Рассмотрим процесс образование новых слов из заданного путем перестановки в нем букв. В данной задаче у слова «абзац» две буквы «а» на первой и четвертой позиции неразличимы, поскольку при их перестановке слово остается прежним, т. е. не возникает новый комбинаторный объект. Перестановка любых других пар букв порождает новое слово, поэтому в данной задаче они являются различными.

Поскольку свойства дискретных наборов и способы формирования множеств из них различны, то при определении общего количества конкретных вариантов множеств необходимо уметь правильно сводить реальные практические задачи к стандартным расчетным схемам и применять соответствующие методы подсчета.

5.2. Основные правила подсчета чисел комбинаторных множеств

Рассмотрим основные формулы комбинаторики, позволяющие найти правильное решение как ее главной проблемы, так и других вспомогательных задач.

5.2.1. Правило сложения

Допустим, всю совокупность подсчитываемых комбинаторных множеств C(А) можно разделить на n частей С₁(А), С₂(А), ..., С_n(А), содержащих, соответственно, N(С₁(А)), N(С₂(А)), …, N(С_n(А)) множеств, таким образом, что данные части не пересекаются друг с другом и в сумме дают все множество C(А).

Тогда общее число N(C(А)) всех подсчитываемых множеств равно сумме данных значений N(С₁(А)), N(С₂(А)),…, N(С_n(А)):

N(С(А)) = N(С₁(А)) + N(С₂(А)) + … + N(С_n(А)).

Данную формулу называют правилом сложения.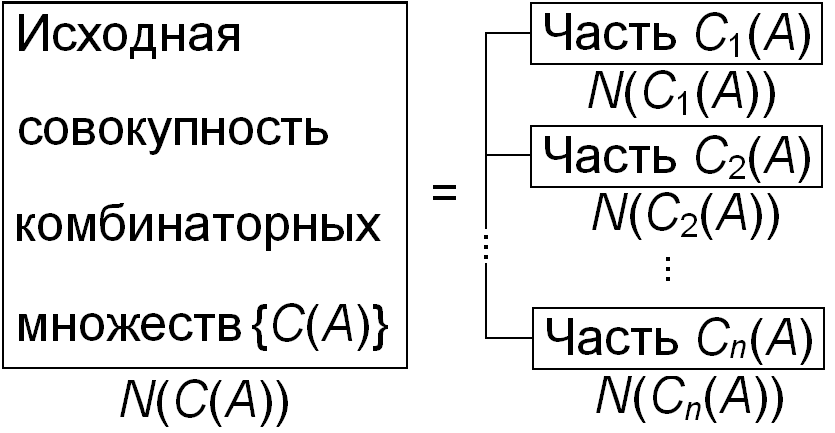


Рис. 5.1. Расчетная схема правила сложения

5.2.2. Формула включений-исключений

Из правила сложения с применением других теоретико-множественных операций может быть выведена формула включений-исключений (или принцип (правило) включений-исключений). Это правило позволяет рассчитать количество элементов в объединении конечных множеств, которые в общем случае могут пересекаться друг с другом. При двух множествах A и B (рис. 5.2) правило имеет вид:

N(AB) = N(A) + N(B) – N(AB),
где N(A), N(B), N(AB), N(AB) – числа элементов в исходных множествах А и В, их объединении AB и пересечении AB.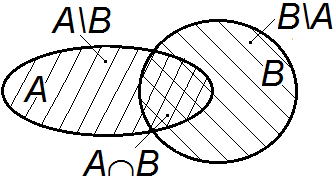



Рис. 5.2. Объединение двух множеств A и B

Поскольку вывод данной формулы требует применения дополнительных теоретико-множественных операций разбиения множества на разность и пересечение, то правило включений-исключений нельзя вывести из правила сложения средствами самой теории (комбинаторики). Для сведения правила включений-исключений к параллельной схеме расчета в формуле необходимо использовать разности множеств (рис. 5.2):

N(AB) = N(A\B) + N(B\A) + N(AB),
где A\B – результат вычитания множества B из множества A, B\A – результат вычитания множества A из множества B.

В полученной формуле комбинаторным правилом является объединение, а операции вычитания и пересечения играют вспомогательную роль. При этом расчетная схема принимает стандартный для параллельных вычислений вид (рис. 5.3):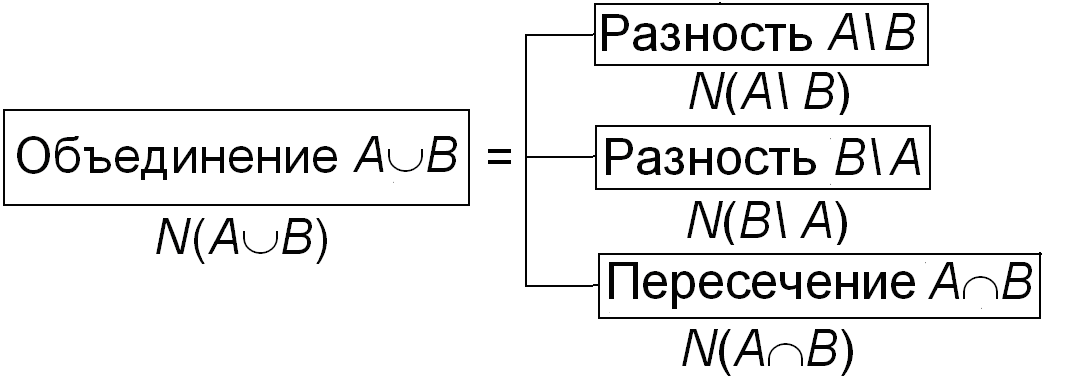



Рис.5.3. Расчетная схема правила включений-исключений для двух множеств

В случае количества множеств s > 2 процесс нахождения количества элементов объединения A₁  A₂  …  A_s заключается в начальном суммировании чисел всех элементов, затем исключении лишнего, затем включении ошибочно исключенного и так далее, то есть в попеременном включении и исключении. Данный процесс дал название формулы.

Пример 1. На выставке представлено 23 картины, в которых использованы только красный и синий цвета. Из них 8 выполнены только в красном цвете, на 11 одновременно использован и красный и синий цвет. Сколько выставлено картин, в которых использован синий цвет?

Решение. Обозначим множество картин, в которых использован красный цвет (только красный и вместе с синим), через A, а множество картин, в которых есть синий цвет, через В. В условии задано общее число картин: N(A  B) = 23, число картин в разности N(A\B) = 8 и число картин в пересечении N(A  B) = 11. Подставляя данные значения в формулу для N(A  B), выраженную через разности множеств, получим вначале число картин, в которых использован только синий цвет:

N(B\A) = N(A  B) – N(A\B) – N(A  B) = 23 – 8 – 11 = 4.

Искомое общее число картин, в которых использован синий цвет, равно:

N(B) = N(B\A) + N(A  B) = 4 + 11 = 15.

Ответ: 15.

5.2.3. Правило умножения
Пусть правило порождения комбинаторных множеств вида C(А) = {a₁, a₂,…, a_k} представимо через последовательный выбор его элементов a₁, a₂, …, a_k из исходного множества A, причем числа вариантов выбора N(a₁), N(a₂) ,…, N(a_k) не зависят от того, какой из элементов выбран на каждом шаге. Тогда общее количество N(C(А)) вариантов всех подсчитываемых комбинаторных множеств C(А) равно произведению:

N(А) = N(a₁) ∙ N(a₂)  ∙ ... ∙ N(a_k).

Замечание. При количественной независимости чисел вариантов выбора N(a₁), …, N(a_k) качественный состав a₁, …, a_k может быть зависимым, например, при выборке из исходного множества, где все элементы различны.

Правило умножения реализует последовательный принцип вычислений, при котором общее число вариантов получается путем умножения частных. Его расчетная схема дана на рис. 5.4.



Рис. 5.4. Расчетная схема правила умножения
Пример 2. Для выбора первой и второй компонент вектора (а₁, а₂) используются базовые числовые множества А₁ = {1, 2} и А₂ = {3, 4, 5}.

1. При независимом выборе величин а₁ и а₂ общее количество вариантов векторов по правилу умножения равно N(C(А)) = N(a₁) × N(a₂) = 23=6;

2. При наличии дополнительного условия а₁ + а₂ = 6 набор комбинаторных множеств C(А) = {(1, 5); (2, 4)}. Общее количество вариантов векторов N(C(А)) = 2. Оно не подчиняется правилу умножения.

5.2.4. Правило учета сходства и различия

Допустим, рассматриваются все варианты расположения на заданных местах объектов некоторого множества A, содержащего подмножество из p объектов {a} = {а₁, а₂,…, а_p} ({a}  А). Обозначим условно через C(A(а₁  а₂ …  a_p)) комбинаторное множество, образованное из A при условии различия всех объектов в подмножестве {a}, а через C(A(а₁ = а₂ = … = а_p)) – аналогичное множество, полученное из A при условии неразличимости, одинаковости объектов в {a}.

Для общих чисел вариантов комбинаторных множеств справедливо следующее соотношение:

N(С(А(а₁  а₂  …  a_p))) = N(С(А(а₁ = а₂ = … = а_p)))  p!.

Аналогично рассмотрим все варианты расположения некоторого множества объектов A на заданном множестве мест М, содержащем выделенное подмножество из s мест {m} = {m₁, m₂, …, m_s} ({m}  M). Обозначим через C(А(m₁  m₂  …  m_s)) комбинаторное множество, образованное из A при условии различия всех s мест в подмножестве {m}, а через C(А(m₁ = m₂ = … = m_s)) – аналогичное множество вариантов расположения, полученное из A при условии неразличимости всех мест в {m}.

Для общих чисел различных вариантов расположения объектов в двух рассмотренных случаях справедливо аналогичное соотношение

N(С(А(m₁  m₂  … m_s))) = N(С(А(m₁ = m₂ = … = m_s)))  s!

Справедливость обеих формул вытекает из того, что каждому варианту расположения p неразличимых объектов (соответственно, объектов на s неразличимых местах) по правилу умножения соответствует p! разных вариантов перестановок при различающихся объектах (соответственно, s! разных вариантов перестановок при различающихся выделенных местах). Введенное правило комбинаторики назовем правилом учета сходства-различия. Расчетная схема для учета сходства-различия объектов приведена на рис. 5.5.

1. 
   Рис. 5.5. Расчетная схема для учета сходства-различия объектов
   

Для обратного перехода от расположения различных объектов к расположению одинаковых предложено использовать обратную стрелку, которая обозначает не умножение на следующее число, а деление на него. Расчетная схема такого перехода для учета сходства-различия объектов дана на рис. 5.6.



Рис. 5.6. Расчетная схема обратного перехода в правиле учета сходства-различия