Проектирование привода ленточного транспортера. Имени академика М. Ф. Решетнева
 Скачать 1.37 Mb. Скачать 1.37 Mb.
|
Расчет цилиндрических зубчатых передачВыбор материала передачи Расчет выполняем для прямозубой цилиндрической передачи редуктора, тихоходный вал которого нагружен вращающим моментом Т2 = 927,52 Н·м. В соответствии с рекомендациями прямозубой передачи и вращающем моменте материал колес передачи занесем в таблицу 2.1: Таблица 2.1 - Материал и твердость колеса и шестерни
Допускаемые напряжения Допускаемые контактные напряжения Определяем допускаемые контактные напряжения по формуле 2.1 с учетом рекомендаций [1;25] [σ] = σН ∙  (2.1) Н 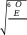 где: KHL – коэффициент долговечности где: KHL – коэффициент долговечности𝐿 𝐿 = ≥ 1 (2.2)  где: NHE – число циклов нагружений 𝐿 = 60𝐿ℎ (2.3) где: n – частота вращения (шестерни или колеса), мин-1; Lh – общее время работы передачи, ч 𝐿ℎ = ∙ 365дней ∙ Кгод∙ 24 ч ∙ Ксут (2.4)
где: Т – срок службы передачи, лет; Кгод – коэффициент использования передачи в течение года; Ксут – коэффициент использования передачи в течение суток Допускаемое контактное напряжение для шестерни: [σ] = 17 HRCср+ 200 ∙  = 17 ∙ 52 + 200 ∙ 1,0 = 903МПа  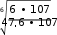 Н1 Н1 𝐿 1,2 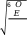 𝐿 = = 𝐿 = == 0,708 < 1 Исходя из расчетов, коэффициент долговечности получился меньше единицы, в таком случаи, принимаем его равным 1,0 𝐸 = 60𝐿ℎ = 60 ∙ 300,04 ∙ 26490,24 = 476 887 896,58 = 47,6 ∙ 107 𝐿ℎ = 6 ∙ 365 ∙ 0,70 ∙ 24 ∙ 0,72 = 26490,24 Допускаемое контактное напряжение для колеса: [σ] = 17 HRCср+ 200 ∙  = 17 ∙ 48 + 200 ∙ 1,0 = 846МПа  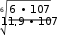 Н2 Н2 𝐿 1,2 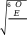 𝐿 = = 𝐿 = == 0,892 < 1  Исходя из расчетов, коэффициент долговечности получился меньше единицы, в таком случаи, принимаем его равным 1,0 𝐸 = 60𝐿ℎ = 60 ∙ 75 ∙ 26490,24 = 119 206 080 = 11,9 ∙ 107 𝐿ℎ = 6 ∙ 365 ∙ 0,70 ∙ 24 ∙ 0,72 = 26490,24 Допускаемое напряжение для расчета передачи будет следующим: [σ]Н = [σ]2 = 846МПа
Допускаемые напряжения на изгиб Допускаемые напряжения изгиба для расчетов на прочность при длительной работе в постоянном режиме нагружения вычисляем раздельно для шестерни и колеса по зависимостям, аналогичным формулам для определения допускаемых контактных напряжение: σ = σF ∙ ∙  (2.5) 𝐿 𝐶 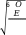 где: KFL – коэффициент долговечности для закаленных зубчатых колес где: KFL – коэффициент долговечности для закаленных зубчатых колес𝐿 = ≥ 1 (2.6) 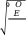 где: KFL – коэффициент долговечности для улучшенных зубчатых колес где: KFL – коэффициент долговечности для улучшенных зубчатых колес𝐿 = ≥ 1 (2.7) Базовое число циклов нагружений NFO = 4∙106 Число циклов нагружений NFЕ за весь срок службы передачи, вычисляем так же, как и при расчетах аналогичным напряжением NHЕ Допускаемое напряжение на изгиб для шестерни: [σ]1 = 680 ∙ 1,0 ∙ 1,0 = 400МПа  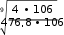 1,7 1,7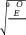 𝐿 = = 𝐿 = == 0,588 < 1  Исходя из расчетов, коэффициент долговечности получился меньше единицы, в таком случаи, принимаем его равным 1,0 𝐸 = 60𝐿ℎ = 60 ∙ 300,04 ∙ 26490,24 = 476 887 896,58 = 476.8 ∙ 106 𝐿ℎ = 6 ∙ 365 ∙ 0,70 ∙ 24 ∙ 0,72 = 26490,24 𝐿 = 1.0 Допускаемое напряжение на изгиб для колеса:
[σ]2 = 620 ∙ 1,0 = 364МПа  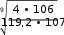 1,7 1,7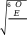 𝐿 = = 𝐿 = == 0,685 < 1 Исходя из расчетов, коэффициент долговечности получился меньше единицы, в таком случаи, принимаем его равным 1,0 𝐿 = 60𝐿ℎ = 60 ∙ 75 ∙ 26490,24 = 119 206 080 = 119,2 ∙ 106 𝐿ℎ = 6 ∙ 365 ∙ 0,70 ∙ 24 ∙ 0,72 = 26490,24 𝐿 = 1,0 Сведем полученные допускаемые напряжения в таблицу 2.2 Таблица 2.2 – Механические свойства выбранных материалов колес
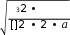 Проектный расчет закрытой цилиндрической зубчатой передачи По условию контактной прочности определяем межосевое расстояние, мм: Проектный расчет закрытой цилиндрической зубчатой передачи По условию контактной прочности определяем межосевое расстояние, мм: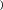 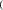 где: где:𝑎 = 𝑎 ± 1 ∙ , (2.8) Ka – коэффициент межосевого расстояния (для прямозубых колес, Ka =495); u – передаточное отношение; Т2 – крутящий момент на валу колеса, Н∙м; Ψba – коэффициент ширины колеса b2 относительно межосевого расстояния aω; KHβ – коэффициент неравномерности ораспределения нагрузки по контактной линии; [σ]Н – допускаемое контактное напряжение, МПа. 𝑎 = 495 ∙ 4,0 + 1 ∙ 3 927,52 ∙ 1,07 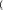 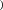  [846,5]2 ∙ 4,02 ∙ 0,325 [846,5]2 ∙ 4,02 ∙ 0,325=2475 ∙ 0,064 = 158,40 мм 
  = ∙ ( + 1) = 0,325 ∙ (4 + 1) = 0,8125 (2.9) 𝑎 2 2 Из стандартного ряда выбираем ближайшее значение 𝑎 = 160 мм Для прямозубых колес модуль зацепления, мм определяется как:  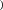 = 0,01…0,02 ∙ 𝑎 = 0,015 ∙ 160 = 2,4 (2.10) = 0,01…0,02 ∙ 𝑎 = 0,015 ∙ 160 = 2,4 (2.10)Из стандартного ряда, выбираем ближайшее значение для нашего модуля m = 2,5. Определим суммарное число зубьев zc, для прямозубых колес определяется по формуле:   = 2𝑎 = 2 ∙ 160 = 128 (2.11) 2,5 Вычисляем число зубьев шестерни z1 и колеса z2 по формуле:  1 = + 1 = 128  4 + 1 4 + 1= 25,6 (2.12)  Полученное значение округляем до целевого числа. Для лучшей приработки колес, число зубьев шестерни рекомендуется принимать нечетным. Таким образом, количество зубьев на шестерни будет 25. Полученное значение округляем до целевого числа. Для лучшей приработки колес, число зубьев шестерни рекомендуется принимать нечетным. Таким образом, количество зубьев на шестерни будет 25.1 = 25, − 1 = 128 − 25 = 103 (2.13) Уточняем передаточное число отношение: = 2 = 103 = 4,12   1 25 Отклонение от заданной величины составляет:  ∆ = 4,12 − 4,0 ∙ 100% = 3% (2.14) ∆ = 4,12 − 4,0 ∙ 100% = 3% (2.14)4,0 Расхождение величины u с исходными передаточным числом передачи не должно превышать ±4%. В нашем случаи, расхождение величины не превышает указанного.
Геометрические размеры колес находим согласно формулам, приведенным в [1;30] Таблица 2.3 – Основные геометрические параметры передач внешнего зацепления с цилиндрическими колесами
  Затем вычисляем окружную скорость колес: Затем вычисляем окружную скорость колес:  = ∙ 1 ∙ 1 = 3,14 ∙ 62,5 ∙ 300,04 = 0,98 м/с (2.15) 1 60 ∙ 1000 60 ∙ 1000 или   = ∙ 2 ∙ 2 = 3,14 ∙ 257,5 ∙ 75 = 1,01 м/с 2 60 ∙ 1000 60 ∙ 1000  Исходя из расчетной скорости колес, выбираем 9 степень точности изготовление передачи
Проверочный расчет закрытой цилиндрической зубчатой передачи Таблица 2.4 – Силы, действующие в зацеплении цилиндрических передач     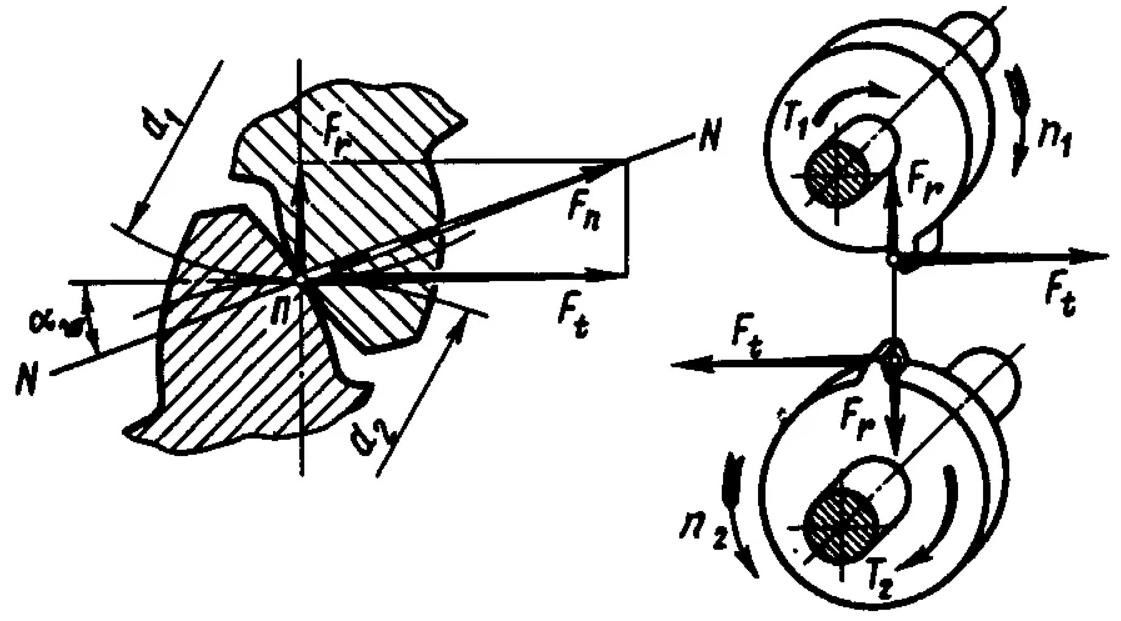 Покажем рассчитанные силы, действующие на зубья на рисунке 2.1 Покажем рассчитанные силы, действующие на зубья на рисунке 2.1Рисунок 2.1 – Действующие силы в зацеплении Проведем проверку зубьев на контактную прочность. Расчетные контактные напряжения определяем по формуле: = ∙ ∙ ∙ ≤ σ (2.16) 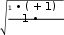 где: где:Н Н М 
ZH = 1,76 ∙ cos β – коэффициент, учитывающий форму сопряжения зубьев; ZМ = 275 МПа1/2 – коэффициент, учитывающий материал передачи; 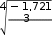 Zἐ - коэффициент, учитывающий суммарную длину контактной линии, для прямозубых колес: Zἐ - коэффициент, учитывающий суммарную длину контактной линии, для прямозубых колес: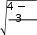 = = = == 0,872 (2.17) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
