Информационные технологии для менеджеров - Грабауров В. А.. Информационные
 Скачать 18.31 Mb. Скачать 18.31 Mb.
|
3.2. Использование статистических пакетов для ответов на вопросы
Можно поставить множество вопросов, которые интересны менеджеру, и ответ на них попытаться найти при помощи обработки статистических данных. Рассмотрим примеры поиска ответов на вышеперечисленные вопросы с помощью распространенных универсальных статистических пакетов Statistica for Windows и Statgraphics. Куда движется фирма? Построение тренда (направленности) В окружающей нас внешней среде имеется огромное количество явлений и объектов, изменяющихся в пространстве и во времени, и любой набор данных, состоящий из упорядоченных по этим координатам измерений, может рассматриваться как динамический ряд. Жизнь идет, со временем меняются показатели работы фирмы. Чтобы выявить тенденции их изменений, выделим из набора данных направленность (тренд), т.е. постепенное изменение за длительное время или на больших расстояниях. Наиболее эффективным методом описания тренда является подбор некоторого аналитического выражения, как правило, полинома невысокой степени. Более высокая степень полинома или другая нелинейная зависимость нуждается в смысловом обосновании. Нахождение уравнений тренда осуществим методом регрессионного анализа. В качестве примеров использования статистических расчетов рассмотрим обработку макроэкономических показателей США за 1930-1990 гг. из пакета MACRO. Представим себе, что сейчас 1980 г., и попытаемся предсказать валовой национальный продукт (GNP) в 1990 г. На рис. 3.1 показаны результаты обработки данных по валовому национальному продукту США (GNP) за 1930-1980 гг. Подставив Years(x) = 1990 в расчет ожидаемого GNP в 1990 г., получим GNPpacч(y)= 4111,8. Если сравнить с реальным GNP = 4156,0, то увидим, что ошибка предсказания составляет около 1%! Естественно, далеко не всегда можно предсказывать будущее с такой точностью, но все же этот пример свидетельствует о полезности метода. Аналогичные расчеты можно провести для вашей фирмы. Данный пример выполнен в пакете Statistica (о нем ниже), но подобные вычисления можно сделать в различных универсальных или специальных статистических пакетах. 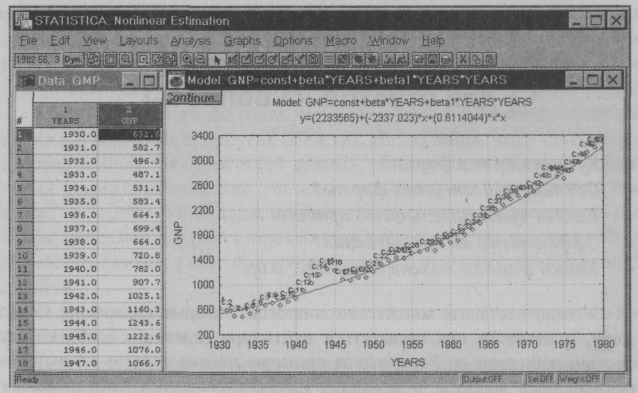 Рис.3.1. График линии регрессии (тренда) и исходные данные От чего зависит успех фирмы? Многомерный факторный анализ Большинство объектов, в том числе и ваша фирма, как правило, подвержены влиянию сразу множества воздействий. Реально затруднительно контролировать и управлять всеми ими, т.е. объекты являются частично управляемыми и наблюдаемыми. Следовательно, при разработке методов управления экономическими объектами приходится решать, какие воздействия необходимо измерять, включать их в математические модели и далее учитывать в первую очередь, а какими можно в крайнем случае пренебречь. Задача определения степени влияния воздействий (наблюдаемых параметров) на выходной параметр объекта управления (например, прибыль фирмы, уровень зарплаты и т.д.) решается с помощью многомерного факторного анализа по доле дисперсии выходного параметра. Полная дисперсия выходной переменной у может быть разбита на три основных компонента: 1) общую дисперсию, которую можно определить как часть дисперсии переменной у, появляющейся под действием исследуемых воздействий; 2) специфическую дисперсию, представляющую собой часть, которая не связана с измеренными переменными, а обусловлена влиянием неизмеряемых воздействий; 3) дисперсию, обусловленную ошибкой измерения. Она является случайной, вызванной ошибками в процессе выборки, отклонениями от условий эксперимента и т.д. Полная (нормированная) дисперсия переменной у равна 1, а все составляющие дисперсии в правой части уравнения представляют доли в полной дисперсии: где i = 1; Sy2 - специфическая дисперсия; Zy2 - дисперсия, обусловленная ошибкой измерения. Отсюда следует, что квадраты факторных нагрузок показывают доли дисперсии измеряемого показателя, в том числе выходного параметра, приходящиеся на соответствующие факторы. На основе матрицы наблюдений с помощью процедуры многомерного факторного анализа (Factor Analysis) строится матрица факторных нагрузок. Эта матрица позволяет проранжировать исходные переменные по степени влияния на исследуемую переменную. В качестве примера рассмотрим, какие макроэкономические показатели в наибольшей степени влияют на зарплату (Wages) американцев. Исходные статистические данные возьмем из пакета Macro, а расчет методом факторного анализа (Factor Analysis) выполним в пакете Statistica. Оценим степень влияния переменных Years (годы), GNP, Inflation Rate (уровень инфляции), Real Net Export (реальный чистый экспорт), Unemployment Rate (уровень безработицы) и Exchange Rate (валютный курс) на Wages (заработную плату). Здесь среди экономических показателей присутствует показатель "годы", который несет в себе в неявном виде изменения, происходящие с исследуемым объектом с течением времени, например, научно-технический прогресс, компьютеризация и т.д. На рис. 3.2 показана матрица факторных нагрузок, из анализа которой можно сделать следующие выводы. На переменную Wages основное влияние оказывает первый фактор (Factor 1). Рассмотрим наполненность этого фактора переменными (первая колонка). Помимо самой Wages, которая характеризует специфическую дисперсию и ошибку измерений, на заработную плату более других влияют GNP и Years. 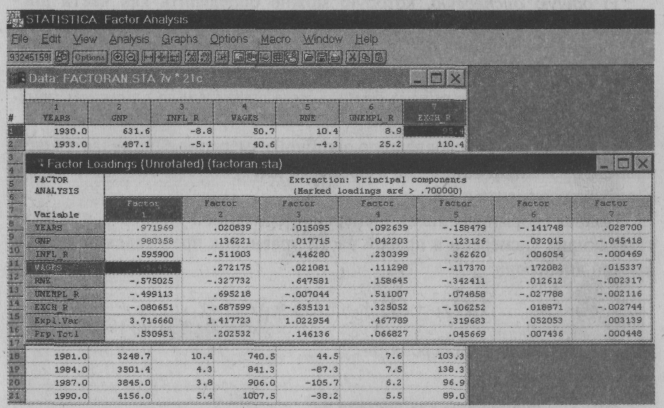 Рис. 3.2. Окно Factor Analysis Какова чувствительность прибыли (зарплаты) к ...? По результатам факторного анализа мы выяснили, что на зарплату американцев наибольшее влияние оказывают годы и GNP. Построим математическую модель зависимости зарплаты от GNP и лет. Для нахождения параметров многомерных регрессионных моделей используем тот же математический аппарат, который применялся для построения тренда, а в качестве исходных данных - статистические показатели из MACRO. Квадратичную трехмерную модель с помощью процедуры Nonlinear Estimation (нелинейная обработка) построим по формуле где z - Wages; х - GNP; у - Years. Построенная в программе Statistica модель и ее поверхность отклика показаны на рис. 3.3. Имея модель, мы можем поставить различные вопросы. Например, если GNP США в 1990 г. возрос бы на 10%, то насколько увеличилась бы зарплата американцев? Если тоже на 10% или более, то это означает, что американцы живут в значительной степени для себя, а не только для "светлого будущего". Фактически таким образом мы ставим вопрос о чувствительности обобщенного показателя (зарплаты, прибыли и т.д.) к изменению исходных параметров. 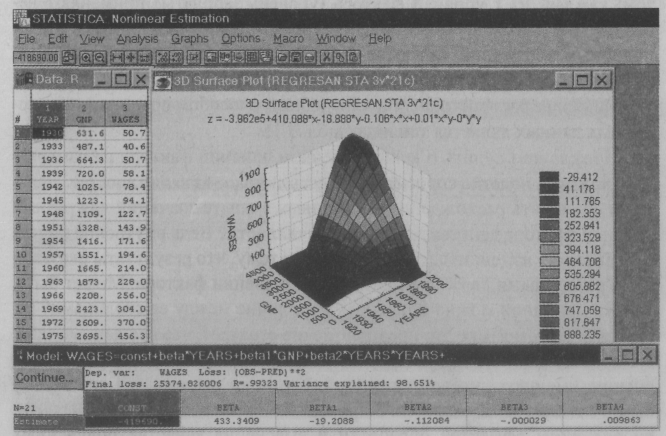 Рис. 3.3. Поверхность отклика трехмерной модели Эффективны ли нововведения? Однофакторный анализ При исследовании зависимостей одной из наиболее простых является ситуация, когда можно указать только один фактор, влияющий на конечный результат, и этот фактор может принимать лишь конечное число значений (уровней). Такие задачи (называемые задачами однофакторного анализа) довольно часто встречаются на практике. Типичный пример задач однофакторного анализа - сравнение по достигаемым результатам нескольких различных способов действия (обработок), направленных на достижение одной цели (например, повышение зарплаты или нескольких видов рекламы и т.д.). Для сравнения влияния факторов на результат необходим определенный статистический материал. Обычно его получают следующим образом: каждый из kуровней фактора (уровень зарплаты) применяют несколько раз к исследуемому объекту и регистрируют результаты. Итогом подобных испытаний являются kвыборок (производительности труда различных рабочих при разных уровнях зарплаты). Наиболее распространенным и удобным способом представления подобных данных является таблица (табл. 3.1). Прежде чем судить о количественном влиянии фактора на измеряемый признак, полезно спросить себя, есть ли такое влияние вообще. Нельзя ли объяснить расхождения полученных в опыте значений для разных уровней фактора действием чистой случайности? Ведь внутренне присущая явлению изменчивость уже привела к тому, что результаты оказываются различными даже при неизменном значении фактора. Может быть, той же причиной можно объяснить и различие между ее столбцами? На статистическом языке это предположение означает, что все данные табл. 3.1 принадлежат одному и тому же распределению. Это предположение обычно именуют нулевой гипотезой. Если оно оказывается справедливым, то анализ заканчивается. В противном случае возникает задача оценки величины эффектов обработки и выяснения качества полученных оценок. Таблица 3.1 Результаты испытаний влияния уровня заработной платы на производительность труда
Внутри каждой колонки имеются различные результаты, так как производительность труда зависит не только от зарплаты, но и от других факторов, о которых мы можем даже не знать. Задачей однофакторного анализа является определение, значимо ли влияние исследуемого фактора. Проиллюстрируем применение описанных выше критериев на следующем примере [3]. Для выяснения влияния денежного стимулирования на производительность труда шести однородным группам из пяти человек каждая были предложены задачи одинаковой трудности. Задачи предлагались каждому испытуемому независимо от всех остальных. Группы отличались между собой величиной денежного вознаграждения за решаемую задачу. 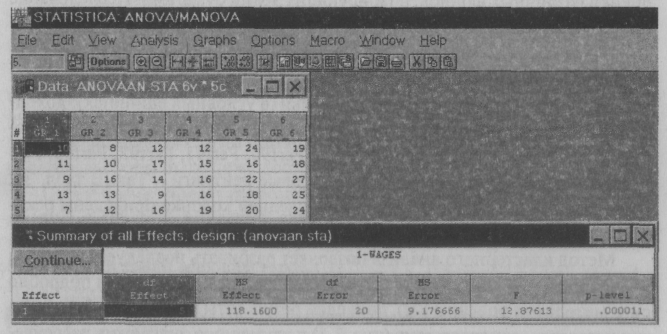 Рис. 3.4. Результирующая таблица однофакторного анализа В качестве нулевой гипотезы примем предположение об отсутствии влияния денежного вознаграждения на число решенных задач и проверим эту гипотезу. Исследование проведем в программе Statistica методом ANOVA/MANOVA. Сокращение ANOVAпроисходит от выражения "Analysis of variance". В отечественной литературе вместо термина "анализ вариации" чаще используется термин "дисперсионный анализ". Результаты анализа представлены на рис. 3.4. Для данных нашего примера из приведенной таблицы дисперсионного анализа можно сделать вывод, что нулевая гипотеза об отсутствии эффектов обработки должна быть отвергнута, так как вероятность получения указанного или большего значения F-отношения (уровень значимости F-статистики) при нулевой гипотезе (p.level) значительно меньше допустимого уровня риска 0,05. Таким образом, фактор "денежное стимулирование" влияет на производительность труда. Каким фирмам можно доверять? Кластерный анализ Еще одна интересная и часто встречающаяся задача связана с классификацией объектов. Эта задача неоднозначна, и для ее решения применяются методы многомерного анализа, основанные на группировке схожих объектов, такие, как кластерный и дискриминантный анализы. В качестве примера рассмотрим задачу о рынке ценных бумаг, в частности проблему оценки различных фондов, оперирующих этими бумагами. Исследование проведем методом кластерного анализа в пакете Statgraphics. В рассматриваемом примере [2] будут исследованы 16 известных инвестиционных фондов для оценки их состояния. В качестве переменных используются следующие характеристики (в условных единицах): доходность за пятилетний период - Five- Yr, риск - Risk, ежегодный процент дохода (performance) для каждого года – Perf90, Perf91, Perf92, Perf93, Per-f94, расходная часть - Expense и налоговые рейтинги - Tax. В табл. 3.2 приведены исходные данные, а в ее последней колонке приведены рекомендации экспертов. Метод кластерного анализа позволяет разбивать исследуемые фонды на группы в зависимости от степени их близости. Не описывая подробно сути метода (он описан в [2]), приведем результаты разделения фондов на три кластера - дендрограмму (рис. 3.5) и двумерную диаграмму рассеивания (рис. 3.6). Таблица 3.2 Данные об инвестиционных фондах
Помимо графического представления разделения исследуемых фондов на группы метод кластерного анализа дает количественные оценки, позволяющие прийти к выводам о целесообразности инвестиций. В частности, в первом кластере видно, что расходы были разумными: несмотря на низкие доходы в 1990 г., заметно, что в других годах состояние фондов первого кластера постоянно улучшалось. Также в первом кластере индицируется самый низкий рейтинг риска среди всех кластеров, а налоговые сборы были тоже достаточно невысокими. Переменные, представляющие кластер 2, говорят о том, что здесь имелись наибольшие расходы, хотя за пятилетний период доходы оставались самыми высокими. Оценка риска и налоговые сборы являются максимальными среди всех кластеров. О третьем кластере можно сказать, что он занимает второе место по расходам относительно доходов за пятилетний период. Оценка риска была самая высокая, однако налоговые сборы существенно ниже, чем у первого кластера. 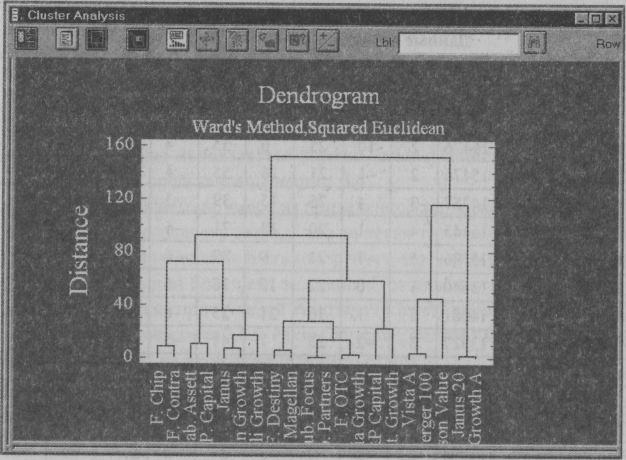 Рис. 3.5. Дендрограмма для грех кластеров 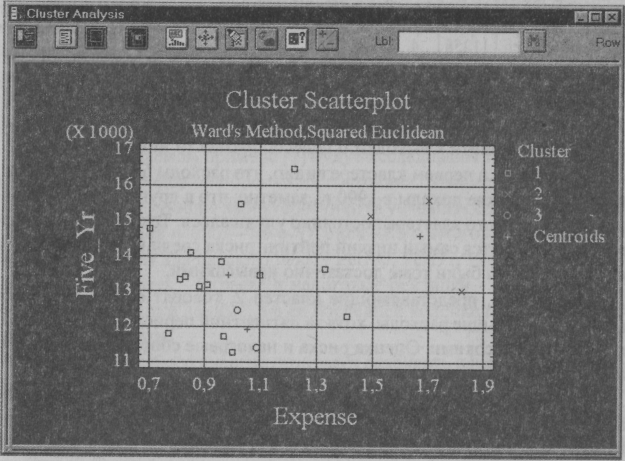 Рис. 3.6. Двумерная диаграмма рассеивания Рекомендации по действиям с акциями: покупка (Buy), удержание (Hold) и продажа (Sell) выполнены методом дискриминантного анализа. Результаты этой классификации близки результатам кластерного анализа. Расхождение наблюдается только в одном случае из 16. |
