ВКР Сотина. Исследование фазовых эффектов и методов разделения азеотропных смесей, утверждена приказом ргу имени С. А. Есенина от 20 г
 Скачать 1.21 Mb. Скачать 1.21 Mb.
|
1.2. Законы описывающие термодинамические состояния азеотропных смесейПравило фаз Гиббса Состояние системы определяется температурой, давлением, концентрацией компонентов в разных фазах. При изменении этих факторов система переходит из одного состояния в другое, при этом совершаются фазовые превращения, при которых появляются новые фазы или исчезают старые. Возможность изменения равновесного состояния системы определяется вариантностью или числом степеней свободы. Число факторов, которые могут изменяться независимо друг от друга, без нарушения равновесия системы, называется числом степеней свободы. Вариантность системы зависит от числа компонентов, числа равновесных фаз и количества внешних переменных. Эта зависимость была получена в 1876 г. Гиббсом и носит название правила фазГиббса. Для вывода правила фаз Гиббса рассмотрим систему, содержащую К компонентов, в которой образуется Ф фаз. Внешними переменными являются температура и давление. Пусть каждая фаза содержит все К компонентов. В качестве переменных, определяющих состояние системы, выступают концентрации всех компонентов во всех фазах. Число таких переменных будет равно произведению КФ. С учетом внешних переменных, получаем общее число переменных, равное КФ + 2. Пусть при любой температуре все фазы находятся в равновесии друг с другом. Это возможно при равенстве химических потенциалов компонентов во всех фазах, т.е. химический потенциал каждого компонента одинаков во всех фазах. Это условие можно записать в виде следующих равенств: µ11 = µ21 = µ31 = .... = µj1 µ12 = µ22 = µ32 = .... = µj2 (17) µ1K = µ2K = µ3K =.... = µjK где µ – химический потенциал, верхний индекс – номер компонента, нижний индекс – номер фазы. В каждой строке равенства (17) (Ф–1) самостоятельных уравнений, число строк равно К, следовательно всего таких уравнений будет К(Ф–1). К ним следует добавить еще Ф уравнений, связывающих концентрации всех компонентов во всех фазах. Следовательно, общее число уравнений, связывающих все переменные будет (Ф–1)К+Ф [27]. Если число переменных больше числа связывающих их уравнений, то не все переменные являются независимыми. Число независимых переменных определяется как разность общего числа переменных и числа уравнений, т.е. f= КФ + 2 – ((Ф – 1)К + Ф) = К – Ф + 2 (18) Выражение (18), определяющее вариантность системы, – правило фаз Гиббса, f - число степеней свободы системы. На практике процессы идут при постоянном давлении, поэтому правило фаз Гиббса запишется в виде: f = К– Ф + 1 (19) Из вывода правила фаз Гиббса следует, что число степеней свободы всегда положительно или равно нулю (f < 0 соответствовало бы случаю, когда число уравнений было бы больше числа переменных, а такая система уравнений несовместна). [26] Если f = 0 (система называется нонвариантной), то все независимые переменные, определяющие состояние системы, имеют строго фиксированные (единственные) значения, которые нельзя изменить, не нарушив фазового равновесия системы. Наличие одной, двух или большего числа степеней свободы позволяет независимо изменять одну, две или большее число переменных без изменения числа фаз, находящихся в равновесии. Правило фаз широко используется как при изучении диаграмм состояния, так и при их построении, что будет показано ниже. Законы Коновалова Законы Коновалова устанавливают связи между изменениями состава и давления (при T= const), состава и температуры (при Р = const) в бинарных двухфазных системах и лежат в основе теории процессов перегонки и ректификации бинарных смесей. Законы действуют при P = const или T = const. Они действуют в условиях изменения одной переменной (при P = const или T = const ) и устанавливают связь между изменениями составов фаз и давлением (температурой), т.е. описываются частными формами уравнения Ван-дер-Ваальса. Первый закон Коновалова. Первый закон Коновалова относится к азеотропным точкам. Преобразуем частные формы уравнения Ван-дер-Ваальса (20) и (21): Vжп 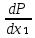 = (y1 - x1) = (y1 - x1) 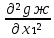 (20) (20)-Sжп 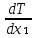 = (y1 - x1) = (y1 - x1) 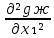 (21) (21)В точке азеотропа составы фаз равны: y1аз= х1аз, т.е. у1- х1 = 0. Вторая производная 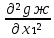 - конечная величина, знак которой определяется типом экстремума зависимостипотенциала от состава. Для устойчивых фаз эта величина всегда положительна. - конечная величина, знак которой определяется типом экстремума зависимостипотенциала от состава. Для устойчивых фаз эта величина всегда положительна.При фазовом переходе жидкостьпар объем и энтропия системы увеличиваются: Vn >Vж на величину изменения объема при испарении; Sn>Sж на величину энтропии испарения, т.е. Sжп, Vжп характеризуются положительным конечным значением [31]. Следовательно, равенства (20) и (21) будут выполняться только при 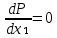 и и 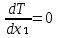 , что соответствует наличию экстремума на зависимостях давления (Р) x-y и температуры (T) x-y. , что соответствует наличию экстремума на зависимостях давления (Р) x-y и температуры (T) x-y.Приведем две формулировки закона Коновалова: - если давление (либо температура) сосуществования двух бинарных фаз имеют экстремум (максимум или минимум), то фазы имеют одинаковые составы; - вдоль изотермы (изобары) в азеотропной точке наблюдается экстремум на зависимости. 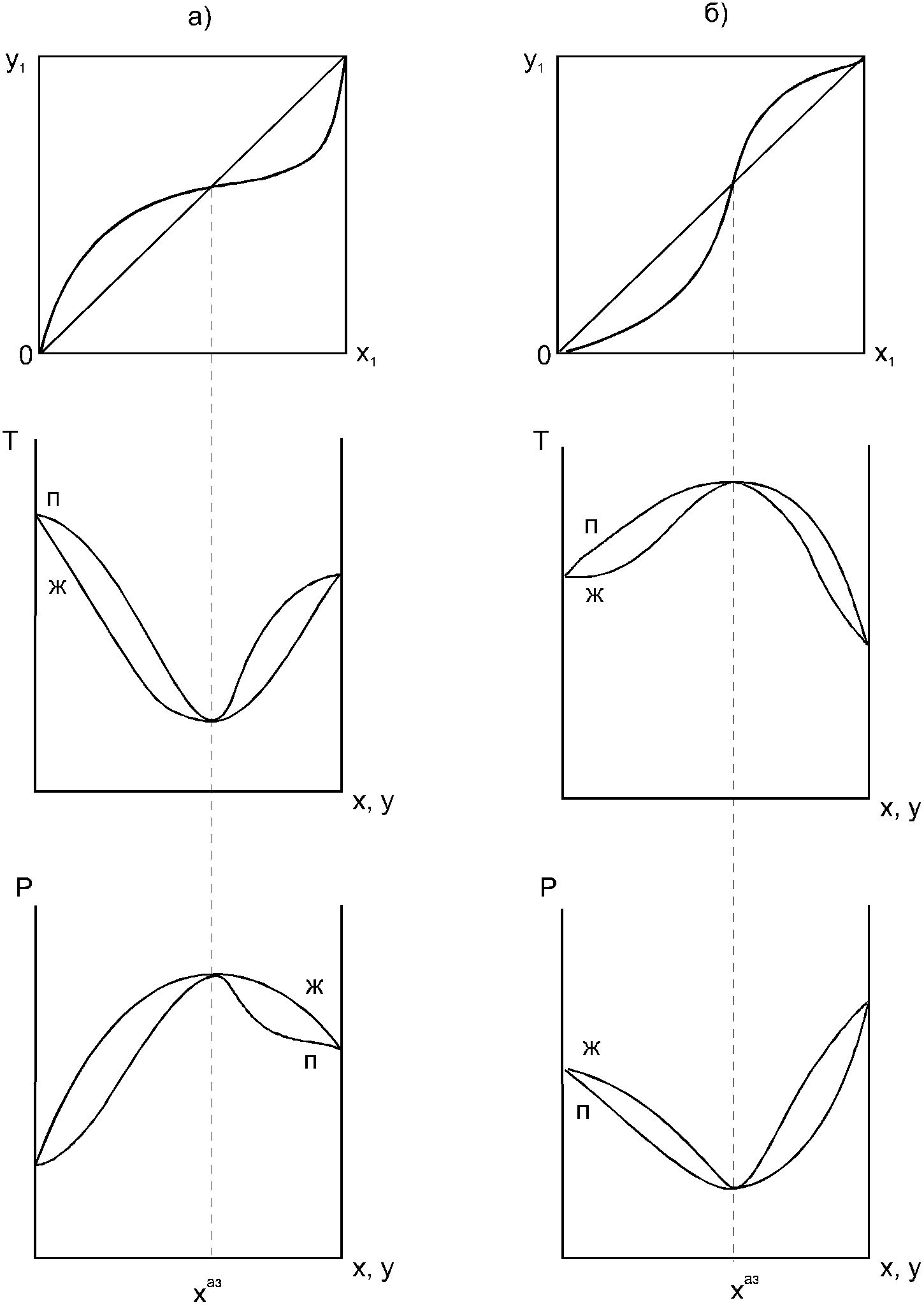 Рис. 1. Диаграммы фазового равновесия жидкостьпар гомогенных азеотропных систем: а - положительный азеотроп, б - отрицательный азеотроп. Рис. 1 может служить графической иллюстрацией данного закона. Если бинарная смесь имеет точку, которая характеризуется равенством составов паровой и жидкой фаз, то на концентрационных зависимостях при постоянной температуре (при постоянном давлении) этому составу отвечает экстремальное значение давления (температуры). Следует уделить внимание тому факту, что экстремумы являются относительными, т.к. реализуются при определенных закрепленных условиях. Азеотропные данные (состав, температура, давление) являются необходимой информацией при разработке принципиальных технологических схем разделения бинарных и многокомпонентных смесей. Они публикуются в периодической физико-химической литературе, а также приводятся в специальных справочниках. Вывод о наличии либо отсутствии азеотропа можно сделать и при анализе экспериментальных данных о ПЖР. Однако чаще всего точные азеотропные параметры в наборах данных не приводятся (табл.1,2). В этом случае необходимо соответствующим образом обработать экспериментальную информацию, руководствуясь следствием из первого закона Коновалова. [4] Следствие из первого закона Коноваловаотносится к характеру хода зависимости коэффициентов распределения компонентов от состава ki(x1) вблизи азеотропа: в окрестности особой точки (dk1/dx1)<0 для положительного азеотропа и (dk2/dx1)>0 для отрицательного. Таблица 1.Данные парожидкостного равновесия в системе этанол (1) –вода (2)
Таблица 2. Парожидкостное равновесие в системе вода (1) –муравьиная кислота (2) при 50 мм рт. ст.
Второй закон Коновалова. Второй закон Коновалова справедлив для всех точек, исключая азеотропные и точки чистых компонентов. Рассмотрим частные формы уравнения Ван-дер-Ваальса (5) и (6) при различных соотношениях составов паровой и жидкой фаз. Учтем приведенный выше анализ знаков величин, входящих в уравнения. Если y1> x1 , то при Т=const 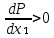 ; при Р=const ; при Р=const 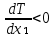 . .Если y1< x1 , то при Т=const 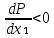 ; при Р=const ; при Р=const 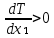 . .Дадим объединенную формулировку второго закона Коновалова для изобарических (изотермических) условий: пар по сравнению с жидкостью обогащен тем компонентом, добавление которого в жидкую фазу ( dx1>0) понижает ее температуру кипения dT<0 (повышает давление над раствором dP>0). Графическая интерпретация закона для зеотропных смесей представлена на рис. 2. 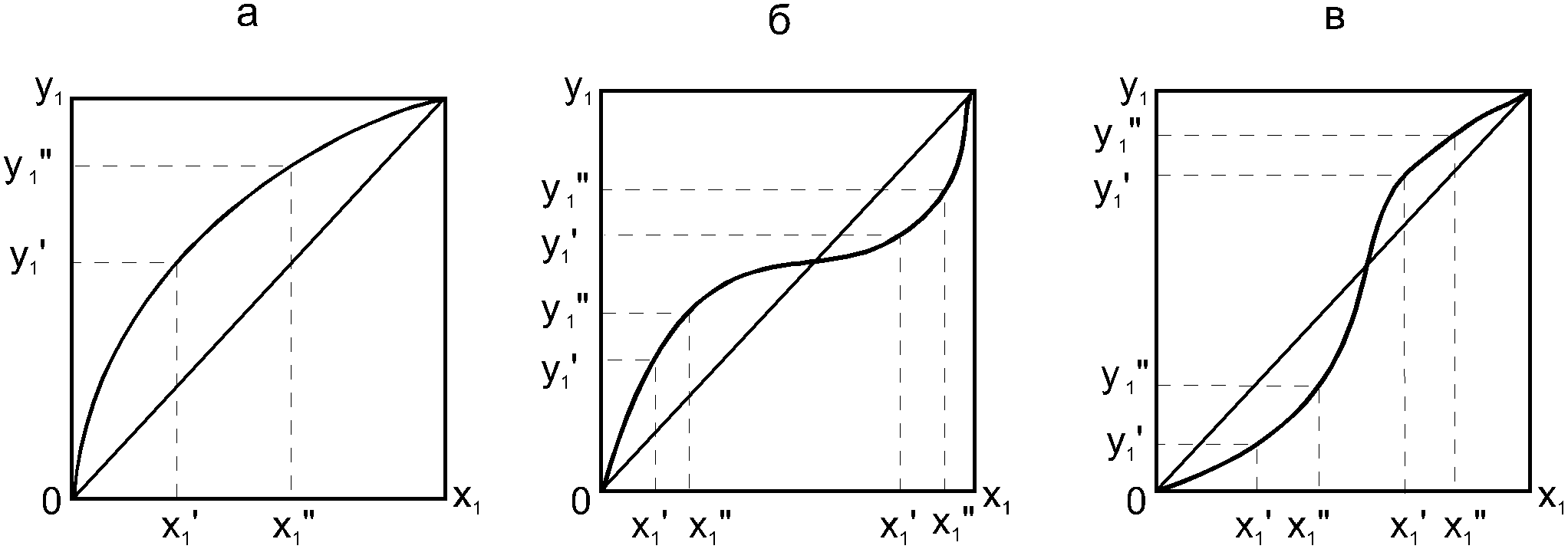 Рис. 2. Графическая интерпретация третьего закона Коновалова: а - зеотропная смесь; б, в - азеотропные системы. Как видно, пар по сравнению с жидкостью обогащен первым компонентом – компонентом, при добавлении которого к жидкой фазе (х1">х1') температура вдоль изобары уменьшается (Т" < Т'), а давление вдоль изотермы повышается (Р" > Р'). В таблице 1 приведены экспериментальные данные ПЖР, позволяющие проиллюстрировать закон Коновалова на примере системы с положительным азеотропом. Рассмотрим данные при 70 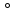 С (х1аз 90 мольн. %). Для области составов жидкой фазы 0 С (х1аз 90 мольн. %). Для области составов жидкой фазы 0Доказательство второго закона Коновалова: Согласно уравнению Дюгема-Маргулеса, которое описывает равновесие в идеальных бинарных растворах газов или давление насыщенного пара над идеальным бинарным жидким раствором (1 - x) dlnp1= -xdlnp2 (22) или (1-x) 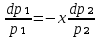 (23) (23)где x — мольная доля второго компонента в растворе, p1 и p2 — парциальные давления первого и второго компонента [53]. Отсюда следует, что dp1= 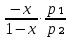 dp2 (24) dp2 (24)По закону Дальтона p2 = yp (25) p1 = (1-y)p (26) где (1-y) и y — мольные доли первого и второго компонента в насыщенном паре, p — общее давление в системе. Тогда: dp1= 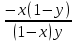 dp2 (27) dp2 (27)Поскольку общее давление есть сумма парциальных, то dp = dp1 + dp2. Подставив в это выражение значение dp1 из предыдущего получим dp= 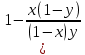 )dp2 (28) )dp2 (28)Разделив обе части на dx и раскрыв скобки получим, что 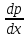 = =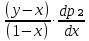 (29) (29)В экстремуме dp/dx = 0, следовательно 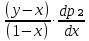 = 0 (30) = 0 (30)Поскольку dp2/dx > 0, так как с ростом концентрации второго компонента растёт и его парциальное давление, то равенство может соблюдаться только если x = y — когда состав пара и раствора одинаков, что и доказывает второй закон Коновалова. Растворы, состав которых отвечает точке экстремума, кипят при постоянной температуре, а их состав при перегонке не изменяется. Такие растворы называются «азеотропными растворами» или «азеотропами». Разделение азеотропов методом фракционной перегонки невозможно. Для разделения таких растворов используют химические методы, перегонку с третьим компонентом либо фракционную перегонку при другом давлении [12]. Третий закон Коновалова. Запишем для фазовых переходов, соответственно жидкость пар и пар жидкость в изобарических условиях частные формы уравнения Ван-дер-Ваальса: -Sжп 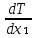 = (y1 - x1) = (y1 - x1) 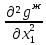 dx1, (31) dx1, (31)-Sпж 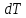 = (x1 - y1) = (x1 - y1) 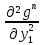 dy1 (32) dy1 (32)После преобразования получим: 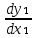 = = 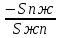 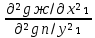 (33) (33)В силу устойчивости фаз вторые производные потенциала положительны. Знаки и Sжп противоположны. Следовательно, dy1/ dx1 > 0. Третий закон Коновалова формулируется следующим образом: составы равновесных паровой и жидкой фаз в изотермических и изобарических условиях изменяются однонаправленно (симбатно). На рис. 2 представлена графическая интерпретация данного закона. Независимо от типа системы при увеличении содержания первого компонента в жидкой фазе (х''1>x'1) увеличивается его концентрация в паре (y1''>y1'). Действие 3-го закона Коновалова можно проиллюстрировать и табличными экспериментальными данными. Например, в системе вода (1) – муравьиная кислота (2) при обогащении жидкой фазы водой (см. табл. 2) увеличивается и ее содержание в паровой фазе. Следует отметить, что диапазоны условий, в которых действуют законы Коновалова, ограничены. Первый и третий законы не выполняются в критической точке. Область действия второго закона Коновалова ограничена координатой вблизи критической точки: в изотермических условиях точкой, для которой наблюдается нулевой объемный эффект; в изобарических условиях – точкой, где равен нулю энтропийный эффект. Из законов Коновалова вытекают два следствия: 1) в двойной жидкой системе пар относительно богаче тем компонентом, прибавление которого понижает температуру кипения; 2) максимум или минимум температуры кипения двойной жидкой системы соответствуют жидкость и пар с одинаковым качественным и количественным составом. Смеси полностью смешивающихся жидкостей разделяются на два класса. Смеси первого класса могут быть разделены на чистые компоненты, они не образуют нераздельно кипящих смесей. Смеси второго класса образуют нераздельно кипящие смеси, которые, несмотря на различные температуры кипения чистых веществ, не могут быть разделены перегонкой на чистые компоненты. [39] Законы Вревского Законы Вревского описывают поведение систем при варьировании внешних параметров (температура, давление) при закрепленном составе жидкой фазы. Для их математической интерпретации получим раскрытую форму условия фазового равновесия в виде: dµ1ж - dµ2ж= dµ1п- dµ2п , (34) d(µ1ж - µ2ж)= d(µ1п- µ2п) (35) С учетом соотношений dgп = -sпdTп + VпdPп + µ1dy1 + µ2dy2 , 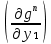 P,T = µ1п-µ2п условие (33) принимает вид: P,T = µ1п-µ2п условие (33) принимает вид:d 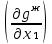 = d = d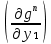 (36) (36)Раскроем полные дифференциалы разности химических потенциалов: d 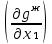 = ( = (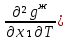 P,x dT + ( P,x dT + (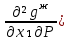 T,x dT + ( T,x dT + (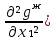 P,T dx1, (37) P,T dx1, (37)d 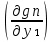 = = 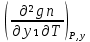 dT + dT + 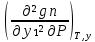 dT + dT +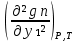 dу1 (38) dу1 (38)Величина второй производной не зависит от порядка дифференцирования (соотношения Максвелла). Тогда, если представить сомножители при переменных уравнений (36) в виде частных производных потенциала: 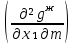 Р,х = Р,х = 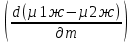 Т,х = Т,х = 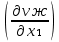 Р,Т =(v1-ж- v2-ж) (39) Р,Т =(v1-ж- v2-ж) (39)где m - число молей. Получим: d 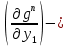 d d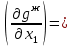 - [(s1-п - s1-ж) - (s2-п - s2-ж)]dT + [(v1-п - v1-ж) - (v2-п - v2-ж)]dP + - [(s1-п - s1-ж) - (s2-п - s2-ж)]dT + [(v1-п - v1-ж) - (v2-п - v2-ж)]dP + 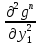 dy1 - dy1 - 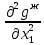 dx1 = 0 (40) dx1 = 0 (40)где верхней планкой обозначены парциальные величины. Последние были введены Льюисом для учета нелинейности зависимостей свойств бинарных смесей от состава. В окончательном виде раскрытая форма условия фазового равновесия выражается следующим образом: 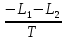 dT + (V1-V2)dP + dT + (V1-V2)dP + 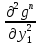 dy1 - dy1 - 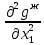 dх1 = 0 (41) dх1 = 0 (41)Здесь Li = 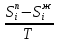 , Vi = Viп - Viж. , Vi = Viп - Viж.При допущении об идеальном поведении паровой фазы и в условиях, удаленных от критических, объемная составляющая в уравнении (41) обращается в нуль. Математический вывод законов Вревского базируется на анализе знаков всех величин, входящих в выражение (41).Их действие ограничено критическими точками фазового равновесия жидкость – пар. [15] Первый закон Вревского. Закон определяет характер влияния внешних параметров на содержание компонента в паровой фазе при закрепленном составе жидкой фазы. С учетом dx1 = 0, выразим из (41) производную состава паровой фазы по температуре: Для идеального пара (V10п = V20п) в условиях, когда объемом жидкой фазы по сравнению с паровой можно пренебречь, знак производной dy1/dT определяется знаком разности парциальных молярных теплот испарения: dy1/dT > 0( < 0), если L1 > L2 (L1 < L2). При постоянном составе жидкой фазы и увеличении температуры пар всегда обогащается тем компонентом, парциальная молярная теплота парообразования которого больше. Парциальные молярные теплоты испарения определяются через теплоты испарения чистых веществ Li0и парциальные избыточные энтальпии компонентов hi-E: Li = Li0 - hi-E (43) При отсутствии экспериментальных данных о теплотах смешения (избыточных энтальпиях) растворов парциальные молярные теплоты испарения Li заменяют теплотами испарения чистых веществLio. Однако для зависимостей L(x), имеющих экстремальные значения, замена величин Рисунок 3 иллюстрирует графическое определение парциальных величин. Значения интегральных теплот испарения совпадают с аддитивными значениями L = L10x1 + L20x2 только в случае атермических растворов, где ΔhE(x) = 0 (рис. 3в) [44]. 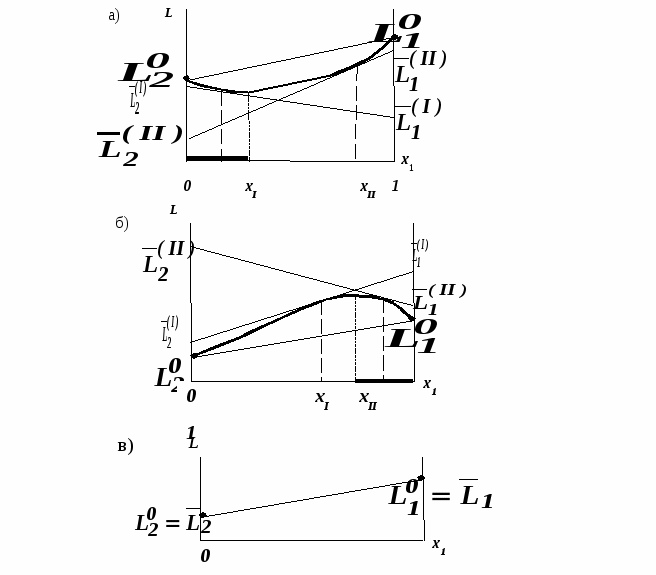 Рис. 3. Примеры определения парциальных молярных теплот испарения компонентов бинарных смесей: а) гетерогенных с; б) гомогенных с; в) атермических. Второй закон Вревского. 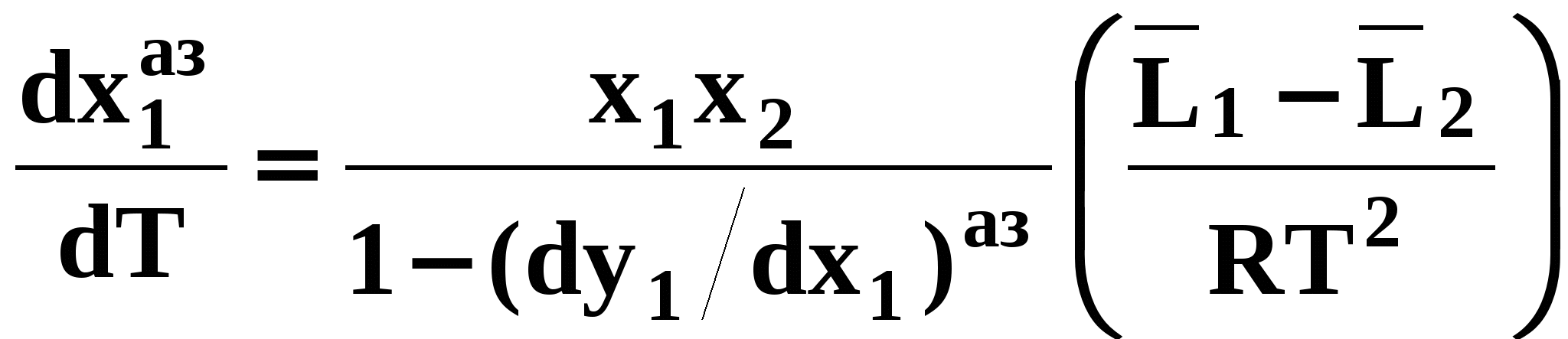 (45) (45)Знак производной dx1аз/dT в уравнении (45) определяется знаком разности парциальных молярных теплот испарения Формулировки второго закона Вревского для азеотропов разных типов: при увеличении температуры (давления): положительный азеотроп обогащается компонентом с большей парциальной молярной теплотой испарения: dx1аз/dT > 0, если dx1аз/dT < 0, если отрицательный азеотроп обогащается компонентом с меньшей парциальной молярной теплотой испарения: dx1аз/dT > 0, если dx1аз/dT < 0, если Анализ экспериментальных азеотропных данных показывает, что в ряде случаев при определении характера обогащения состава азеотропа конкретным компонентом («направление движения» азеотропа) можно ориентироваться на теплоты испарения чистых веществ. Например, для азеотропов бензолциклогексан, циклогексанэтанол и пропанолвода замена не допустима (табл. 3) [25]. Таблица 3. Расчет парциальных молярных теплот испарения бинарных смесей
Эволюция бинарного азеотропа (представлена на рис. 4.), характеризуется соотношениями dx1аз/dT<0. 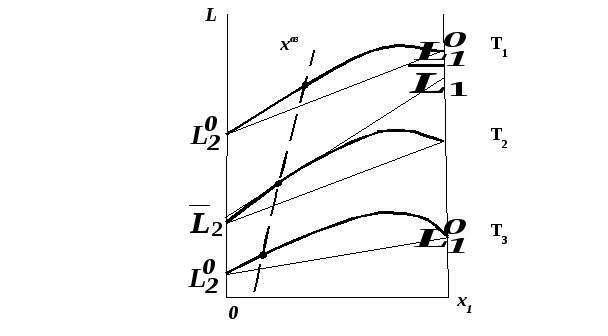 Рис. 4. Эволюция бинарного азеотропа и молярных теплот испарения бинарной системы. Примеры графической иллюстрации второго закона Вревского для разных условий (T1 < T2, P1 < P2) приведены на рис. 5. 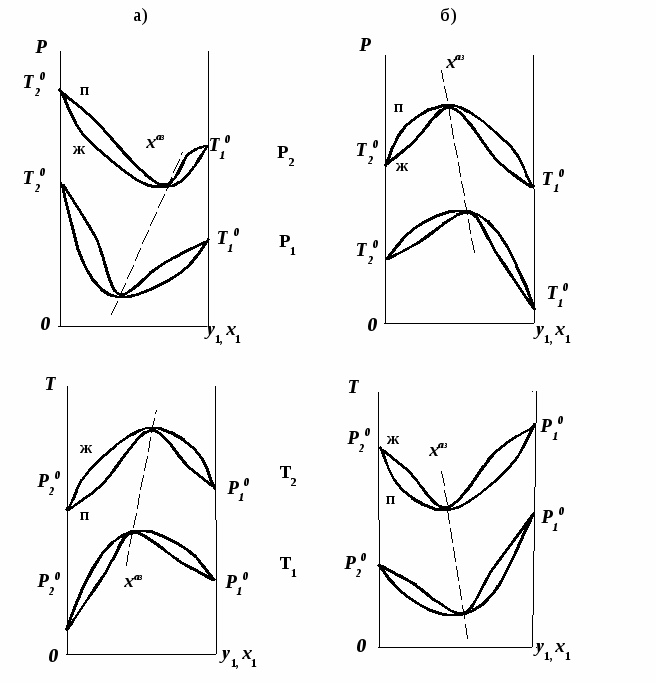 Рис. 5. Примеры иллюстрации второго закона Вревского: При P=const: а) для положительного азеотропа; б) для отрицательного азеотропа; при Т= const: в) для положительного азеотропа; г) для отрицательного азеотропа. Третий закон Вревского. Закон охватывает условия второго и первого законов, которые совместимы в бесконечно малый промежуток времени. Первоначально рассматривают точку азеотропа при определенных температуре и давлении (x1 = x1аз = у1аз), далее, закрепив этот состав (х1аз = const), исследуют изменение состава пара и азеотропа при варьировании температуры (давления). Следовательно, в начальный момент можно приравнять выражения в скобках, полученные из уравнений (42) и (45). В результате имеем результате имеем связь двух производных, отражающих эволюцию составов паровой фазы (dy1/dT)xи азеотропа (dx1аз/dT): 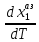 = = 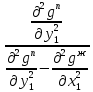 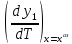 (46) (46)Для точки азеотропа из третьего закона Коновалова (33) выразим отношение вторых производных gпотенциала: 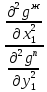 = = 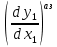 (47) (47)С учетом (45) уравнение (44) имеет вид: 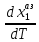 = = 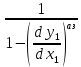 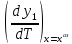 (48) (48)Математический вывод третьего закона Вревского базируется на анализе знаков величин, входящих в уравнение (48). Для положительного азеотропа [1 - (dy1/dx1)аз] > 0 и, следовательно, и dy1/dT имеют одинаковые знаки. Для отрицательного азеотропа [1 - (dy1/dx1)аз] < 0 и производные dx1аз/dT и dy1/dT имеют разные знаки [18]. Формулировка третьего закона Вревского: при увеличении температуры (давления) и для закрепленного состава жидкой фазы для положительного азеотропа изменение составов пара и азеотропа происходит однонаправленно; для отрицательного азеотропа изменение составов пара и азеотропа происходит разнонаправленно. 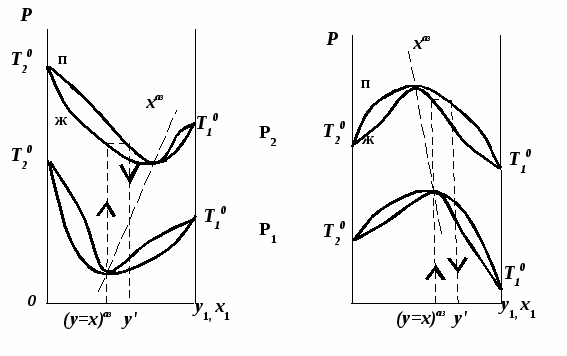 Рис. 6. Графическая интерпретация третьего закона Вревского в системах с азеотропами разных типов: а) положительным; б) отрицательным. Р1 < P2. В системе с положительным азеотропом (рис. 6а) при увеличении температуры (давления) состав азеотропа обогащается компонентом 1. Для закрепленного состава жидкой фазы в паровой фазе также увеличивается содержание этого компонента (y' > yаз). В системе с отрицательным азеотропом (рис. 6 б) имеем иную картину: при увеличении температуры (давления) пар обогащается компонентом 2, а азеотроп компонентом 1 (разнонаправленное изменение). [27] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
