ВКР Сотина. Исследование фазовых эффектов и методов разделения азеотропных смесей, утверждена приказом ргу имени С. А. Есенина от 20 г

• Название: Исследование фазовых эффектов и методов разделения азеотропных смесей, утверждена приказом ргу имени С. А. Есенина от 20 г
• Дата: 30.05.2022
• Размер: 1.21 Mb.
• Имя файла: ВКР Сотина.docx
• Тип: Исследование; #557448
• страница: 5 из 16

1.3. Диаграммы фазового равновесия азеотропных систем

Состояние двухфазной бинарной системы жидкость  пар определяется двумя независимыми переменными. Парожидкостное равновесие (ПЖР) обычно изучают при изобарических (при постоянном давлении) или изотермических условиях (постоянной температуре). На рис. 7-9 схематически представлены основные типы диаграмм равновесия жидкость  пар бинарных систем.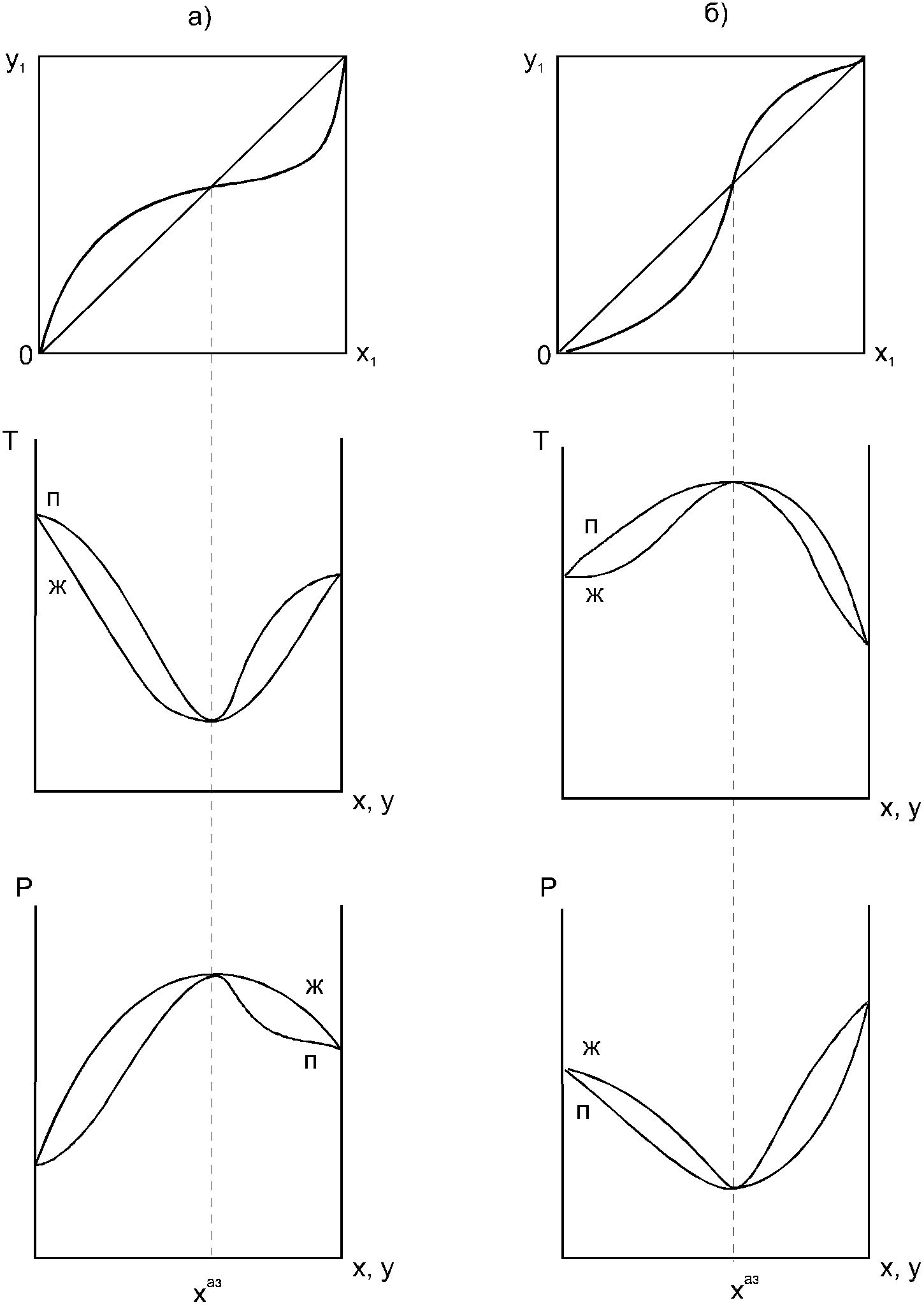



Рис. 7. Диаграммы фазового равновесия жидкостьпар гомогенных азеотропных систем:

а - положительный азеотроп, б - отрицательный азеотроп.

При изучении гомогенных систем (рис. 7) в качестве параметров состояния выбирают температуру, давление и концентрацию одного из компонентов (обычно компонент 1 имеет меньшую температуру кипения). Данные системы являются двухфазными, т. е. состоят из двух фаз: жидкой и паровой.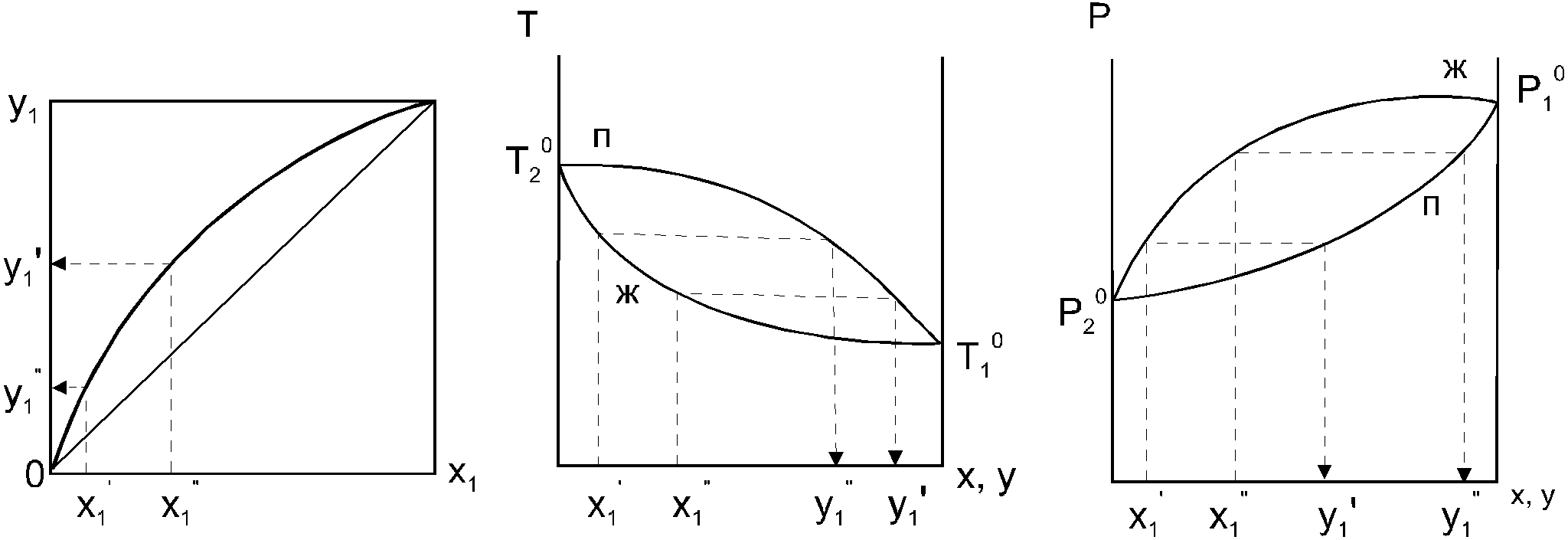



Рис. 8. Диаграммы фазового равновесия жидкостьпар зеотропной гомогенной системы.

При ограниченной взаимной растворимости компонентов бинарная система характеризуется наличием областей с тремя равновесными фазами: две жидкие и одна паровая (рис.8). Такая трехфазная система имеет только одну степень свободы, т. е. состояние системы определяется заданием одного из параметров температуры, давления или состава равновесной фазы.

По характеру отклонения от идеального поведения бинарные смеси подразделяются на системы с положительными, отрицательными и смешанными отклонениями [11].

Идеальные системы описываются законом Рауля:

y_iP = x_iP_i⁰ (49)

Отклонения от идеальности учитываются введением соответствующих коэффициентов: активности (γ_i) для жидкой фазы и летучести (φ_i) для паровой фазы. Поведение паровой фазы обычно принимают идеальным (φ_i = 1), тогда уравнение (49) для реальных систем имеет вид:

y_iP = x_iP_i⁰γ_i (50)

Для положительных отклонений γ_i > 1, lnγ_i > 0, для отрицательных 0 < γ_i < 1, lnγ_i < 0, для смешанных отклонений lnγ_i имеет разные знаки.

Азеотроные системы можно разделить также на зеотропные (рис. 8, 9а) и азеотропные (рис. 7, 9б-г). Гетероазеотропные системы имеют азеотроп в области сосуществования двух равновесных жидких фаз, который реализуется только при положительных отклонениях от идеального поведения.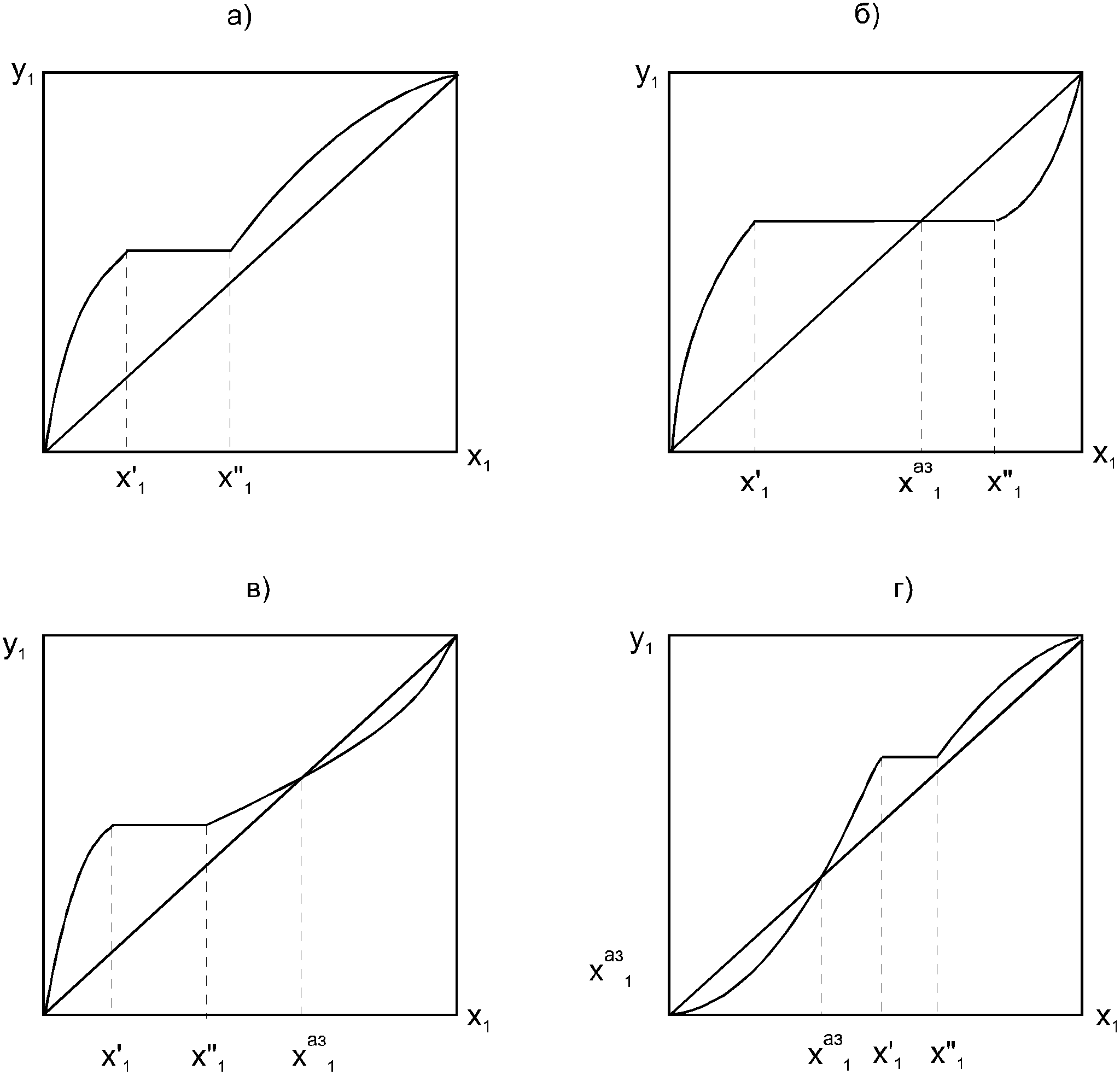



Рис. 9. Диаграммы фазового равновесия бинарных расслаивающихся систем:

а) зеотропная, б) гетероазеотропная, в) с гомогенным азеотропом,

г) со смешанными отклонениями от идеального поведения(расслаивание и отрицательный азеотроп).

Азеотроп характеризуется равенством составов паровой и жидкой фаз и наличием экстремума по температуре (в изобарических условиях) или давлению (в изотермических условиях), что вытекает, как будет показано далее, из первого закона Коновалова. В точке азеотропа наблюдается равенство единице коэффициента распределения компонентов k_i и коэффициента относительной летучести α_ij:

k_i^аз = y_i/x_i = 1 (51)

α_i^аз = k_i/ k_j = 1 (52)

где k_i,j - коэффициент равномерного распределения компонента i, j между паровой и жидкой фазами.

Соотношения (51)-(52) используют для определения параметров азеотропной точки при интерполяции экспериментальных данных по ПЖР.

Фазовые диаграммы графически отображают состояния равновесной системы в пространстве термодинамических переменных, например: температуры, давления и состава. Число фаз в бинарных системах может быть различно.

Состояние двухфазной бинарной системы жидкость  пар определяется двумя независимыми переменными, в качестве которых обычно выбирают концентрацию одного компонента и внешний параметр (температуру Т или давление Р). Примеры даны на рис. 10.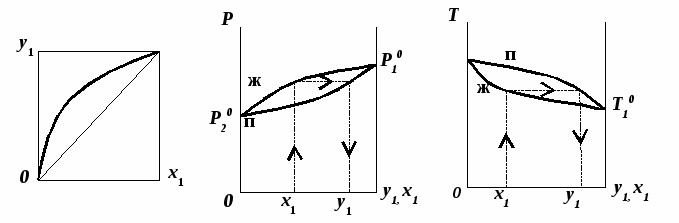



Рис. 10. Диаграммы фазового равновесия жидкость - пар бинарных зеотропных систем: а) у - х, б)Р - х - у; в)Т - х - у.

Фазовые равновесия жидкость – жидкость и жидкость – твердое тело экспериментально исследуют при постоянном давлении, в качестве независимых переменных выступают состав и температура (рис. 11). Состояние трехфазной бинарной системы жидкость  жидкость – пар в области расслаивания определяется одной независимой переменнойf=1 (Т,Р или состав).

На рис. 11 представлены наиболее распространенные примеры фазовых диаграмм жидкость – твердая фаза и жидкость – жидкость – пар. Их полные множества включают большее число типов.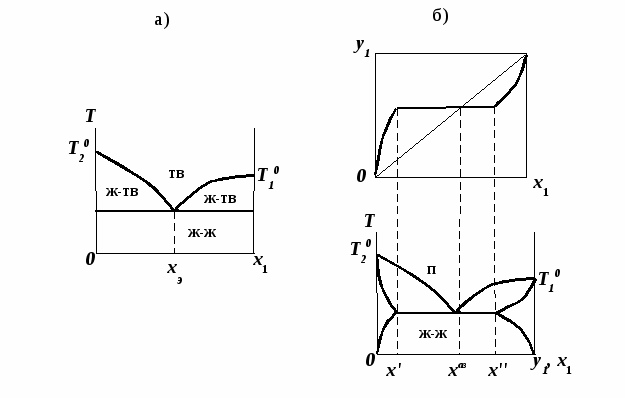



Рис. 11. Примеры фазовых диаграмм бинарных систем с ограниченной взаимной растворимостью компонентов в изобарических условиях:

а) жидкость - твердая фаза; б) жидкость - жидкость - пар.

На рис. 12 приведены более сложные диаграммы бинарных расслаивающихся систем.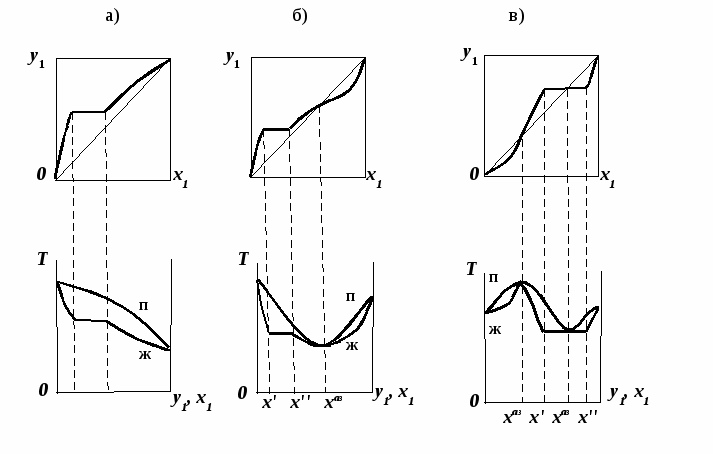



Рис. 12. Примеры фазовых диаграмм жидкость - жидкость - пар бинарных систем в изобарических условиях: а) зеотропная система;

б) расслаивание жидкой фазы и гомогенный азеотроп;

в) отрицательный азеотроп и гетерогенный азеотроп.

Здесь x', x'' – составы равновесных жидких фаз.

Диапазоны условий, в которых изучают фазовые равновесия, ограничены критическими точками [11]. Это предельные точки на кривых равновесия фаз, в окрестностях которых фазовое равновесие нарушается, происходит потеря термодинамической устойчивости и фазы становятся неразличимыми.

Условие устойчивости фазы приведено ниже: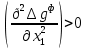

(53)

Критическая точка фазового равновесии жидкость – пар является конечной точкой на кривой испарения и характеризуется критическими значениями температуры Т_с, давления Р_с и объема V_c. Фазовый переход твердая фаза – жидкость характеризуется критической температурой плавления. Парожидкостное равновесие существует в диапазоне условий (Р, Т), ограниченном этими критическими точками.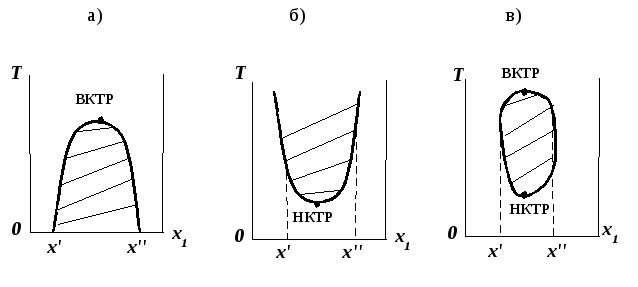



Рис. 13. Критические точки растворимости бинарных систем (Р=const):

а) верхняя критическая точка растворимости;

б) нижняя критическая точка растворимости;

в) две критические точки растворимости.

На рис. 13 приведены диаграммы фазового равновесия жидкость – жидкость. Линии, соединяющие составы равновесных фаз (x' ,x''), называются нодами жидкость-жидкость. Бинодаль – линия составов равновесных жидких фаз, отделяющая расслаивающуюся часть диаграммы от гомогенной (рис. 13).[45]

В большинстве бинарных систем взаимная растворимость компонентов увеличивается при повышении температуры (рис. 13а). В верхней критической точке растворимости (ВКТР) жидкие фазы становятся неразличимыми, при дальнейшем повышении Т смесь является гомогенной.

В системах с нижней критической точкой растворимости (НКТР) увеличение температуры приводит к уменьшению взаимной растворимости (рис. 13б). Смеси с двумя критическими точками растворимости встречаются значительно реже (рис. 13в).

Данные фазовых равновесий жидкость – пар (гомогенная жидкая фаза) и жидкость – жидкость – пар (ограниченная взаимная растворимость компонентов) используются для расчетов ректификации бинарных смесей.

Диаграммы жидкость – жидкость необходимы при разработке экстракционного разделения и комплексов, сочетающих ректификацию и расслаивание жидкой фазы. Диаграммы жидкость – твердая фаза необходимы при разработке комплексов разделения бинарных смесей, сочетающих ректификацию и кристаллизацию [20].