Курсовая. Курсовая работа Гнездилов Р.Г ИТ-81з. Исследование систем массового обслуживания с ожиданием
 Скачать 1.32 Mb. Скачать 1.32 Mb.
|
1.2 Простейший потокПоток заявок называется простейшим, если вероятность поступления в систему ровно k заявок, k=0, 1, 2, …, в течение времени t определяется по формуле 1: 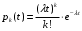 (1) (1)где λ > 0 – постоянное число, называемое интенсивностью потока [5]. 1.3 Описание функционирования марковского процесса с непрерывным временемДопустим, в любой момент времени система будет находиться в одном из состояний S1, S2, …, Sm. Пусть X(t) – случайный процесс, равный номеру состояния, в котором находиться система в момент времени t. Рассматривая изменение состояния системы, будем считать, что процесс перешел из одного состояния в другое. При этом время на такой переход не тратится. Случайный процесс X(t) называется марковским, если будущее процесса зависит только от его настоящего и не зависит от прошлого. Такое свойство называется отсутствием последействия. Предыстория процесса влияет на его дальнейшее развитие, но все это влияние сосредоточено в настоящем. Выделение марковских процессов может быть обусловлено рядом причин, важнейшими из которых являются относительная простота случайного процесса, описывающего эволюцию системы, наличие возможности использовать хорошо разработанный математический аппарат для аналитического исследования марковских процессов, возможность получения аналитических выражений для показателей качества систем, и, наконец, возможность сведения к указанным моделям более общих моделей. Однородный марковский процесс X(t) с дискретным множеством состояний S1, S2, …, Sm и непрерывным временем определяется постоянными интенсивностями перехода (формула 2). 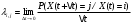 (2) (2)из состояния Si в состояние Sj, а также начальным вектором распределения вероятностей: pi(0)=P(X(0)=i), i=1,2,…, m. Пусть pi(t) вероятность пребывания системы в момент времени t в состоянии Si, i = 1, 2, ..., m. Эти вероятности удовлетворяют системе обыкновенных дифференциальных уравнений А.Н. Колмогорова (3): 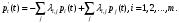 (3) (3)которая составляется по следующему правилу: для каждого состояния Si записывается уравнение, в левой части которого стоит производная от pi(t), а в правой части – сумма произведений вероятностей всех состояний, умноженных на интенсивности перехода из этих состояний в состояние Si. Причем произведения, соответствующие выходам из состояния Si, берутся со знаком «-», а произведения, соответствующие входам в состояние Si, берутся со знаком «+». Из системы уравнений Колмогорова можно получить модель функционирования системы при длительной ее эксплуатации, то есть при 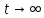 . В этом случае pi(t) . В этом случае pi(t) 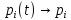 и и 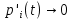 . Вероятности pi называются стационарными или финальными вероятностями. Относительно этих вероятностей имеет место система линейных алгебраических уравнений (4): . Вероятности pi называются стационарными или финальными вероятностями. Относительно этих вероятностей имеет место система линейных алгебраических уравнений (4):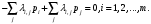 (4) (4)Пример. На рисунке 2 представлен граф состояний системы, дугам которого приписаны постоянные интенсивности перехода из состояния в состояние. В момент времени t = 0 система находилась в состоянии S1. Необходимо составить математическую модель для нестационарного и стационарного режима функционирования системы. 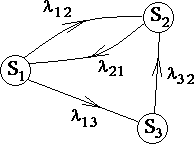 Рисунок 2 – Граф состояний системы Приведенное выше правило позволяет записать следующую систему дифференциальных уравнений (5): 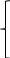 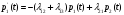 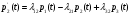 (5) (5)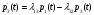 Так как при t = 0 система находилась в состоянии S1 , то имеют место начальные условия: p1(0) = 1, p2(0) = 0, p3(0)=0. Решение системы при заданных начальных условиях (аналитическими или численными методами) помогает найти вероятности пребывания системы pi(t) в каждом состоянии, i = 1,2,3. Из системы дифференциальных уравнений мы получаем математическую модель функционирования системы при длительной эксплуатации: 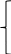 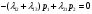 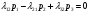 (6) (6)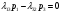 Данная система является неопределенной и должна решаться при дополнительном условии: p1 + p2 + p3 = 1. Из решения системы алгебраических уравнений определяются финальные вероятности pi, i = 1,2,3. |
