Курсовая. Курсовая работа Гнездилов Р.Г ИТ-81з. Исследование систем массового обслуживания с ожиданием
 Скачать 1.32 Mb. Скачать 1.32 Mb.
|
1 Краткие теоретические сведения1.1 Основные понятияСистемой массового обслуживания (СМО) называется совокупность потока заявок (требований), поступающих в систему, и приборов (каналов), обслуживающих эти заявки. Поток заявок обычно носит случайный характер. Теория массового обслуживания занимается разработкой и анализом математических моделей, описывающих системы массового обслуживания. Образцы концепций общественного сервиса: механические телефонные станции также прибывающие в их призывы, торговые центры также потребители, компании домашнего сервиса также покупатели, исправительные студийные также оборудование, вызывающая ремонтных работ, электронно-вычислительная машина также проблемы, прибывающие в разрешение, аэропорты также летательные аппараты, вызывающие высадки, педагоги также изнемогающие экзамены учащиеся, также полиадельфит. буква. Главной составляющей концепций общественного сервиса считается формирование очередности в сервис, по этой причине концепцию общественного сервиса установлено именовать кроме того точной концепцией очередностей. Следует подразумевать, то что во концепции общественного сервиса разговор проходит об исследованию точных модификаций, имеющих необходимой ступенью абстракции. Тут никак не значима сущность обслуживаемых заказов также их физиологические качества. Значительно значимыми считаются только факторы возникновения данных заказов, таким образом равно как с их находится в зависимости развитие модификации в периода. Во теоретической модификации отсутствует потребности анализировать физиологическую сторонку хода сервиса. Обстирать заявку - данное означает употребить в ее определенное период во согласовании со установленной выдержкой сервиса [1]. Любая концепция общественного сервиса способен являться изображена, как показано на рисунке 1. 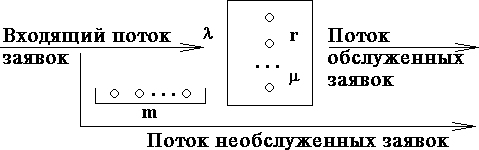 Рисунок 1 – Схематическое изображение системы массового обслуживания Объясним один из возможных вариантов функционирования системы. Допустим, на обслуживание поступает поток заявок, который характеризуется параметром λ. В системе имеется r обслуживающих каналов (приборов). Если в системе есть свободные каналы, то вновь пришедшая заявка поступает на свободный канал и начинается ее обслуживание. Время обслуживания случайное и характеризуется параметром µ. По окончании обслуживания образуется поток обслуженных заявок. Если все каналы заняты обслуживанием, то вновь пришедшая заявка становится в очередь (поступает в бункер или накопитель) емкостью m. Это означает, что в очереди может находиться не более, чем m заявок. Если количество заявок в очереди превысит m, то такие заявки покидают систему не обслуженными, образуя поток необслуженных заявок. Работа системы массового обслуживания сопровождается рядом случайных факторов. Поток поступающих заявок представляет случайный процесс – число заявок является случайной функцией времени. Время, которое требуется для обслуживания одной заявки (время обслуживания) является случайной величиной [2]. Основные понятия систем массового обслуживания: входящий поток заявок и его интенсивность, очередь на обслуживание, число обслуживающих каналов (приборов), время обслуживания заявки, дисциплина и приоритет обслуживания заявки (порядок выбора заявок из очереди), потоки обслуженных и необслуженных заявок. Системы массового обслуживания систематизируются во связи с типа струи заказов также нрава их сервиса. Отличают концепции со утратами (со отказами) также со очередностью (со ожиданием). В Случае Если обращение действует во концепцию со утратами во в таком случае период, если все без исключения каналы захвачены (m=0), в таком случае возлюбленная приобретает «отказ» также пропадает. Образцом такого рода концепции считается телефонная база. Во концепциях со очередностью обращение, приползшая во период, если каналы захвачены, возникает во очередность также ждет, до тех пор пока никак не станет свободной единственный с каналов. Имеются концепции со безграничной очередностью, если количество зон во очередности никак не лимитировано (m=∞) также концепции со узкой очередностью. Лимитирования случаются различные - согласно количеству заказов, в то же время важных во очередности, согласно периода присутствия заказы во очередности, согласно периода деятельность концепции также полиадельфит. буква. По числу обслуживающих каналов различают одноканальные (r=1) и многоканальные (r>1) системы массового обслуживания. Для многоканальной системы будем считать, что каждая заявка обслуживается любым из каналов. Такая система каналов называется полнодоступным пучком [3]. В системах с очередью учитывается также дисциплина обслуживания. Часто заявки обслуживаются в порядке их поступления в систему по принципу «первый пришел – первый обслужен» (прямой приоритет). Но возможны и другие правила обслуживания заявок: «последний пришел – первый обслужен» (обратный приоритет), или «первой обслуживается заявка с заданным номером» (назначенный приоритет), или «первой обслуживается заявка со случайным номером» (случайный приоритет). Также, вполне возможно обслуживание заявки вне очереди. При этом заявка с более высоким приоритетом, поступив в систему, может оборвать уже начавшееся обслуживание заявки с меньшим приоритетом, а может дождаться окончания ее обслуживания. В первом случае говорят об абсолютном, а во втором – об относительном приоритете. Основоположником теории массового обслуживания является датский математик А.К. Эрланга, который в 1909 г. опубликовал важные результаты, полученные им при изучении математических моделей телефонных систем. В настоящее время модели и методы массового обслуживания находят приложения во многих областях науки и техники, начиная с контроля над приземлением самолетов и кончая теорией управления запасами, от исследований, связанных с ростом бактерий, – до составления больничных графиков [4]. |
