Курсовая. Курсовая работа Гнездилов Р.Г ИТ-81з. Исследование систем массового обслуживания с ожиданием

• Название: Исследование систем массового обслуживания с ожиданием
• Анкор: Курсовая
• Дата: 12.05.2022
• Размер: 1.32 Mb.
• Имя файла: Курсовая работа Гнездилов Р.Г ИТ-81з.docx
• Тип: Курсовой проект; #525817
• страница: 7 из 8

2.2 Математическая модель стационарного режима

Пусть p_k – стационарная вероятность пребывания системы в состоянии S_k, k = 0,1,2,3,4. Тогда имеет место следующая система алгебраических уравнений, описывающая стационарный режим 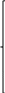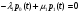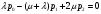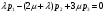(19):








(19)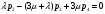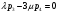




Эту систему следует решать вместе с условием нормировки 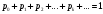(20):
(20)
Воспользуемся для этой цели электронной таблицей Excel. На Листе 1, как показано на рисунке 5, в ячейки A2 и B2 поместим значения интенсивностей λ и µ. Блок ячеек E6:I6 зарезервируем для записи значений искомых вероятностей p₀, p₁, p₂, p₃, p₄ (отмечены желтым цветом). Эти ячейки сначала пустые. В блоке ячеек E7:I7 поместим коэффициенты при неизвестных системы (19), за исключением последнего уравнения. Последнее уравнение системы (19) заменим условием нормировки (20), тогда в блоке ячеек E11:I11 будут располагаться «единицы».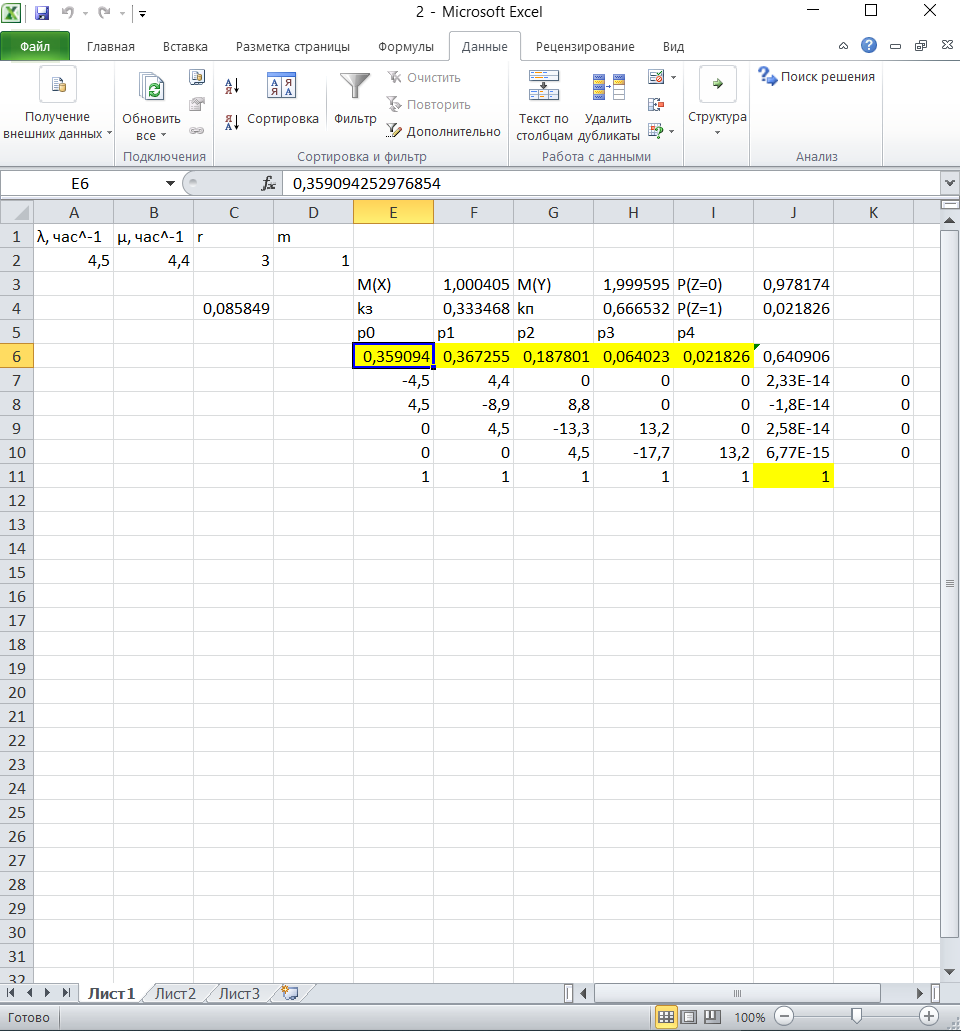


Рисунок 5 – Пример листа Excel
Блок ячеек J7:J11 содержит формулы для записи левых частей системы уравнений (17) и (18), а именно, в клетку I4 поместим формулу =СУММПРОИЗВ($E$6:$I$6;E7:I7), которую протянем на блок ячеек J7:J10. В блоке ячеек K7:K10 содержатся правые части системы (19), равные «нулям».

Обращение к процедуре «Поиск решения» позволит нам найти решение системы уравнений (19). Для этого нужно в появившемся окне указать:

- целевую ячейку, в данном случае I8, равную значению 1 (условие нормировки);

- изменяемые ячейки, в данном случае блок E6 : I6;

- ограничение, в данном случае J7 : J10 = K7 : K10.

После нажатия клавиши «Выполнить» в блоке E6 : I6 получаем решение системы уравнений. Таким образом, стационарные вероятности равны: p₀=0.359094, p₁=0.367255, p₂=0.187801, p₃=0.064023, p₄=0.021826.

2.3 Стационарные характеристики СМО

На основе данных значений вероятностей пребывания системы в состояниях определяются требуемые показатели эффективности стационарного режима. А именно:

- p₀=0.359094 вероятность того, что все машины свободны.

- p₁=0.367255 вероятность того, что одна машина занята работой.

- p₂=0.187801 вероятность того, что две машины заняты работой.

- p₃=0.064023 вероятность того, что три машины заняты работой.

- p₄=0.021826 вероятность того, что три машины заняты работой и одно бревно в очереди.

Теперь рассмотрим другие показатели эффективности работы системы массового обслуживания.

Пусть X – число машин, занятых обслуживанием бревен. Это есть случайная величина с возможными значениями: 0, 1, 2, 3. Вероятности этих значений соответственно равны:
P(X=0) = p₀ = 0.359094

P(X=1) = p₁ = 0.367255

P(X=2) = p₂ = 0.187801

P(X=3) = p₃+p₄ = 0.085849
Тогда среднее число машин, занятых обслуживанием бревен, есть математическое ожидание случайной величины X , которое равно:
M(X)=0‧P(X=0)+1‧P(X=1)+2‧P(X=2)+3‧P(X=3)=1.0004
Следовательно, среднее число работающих машин равно 1.

Пусть Y – число свободных машин. Это есть случайная величина с возможными значениями: 0, 1, 2, 3. Вероятности этих значений соответственно равны:
P(Y=0)= p₃+p₄=0.085849

P(Y=1)= p₂=0.187801

P(Y=2) = p₁=0.367255

P(Y=3) = p₀=0.359094
Тогда среднее число свободных машин есть математическое ожидание случайной величины Y , которое равно:
M(Y)=0‧P(Y=0)+1‧P(Y=1)+2‧P(Y=2)+3‧P(Y=3)=1.9996
Следовательно, среднее число простаивающих машин равно 2. Общее число работающих и свободных машин равно:
M(X)+M(Y)=r=3
Коэффициент загрузки машин равен отношению среднего числа работающих машин к общему числу машин в системе обслуживания, т.е. в процентах он примет следующий вид: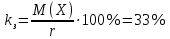

Коэффициент простоя машин равен отношению среднего числа свободных машин к общему числу машин в системе обслуживания, т.е. в процентах он примет следующий вид: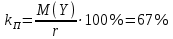

Пусть Z – число бревен в очереди. Это есть случайная величина с возможными значениями: 0, 1. Вероятности этих значений соответственно равны:
P(Z=0)=p₀+p₁+p₂+p₃=0.97817

P(Z=1)=p₄=0.02183
Тогда среднее число бревен в очереди есть математическое ожидание случайной величины Z , которое равно:
M(Z)=0‧P(Z=0)+1‧P(Z=1)= 0.02183
Очевидно, среднее число бревен, находящихся в очереди равно 0.02, т.е. значительно меньше одной штуки.