Курсовая. Курсовая работа Гнездилов Р.Г ИТ-81з. Исследование систем массового обслуживания с ожиданием
 Скачать 1.32 Mb. Скачать 1.32 Mb.
|
2.4 Математическая модель нестационарного режимаОбозначим через pk(t) вероятность пребывания системы в момент времени t в состоянии Sk, k = 0,1,2,3,4 . Это – переходные вероятности, изменяющиеся со временем. Согласно правилу, сформулированному в п.1.3, нестационарный режим описывается следующей системой дифференциальных уравнений, составленной по графу состояний, изображенному на рисунке 4: 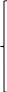 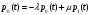 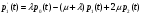 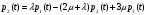 (21) (21)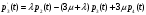 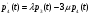 Решение этой системы должно удовлетворять начальному условию: p0(0)=1, p1(0)=p2(0)=p3(0)=p4(0)=0 (22) означающему, что в момент времени t = 0 система находится в состоянии S0: бревен в системе обслуживания нет, машины простаивают и очередь отсутствует. Контролем правильности решения системы является условие нормировки: 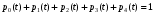 (23) (23)которое означает, что для любого момента времени сумма вероятностей постоянна и равна p0=1 . Это следует из замечания п.1.6. Решение задачи (21)-(22) получим в Excel на Листе 2 методом Эйлера, как показано на рисунке 6. 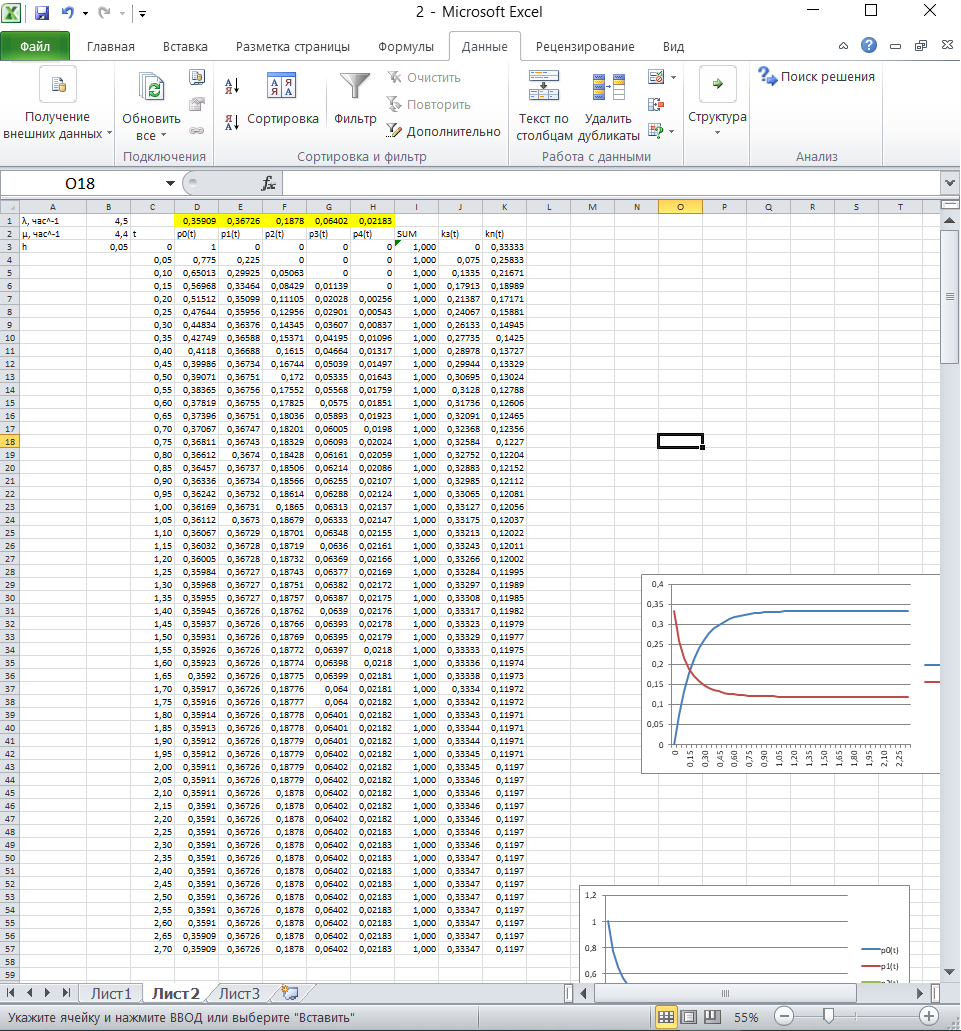 Рисунок 6 – Решение задач методом Эйлера В ячейки B1 и B2 поместим значения интенсивностей λ и µ. В ячейку B3 поместим значение шага интегрирования h. Примем, сначала h = 0,1 . Блок ячеек C3 : H3 зарезервируем для записи времени начала функционирования системы t = 0 и начальных вероятностей p0(0), p1(0), p2(0) p3(0), p4(0). В блоке ячеек C4 : H4 поместим формулы Эйлера из п.1.6, по которым рассчитываются вероятности для текущего момента времени t по известным вероятностям для предыдущего момента времени t - h. Эти формулы приведены в таблице 7. Таблица 7 – Формулы для решения систем дифференциальных уравнений
Протягивая эти формулы вниз, мы получим решение системы уравнений. В рисунке 6 колонка I служит для контроля правильности введенных соотношений, а также для контроля правильности выбора шага интегрирования. В клетку I3 запишем формулу СУММ(D3:H3), которую протянем вниз. Для принятого шага h = 0,1 элементы этой колонки не равны «единице». Уменьшим шаг интегрирования до h = 0,05 . Теперь все элементы колонки I станут равными «единице». Это означает правильность решения системы дифференциальных уравнений (21). Вероятности pk(t) с ростом времени t стремятся к своим стационарным значениям pk, не зависящим от времени и полученным в п.2.2 [10]. Поэтому таблицу вероятностей необходимо вычислять до тех пор, пока ни будут выполняться соотношения: p0≈0.35909, p1≈0.36726, p2≈01878, p3≈0.06402, p4≈0.02183. Как показано в таблице 2, указанные соотношения выполняются с точностью до трех знаков после запятой уже для момента времени t = 1,7. Графическая иллюстрация вероятностей из рисунка 6 показана на рисунке 7. 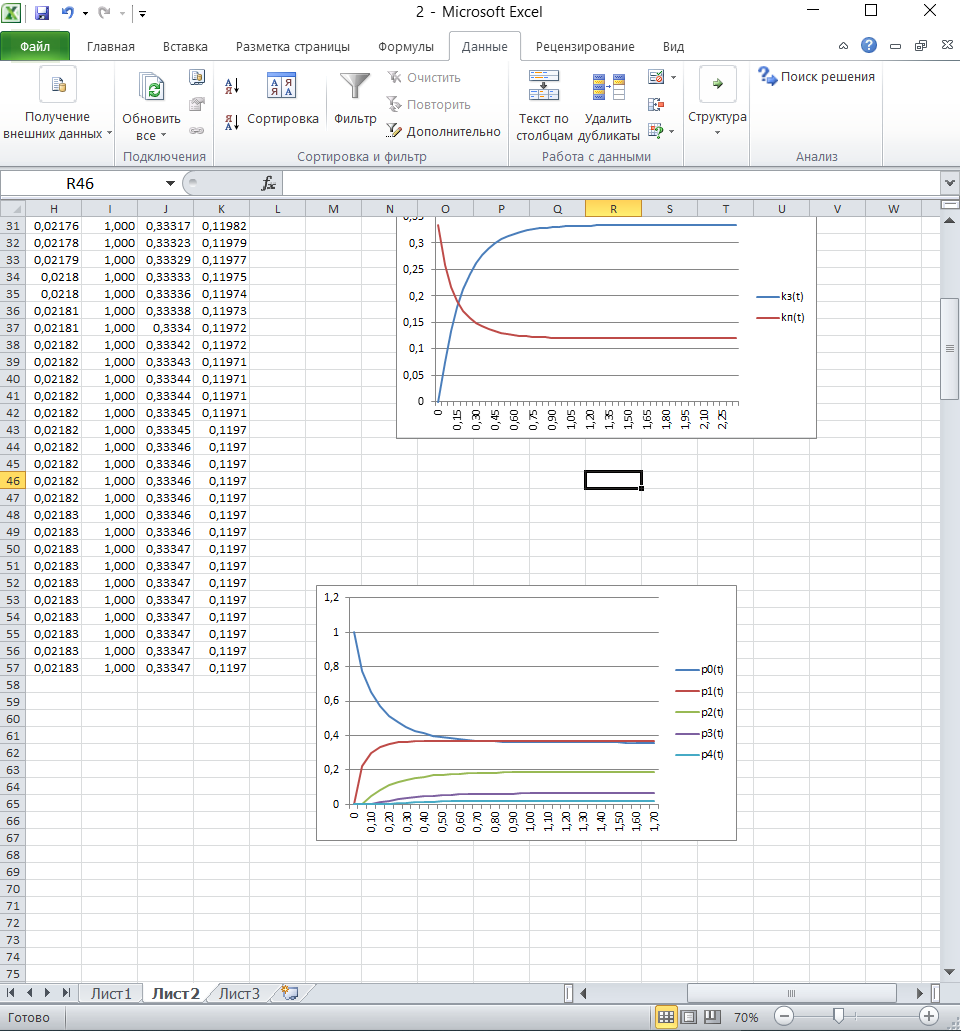 Рисунок 7 – Вероятности состояний системы Рисунок 7 показывает достаточно быстрое вхождении процесса в стационарный режим, при котором вероятности практически не изменяются, а графики становятся параллельными оси времени. 2.5 Нестационарные характеристики СМОРассчитанные вероятности состояний системы, а также соотношения позволяют определить коэффициенты загрузки и простоя системы в зависимости от времени. Для СМО вида M /M / 2/ 1 указанные соотношения принимают вид: 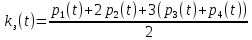 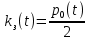 Можно дополнить таблицу 6 колонками J и K, в которые поместим соотношения для вычисления коэффициентов загрузки и простоя, которые протянем вниз. В итоге получим таблицу, показанную на рисунке 8. 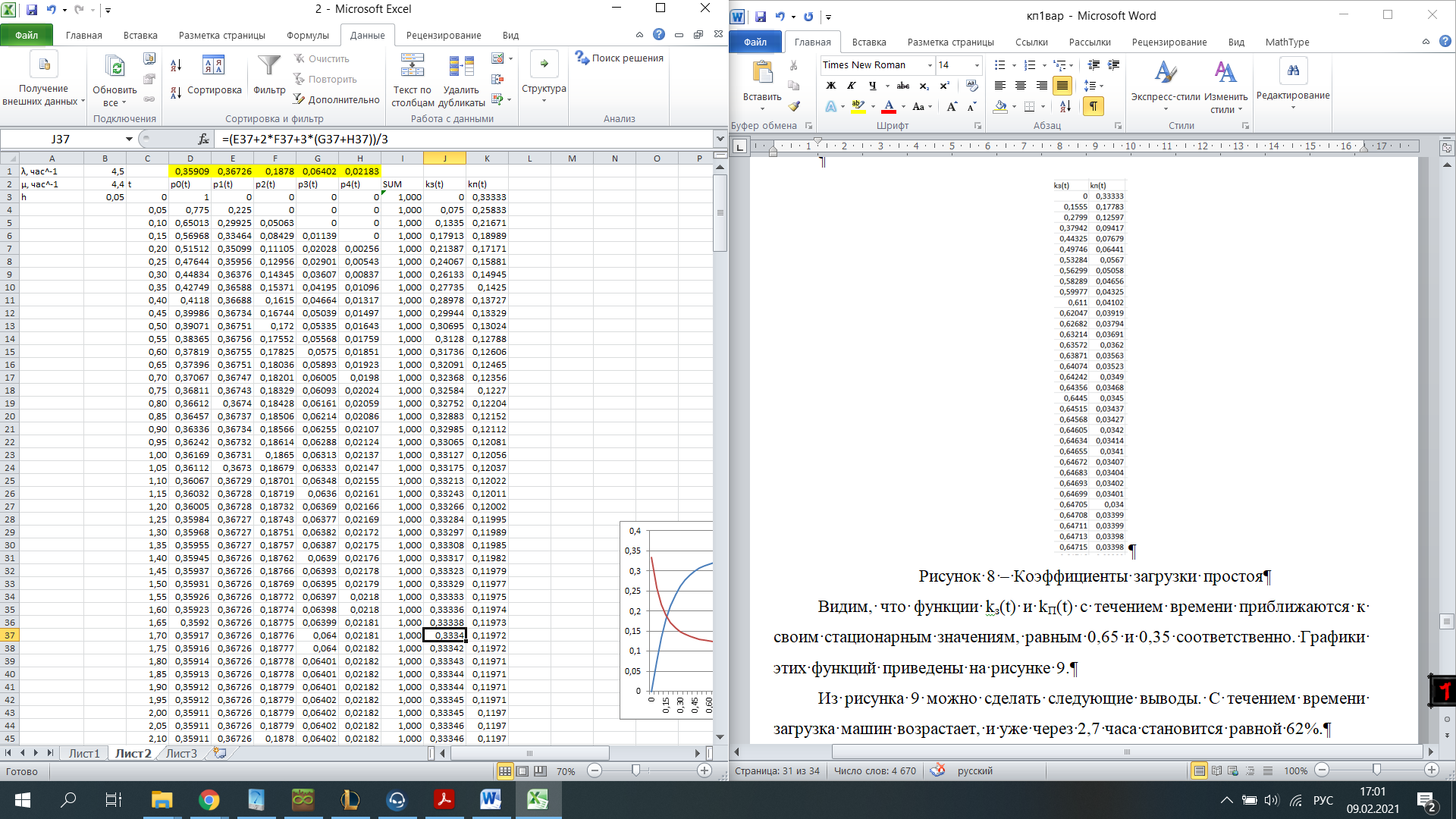 Рисунок 8 – Коэффициенты загрузки простоя Мы видим, что функции kз(t) и kП(t) с течением времени приближаются к своим стационарным значениям, равным 0,33 и 0,67 соответственно. Графики этих функций приведены на рисунке 9. Из рисунка 9 можно сделать следующие выводы. С течением времени загрузка машин возрастает, и уже через 1,7 часа становится равной 33%. 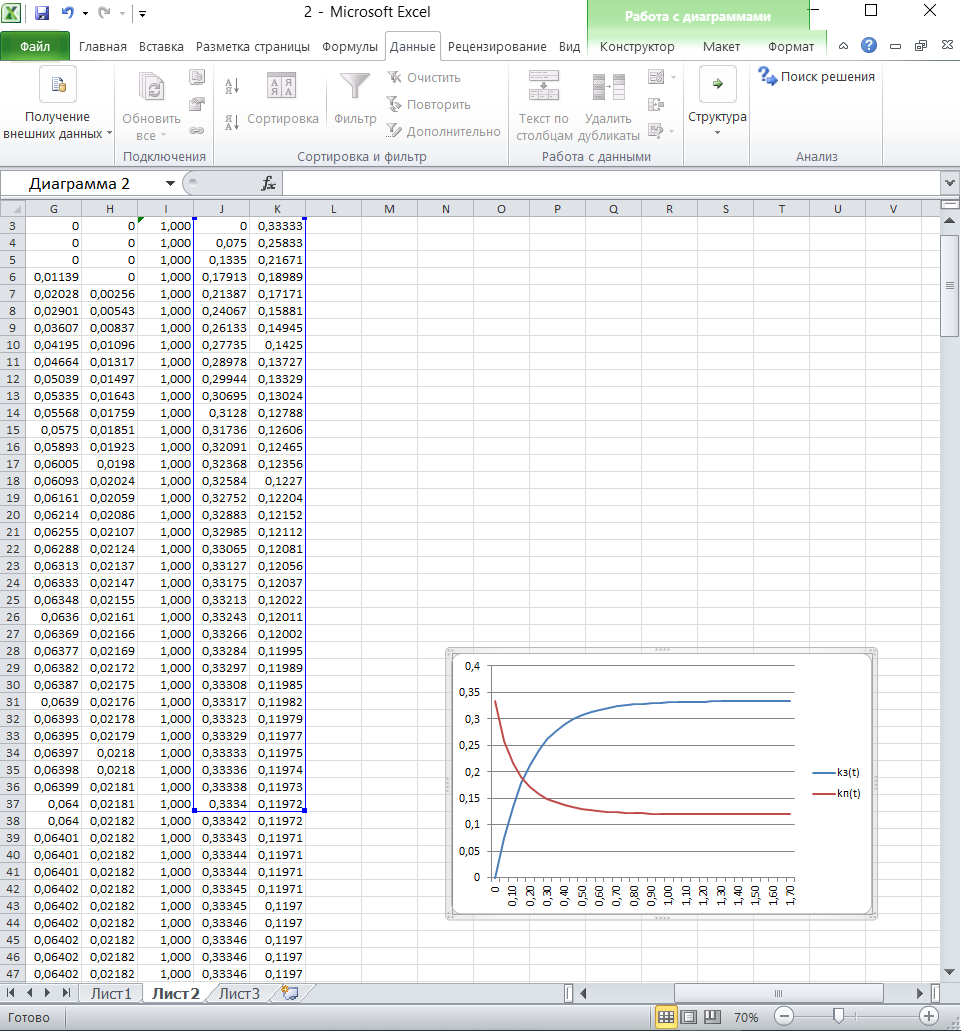 Рисунок 9 – Коэффициенты загрузки и простоя машин в цехе Коэффициент простоя машин с течением времени убывает и примерно через час составляет 67%. Это означает, что машины загружены очень слабо и вполне возможно осуществление в системе обслуживания таких мероприятий, как: - увеличение потока бревен, - уменьшение количества машин для распила, - уменьшение длины очереди, - установка менее производительных и более дешевых машин. Но стоит учитывать, что замена машин приведет к увеличению времени обслуживания, поэтому при возможном значительном повышении нагрузки лучше прибегнуть к первым трем мероприятиям. Такие действия целесообразны только при стабильном потоке бревен, который рассматривался в работе, либо же при незначительном увеличении интенсивности потока, а также различной степени уменьшения количества поступающего сырья для обработки. 3 ЗадачаПользуясь моделью СМО M / M / v / K для подсистемы ТфОП, определить среднюю задержку запроса на информационные услуги в очередях контакт-центра. Определить число операторов, обеспечивающее среднюю задержку запроса на информационные услуги не более 30 сек. Число K определяется как сумма числа операторов ТфОП и числа мест для ожидания. Таким образом K=15+5=20. Рассчитаем коэффициент загрузки системы, для этого интенсивность поступления заявок разделим на интенсивность обслуживания: 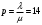 Вероятность того, что в системе не будет вызова, определяется по формуле: 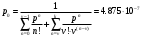 Известно, что все вызовы, поступающие на систему, когда она находится в состоянии n=k , теряются. Таким образом, можно вычислить вероятность нахождения системы в состоянии n по следующей формуле: 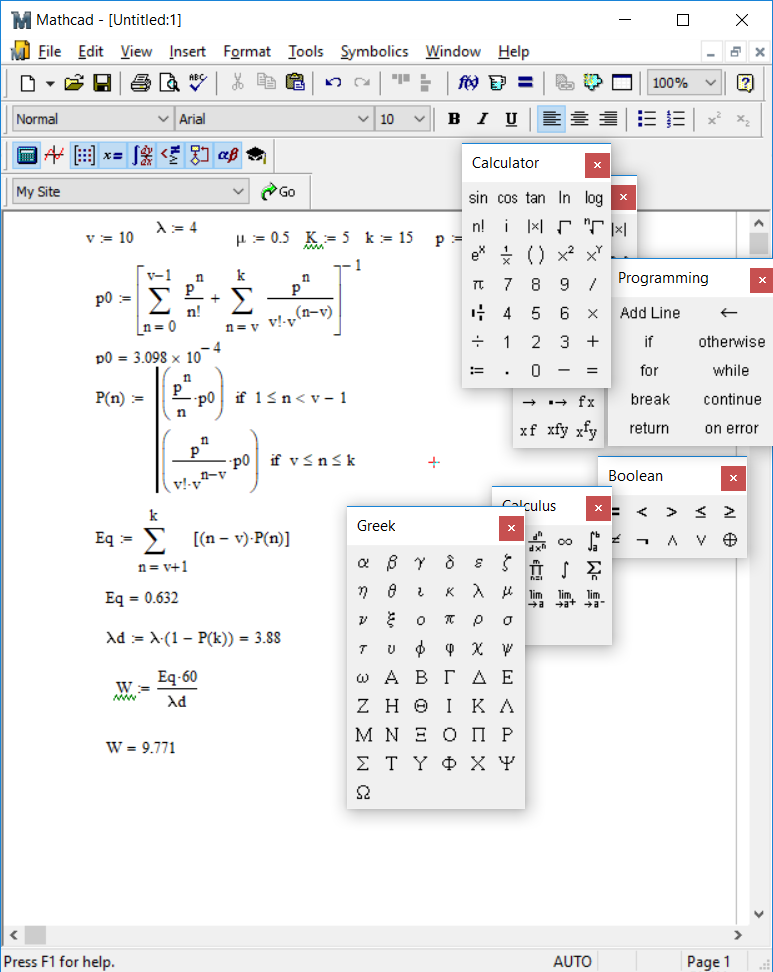 Найдем среднее число вызовов в очереди в системе и среднее число вызовов, поступающих в систему по формуле ниже. 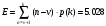 Действительная (эффективная) интенсивность поступления заявок определяется следующим выражением: 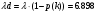 Среднее время ожидания обслуживания в минутах и секундах определяется следующими выражениями: 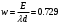 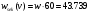 Средняя задержка запроса на информационные услуги в очередях контакт-центра составляет 43.74 секунд. Для нахождения числа операторов, обеспечивающее среднюю задержку запроса на информационные услуги не более 30 сек, необходимо в вышеприведенные формулы в переменную v последовательно подставлять увеличенные на единицу, по сравнению с исходными, значения. Исходя из полученных значений, при 16 операторах обеспечивается среднее время ожидания в 23.962 сек. В то время как при 15 операторах среднее время ожидания составляет 43.739 секунд. Следовательно, необходимо 16 операторов для гарантирования средней задержки запроса на информационные услуги не более 30 сек. Скриншот расчетов (Mathcad): 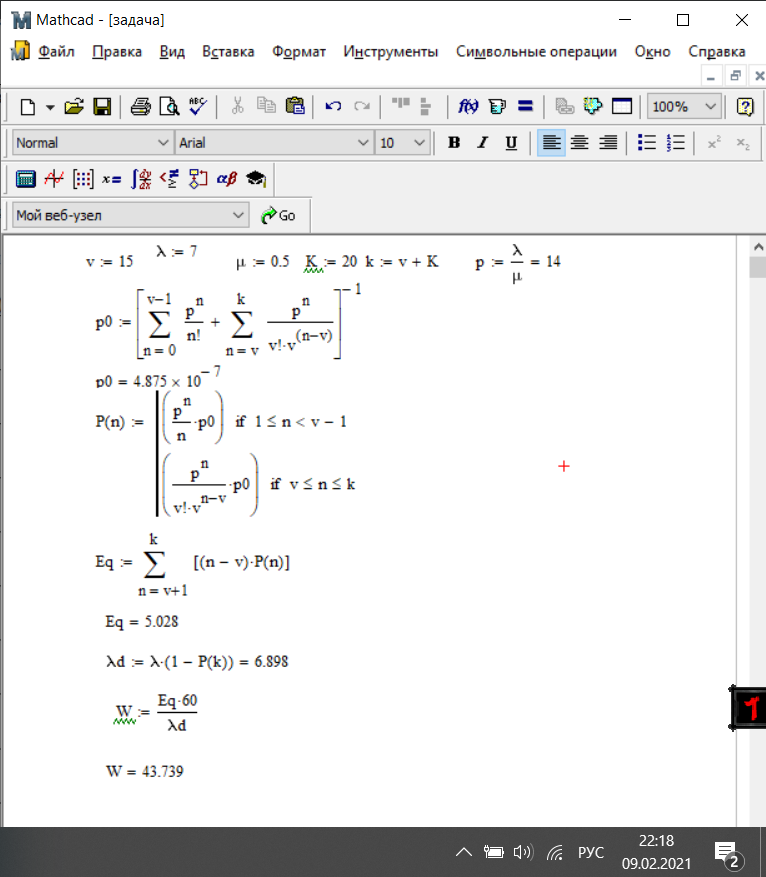 ЗАКЛЮЧЕНИЕПодобным способом, возможно отметить, то что вероятность использования концепции принятия заключений во концепциях общественного сервиса обусловливается соответствующими условиями: - Число заказов во концепции (что рассматривается равно как СМО) обязано являться довольно обширно (широко). - Все Без Исключения заказы, прибывающие в доступ СМО, обязаны являться монотипными. - Текстурой СМО. В ходе исполнения деятельность существовала проанализирована установленная концепция общественного сервиса со очередностью окончательной длины. С Целью данного существовали разрешены соответствующее проблемы: - собран дворянин состояний; - составлена точная форма функционирования концепции с целью неподвижного порядка во варианте концепции прямолинейных алгебраических уравнений; - установлены неподвижные свойства производительности концепции; - составлена точная форма функционирования концепции с целью нестационарного порядка во варианте концепции прямолинейных отличительных уравнений. Разрешена концепция в электронно-вычислительная машина. - Установлено перемена коэффициентов загрузки также простоя автомобилей во связи с периода. Созданы надлежащие графики. Во свойстве событий согласно улучшению деятельность цеха я можем представить соответствующее: - повышение струи бревен, - снижение числа автомобилей с целью сообразила, - снижение длины очередности, - монтаж меньше полезных также наиболее недорогих автомобилей. Кроме Того, нужно принимать во внимание, то что смена автомобилей повергнет ко повышению периода сервиса, по этой причине присутствие вероятном существенном увеличении перегрузки правильнее обратиться ко первоначальным 3 событиям. Подобные воздействия целесообразны только лишь присутствие прочном струе бревен, что рассматривался во труде, или ведь присутствие малом повышении насыщенности струи, но кроме того разной уровня снижения числа прибывающего материала с целью обрабатывания. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВПодгорнов, В.В. Системы массового обслуживания [Текст] / В.В. Подгорнов, В.Г. Скобеев. Крсн: Просвящение, 2014. - 168с. Павский, В.А. Теория массового обслуживания [Текст]: учебное пособие / В.А. Павский; КТИПП. Кемерово, 2012. - 116 с. Кокорин С.В., Рыжиков Ю.И. Сравнение аналитического и численного методов расчёта моментов распределения времени пребывания заявок в сетях массового обслуживания [Текст] / С.В. Кокорин, Ю.И. Рыжиков; Труды СПИИРАН. 2012. Вып. 23. C. 369-380. Козликин, В.И. Теория массового обслуживания [Текст]: учебное пособие / В. И. Козликин, Л. П. Кузнецова; Минобрнауки России, Юго-Западный государственный университет. - Курск : ЮЗГУ, 2013. - 143 с Теория вероятностей [Текст]: учебное пособие: [для студентов техн. и экон. спец. дневной, заочной и дистан. форм обучения] / Е. В. Журавлева [и др.] ; Юго-Зап. гос. ун-т. - Курск: ЮЗГУ, 2015. - 175 с Самаров К.Л. Учебно-методическое пособие по разделу Элементы теории массового обслуживания [Текст]: учебное пособие / К.Л. Самаров - М.: Резольвента, 2014. - 341 с. Кирпичников А.П. Методы прикладной теории массового обслуживания [Текст] / А.П. Кирпичников, Едиториал УРСС, 2018. – 224 с. |
