Курсовая. Курсовая работа Гнездилов Р.Г ИТ-81з. Исследование систем массового обслуживания с ожиданием
 Скачать 1.32 Mb. Скачать 1.32 Mb.
|
1.6 Решение системы дифференциальных уравненийТеперь рассмотрим систему дифференциальных уравнений n-го порядка, которая в общем случае может быть представлена в виде: 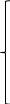 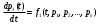 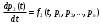 (13) (13)… 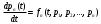 Неизвестными в этой системе являются функции pi(t), i = 1,2,..., n. В момент времени t = 0 значения этих функций известны: 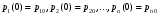 (14) (14)Они образуют начальные условия функционирования системы. Существует большое количество машинных методов решения задачи (13) – (14). Рассмотрим алгоритм самого простейшего метода решения системы дифференциальных уравнений, удовлетворяющего заданным начальным условиям – метода Эйлера. Зададимся шагом h изменения аргумента t . Величину шага можно будет изменять для получения необходимой точности расчетов. Результатом решения системы будет таблица 1 значений функций pi(t), i=1,2,…,n в узлах t=0, t=h, t=2h, …, t=kh=tкон. Здесь tкон – момент времени, до которого ищется решение системы уравнений. Согласно методу Эйлера, таблица 1. заполняется по строкам. Значения вероятностей в 0-й строке известны из начальных условий. Таблица 1 – Результат решения системы
Значения вероятностей в 1-й стоке рассчитываются на основе известных вероятностей 0-й строки по формулам: 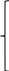 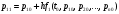 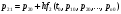 … 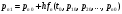 Значения вероятностей во 2-й стоке рассчитываются на основе известных вероятностей 1-й строки по формулам: 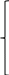 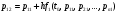 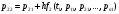 … 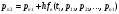 Такой процесс продолжается до тех пор, пока мы не дойдем до последней строки. Значения вероятностей в k-й стоке рассчитываются на основе известных вероятностей предыдущей k - 1-й строки по формулам: 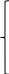 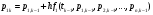 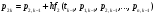 … 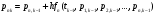 Примечание. Во многих системах дифференциальных уравнений (14) сумма правых частей равна нулю. Таким образом, сумма всех вероятностей для любого момента времени будет постоянной величиной, равной известной сумме начальных вероятностей. В такой ситуации необходимо провести контроль правильности вычислений, суммируя вероятности в каждой строке. Суммы должны быть одинаковы и равны p0. Такое обстоятельство может служить основанием правильности выбора шага интегрирования. |
