Курсовая. Курсовая работа Гнездилов Р.Г ИТ-81з. Исследование систем массового обслуживания с ожиданием
 Скачать 1.32 Mb. Скачать 1.32 Mb.
|
1.7 Коэффициенты загрузки и простоя машин в СМО видаM / M / r / m .Получим формулы для коэффициентов загрузки и простоя банкоматов в зависимости от времени. Число банкоматов, занятых обслуживанием посетителей, есть случайная величина X , закон распределения вероятностей которой приведен в таблица 2. Таблица 2 – Распределение вероятностей числа банкоматов, занятых обслуживанием посетителей
Среднее число таких банкоматов представляет собой математическое ожидание X , рассчитываемое по формуле: 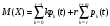 (15) (15)Коэффициент загрузки банкоматов = отношение среднего числа работающих банкоматов к общему числу банкоматов в системе обслуживания, то есть: 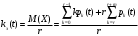 (16) (16)Число свободных банкоматов есть случайная величина Y, закон распределения вероятностей которой приведен в таблице 3. Таблица 3 – Распределение вероятностей числа свободных банкоматов
Среднее число машин, свободных от рубки, представляет собой математическое ожидание Y , рассчитываемое по формуле (17): 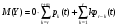 (17) (17)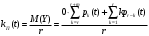 (18) (18)Коэффициент простоя машин равен отношению среднего числа машин, свободных от рубки, к общему числу машин в цехе, то есть формула имеет вид (18) [8]. 2 Практическая частьИсходные данные для анализа системы массового обслуживания содержатся в таблице 4 в соответствии с вариантом №2. Таблица 4 – Данные для анализа системы массового обслуживания
Согласно такой кодировке, рассматриваемая система относится к классу M / M / 2/ 1. 2.1 Граф состоянийВозможные состояния системы: S0 – в системе бревен нет, машины свободны от рубки; S1 – в системе 1 бревно, одна машина занята рубкой; S2 – в системе 2 бревна, две машины заняты рубкой; S3 – в системе 3 бревна, три машины заняты рубкой; S4 – в системе 4 бревна, три машины заняты рубкой, одно бревно находится в очереди. Граф состояний приведен на рисунок 4. Переходы слева направо связаны с поступлением в систему очередного бревна, поэтому интенсивности переходов справа налево одинаковы и равны.  Рисунок 4 – Граф состояний системы M / M / 2 / 1 Переходы справа налево обусловлены окончанием рубки бревна. В состоянии S1 работает одна машина, поэтому интенсивность перехода из состояния S1 в состояние S0.В состояниях S2, S3 и S4 работает две, три и три машины соответственно, поэтому соответствующие интенсивности переходов умножаются на 2, 3. Данный граф описывает процесс размножения и гибели и для него справедливы все соотношения п.1.4. Тем не менее, мы получим данные соотношения еще раз непосредственно по графу состояний [9]. |
