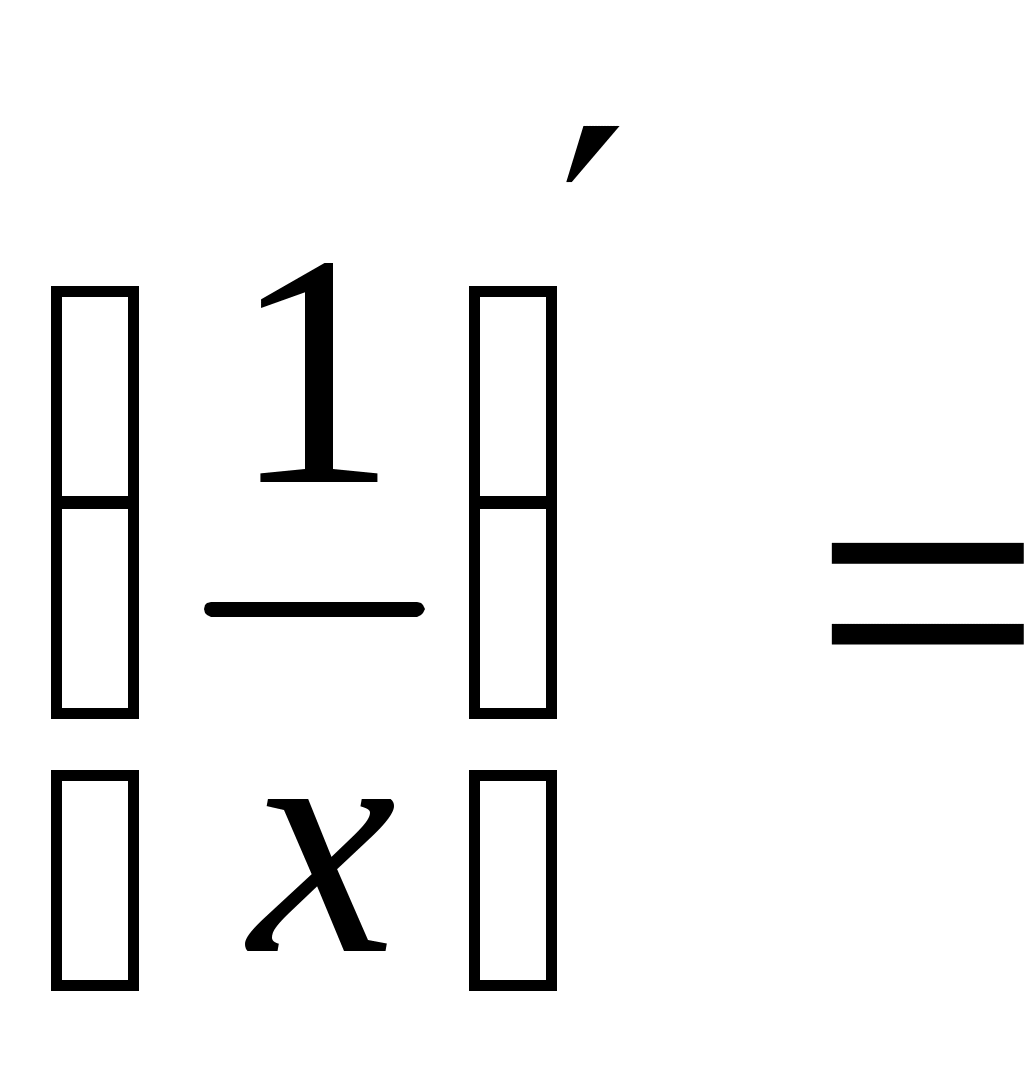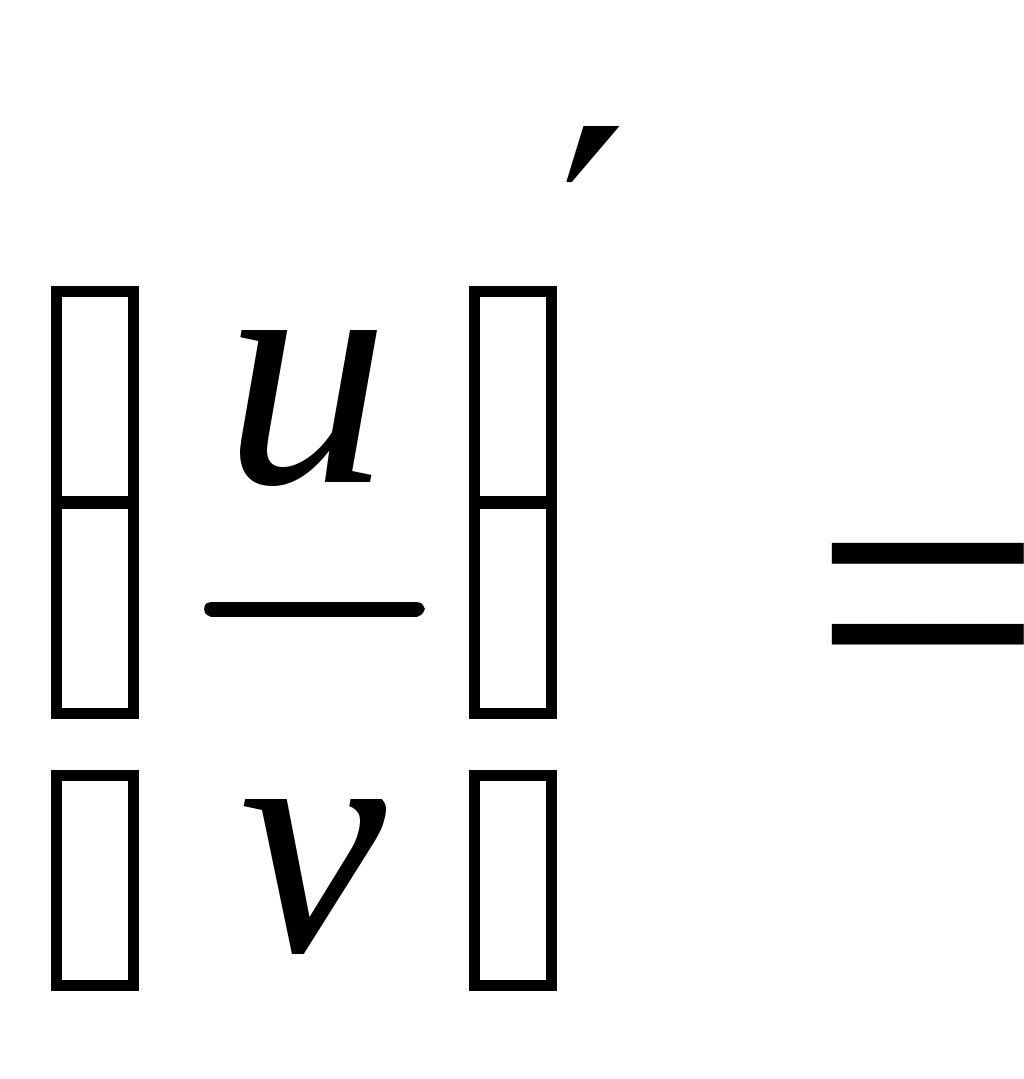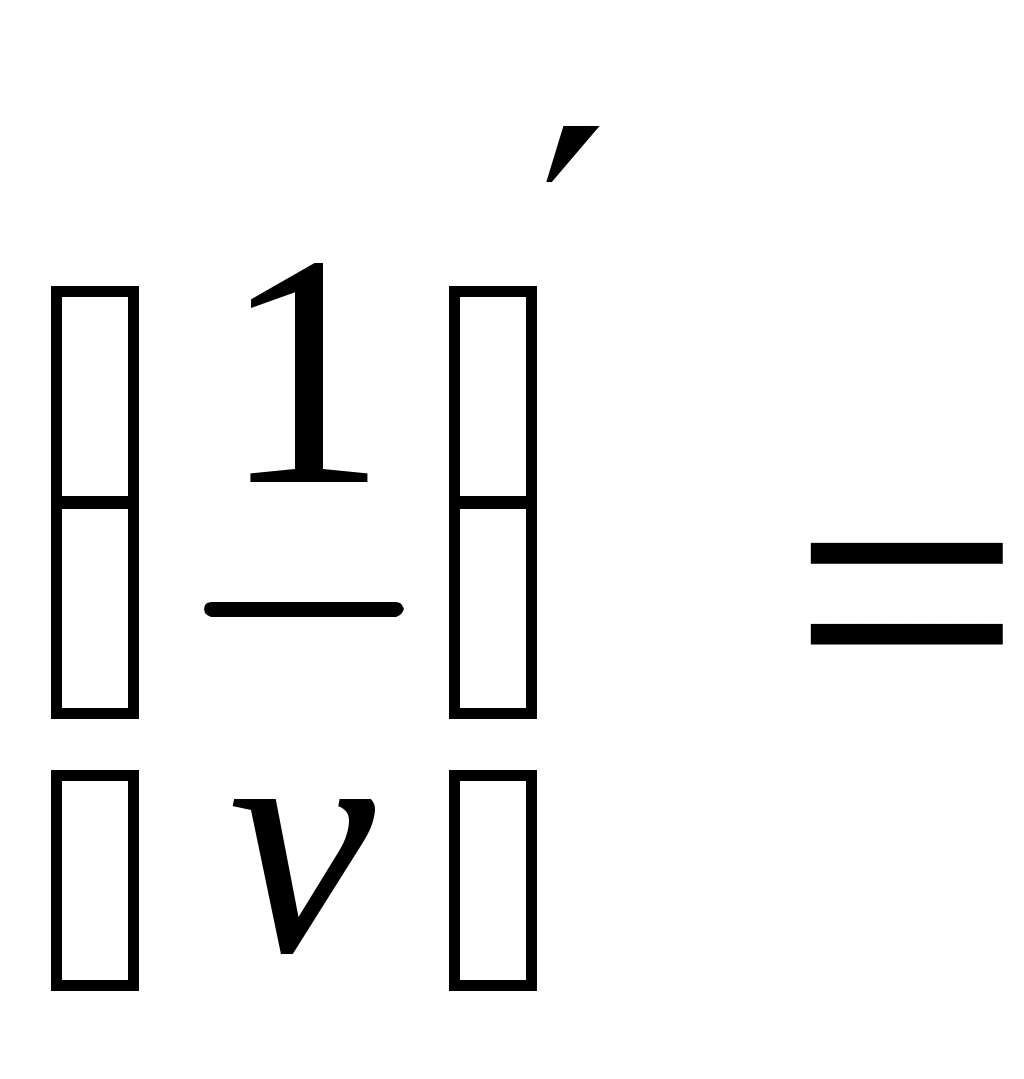КОС ЕН.01 математика 10.02.05.docx. Комплект оценочных средств для проведения текущего контроля успеваемости и промежуточной аттестации в форме дифференцированного зачета по учебной дисциплине ен. 01 Математика
 Скачать 1.37 Mb. Скачать 1.37 Mb.
|
|
Раздел 4. Дифференциальное исчисление Самостоятельная работа. Вариант 1 Найти производную функции Найти производную третьего порядка функции Написать уравнение касательной к графику функции Материальная точка движется по закону Вариант 2 Найти производную функции Найти производную третьего порядка функции Написать уравнение касательной к графику функции Материальная точка движется по закону Вариант 3 Найти производную функции Найти производную третьего порядка функции Написать уравнение касательной к графику функции Материальная точка движется по закону Вариант 4 Найти производную функции Найти производную третьего порядка функции Написать уравнение касательной к графику функции Материальная точка движется по закону Вариант 5 Найти производную функции Найти производную третьего порядка функции Написать уравнение касательной к графику функции Материальная точка движется по закону Вариант 6 Найти производную функции Найти производную третьего порядка функции Написать уравнение касательной к графику функции Материальная точка движется по закону За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл. За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов. Устный ответ Сформулировать правила дифференцирования и записать производные основных элементарных функций:
Самостоятельная работа. Текст задания Исследовать функцию и построить ее график. Вариант 1 Вариант 2 Вариант 3 Вариант 4 Вариант 5 Вариант 6 Вариант 7 Вариант 8 Расчётное задание Вариант 1 Найти производную функции Вариант 2 За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл. За неправильный ответ на вопросы или неверное решение задачи выставляется – 0 баллов. Расчетное задание Вариант 1 1) Найти промежутки возрастания и убывания для функций: а) y=x2-8x+12 б) y=x3-6x2+4 в)y= ln x2 г) y= 2) Исследовать на экстремум: a) y=x2-4x ; б) y=x3-3x2 ; 3) Найти точки перегиба: а) y=x3-x ; б) y=x+ Вариант 2: 1) Найти промежутки монотонности следующих функций: а) f(x)=x2-6x+5 ; б) f(x)=x3-3x2+1 ; в) y=ln ; г) y= 2) Исследовать на экстремум: а) y=-x2+5x б)y=0,5x4 в) y=x2-8x+12 3) Найти точки перегиба: a) y=6x2-x3 б) y= x3-3x2+8x-4 За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл. За неправильный ответ на вопросы или неверное решение задачи выставляется – 0 баллов. Расчетное задание Вариант 1 Исследовать функции и построить графики: 1). y= х / (х-3) 2). y=(x-1) 3). y= -х/2 + arctgx Вариант 2 Исследовать функции и построить графики: 1). y= √ 1-соs х За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл. За неправильный ответ на вопросы или неверное решение задачи выставляется – 0 баллов Раздел 5. Интегральное исчисление Текст задания Вариант 1 Найти неопределенные интегралы методом непосредственного интегрирования (для № 1-5). 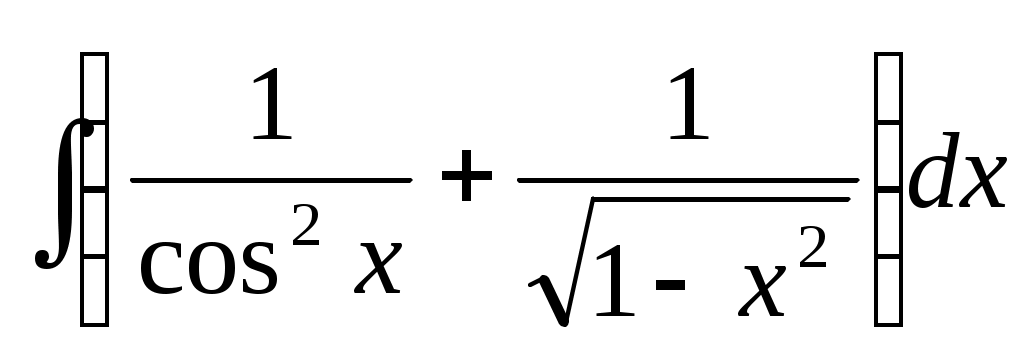 . .Найти неопределенные интегралы методом подстановки (для № 6-8). Найти неопределенный интеграл методом интегрирования по частям: Вариант 2 Найти неопределенные интегралы методом непосредственного интегрирования (для № 1-5). Найти неопределенные интегралы методом подстановки (для № 6-8). Найти неопределенный интеграл методом интегрирования по частям: За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл. За неправильный ответ на вопросы или неверное решение задачи выставляется отрицательная оценка – 0 баллов. Устный ответ Текст задания Записать табличные интегралы: 1о. 2о. В частности, 3о. 4о. В частности, 5о. 6о. 7о. 8о. 9о. В частности, 10о. В частности, Текст задания Вариант 1 Вычислить определенный интеграл: 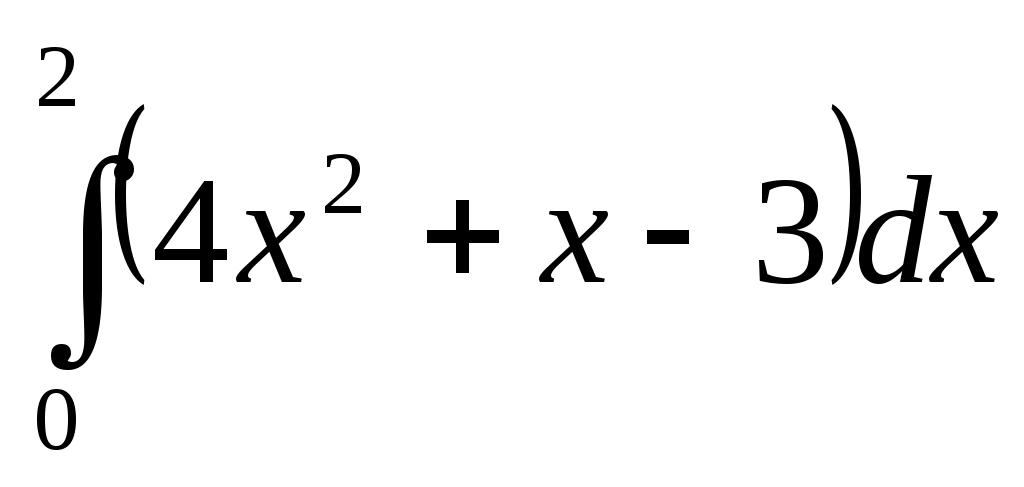 . .Вычислить определенный интеграл методом подстановки: 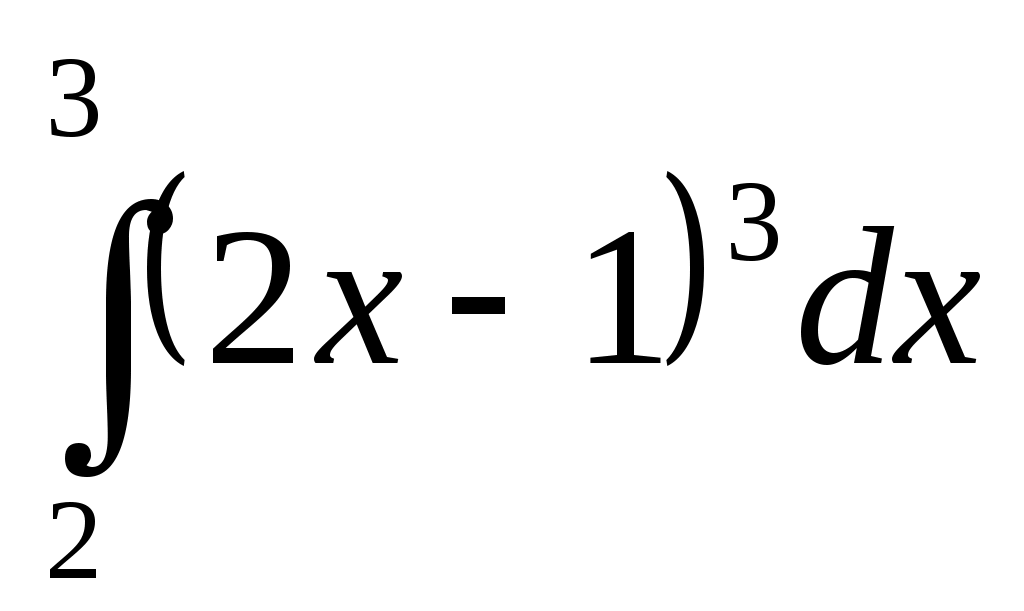 . .Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями: Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями: Скорость движения точки изменяется по закону Вариант 2 Вычислить определенный интеграл: 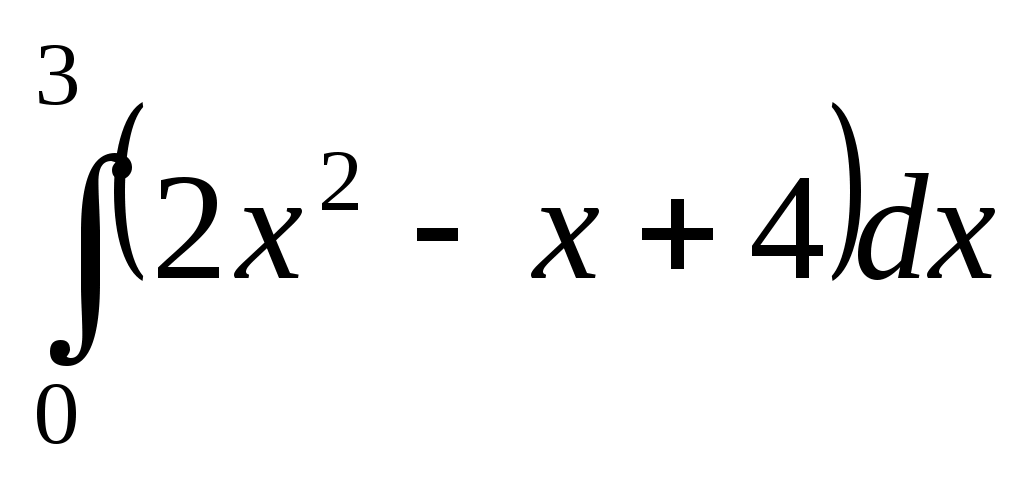 . .Вычислить определенный интеграл методом подстановки: 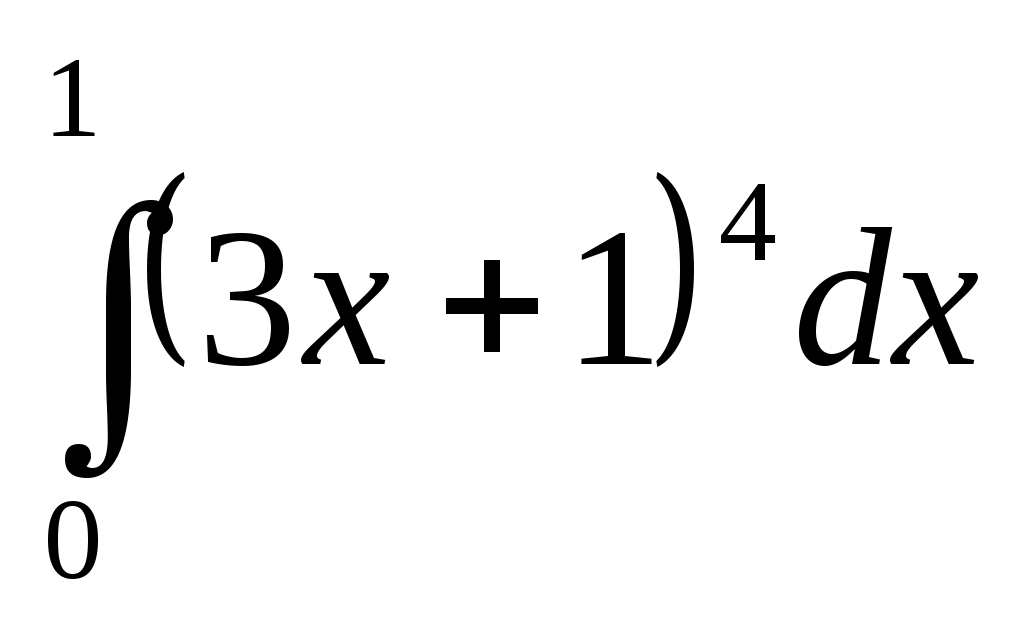 . .Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями: Найти объем тела, полученного при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями: Скорость движения точки изменяется по закону Вариант 1 Найти частные производные функций. Вариант 2 Найти частные производные функций. Расчетное задание Вариант 1 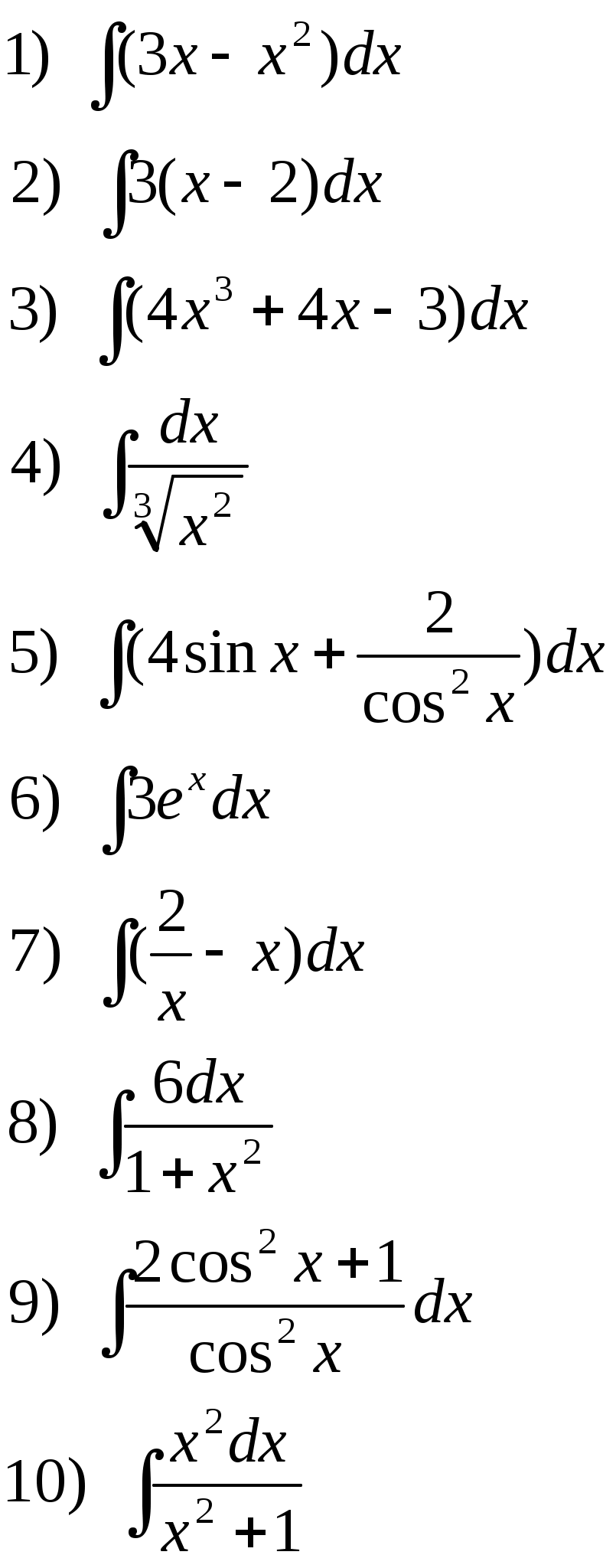 Вариант 2 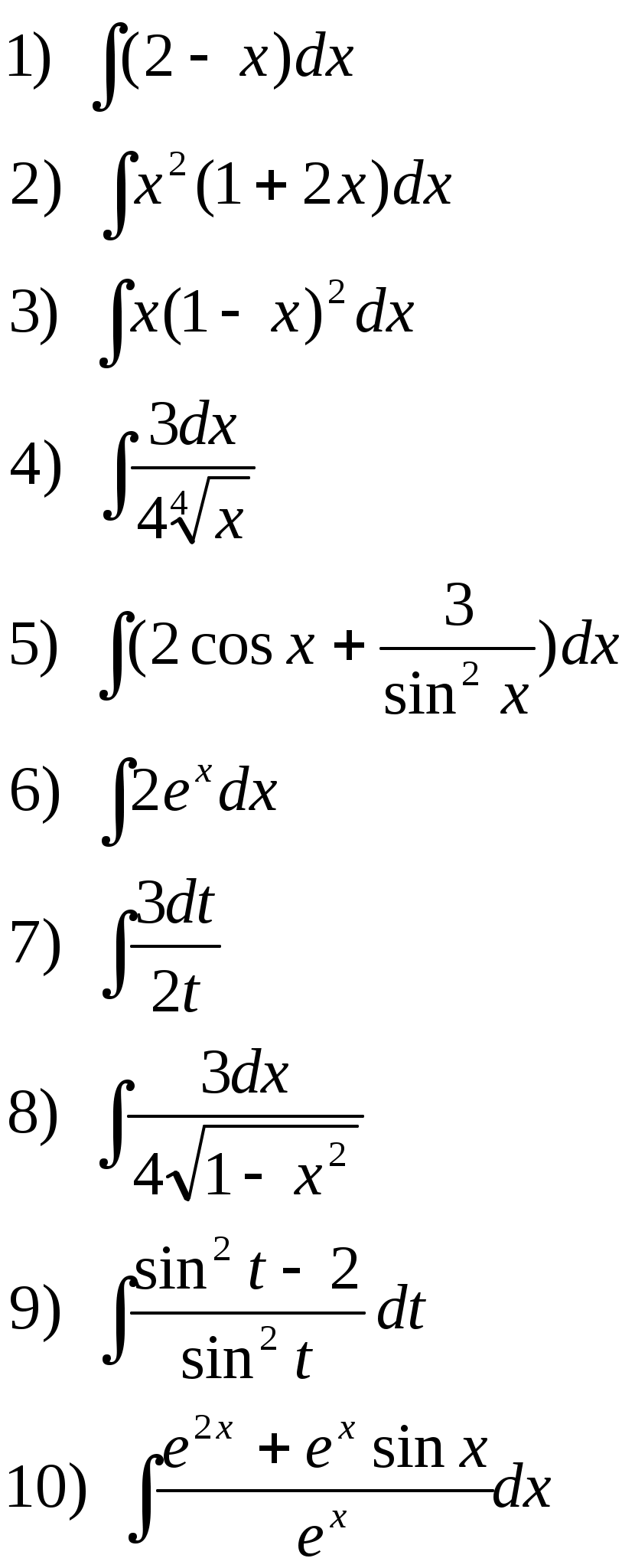 За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл. За неправильный ответ на вопросы или неверное решение задачи выставляется – 0 баллов Расчетное задание Вычислить интегралы способом подстановки. Вариант 1 Вариант 2 За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл. За неправильный ответ на вопросы или неверное решение задачи выставляется – 0 баллов Расчётное задание Вариант 1 Вариант 2 За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл. За неправильный ответ на вопросы или неверное решение задачи выставляется – 0 баллов Расчетное задание Вариант 1 1) 2) 3) 4) Вариант 2 1 2) 3) 4) За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл. За неправильный ответ на вопросы или неверное решение задачи выставляется – 0 баллов Расчетное задание Интегрирование тригонометрических функций. Вариант 1 1) 2) 3) 4) 5) Вариант2: 1) 2) 3) 4) 5) За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл. За неправильный ответ на вопросы или неверное решение задачи выставляется– 0 баллов. Расчетное задание Интегрирование иррациональных функций. Вариант 1 1) Вариант 2 1) За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл. За неправильный ответ на вопросы или неверное решение задачи выставляется – 0 баллов. Расчетное задание Определённый интеграл (непосредственное интегрирование) Вариант 1. 1) 2) 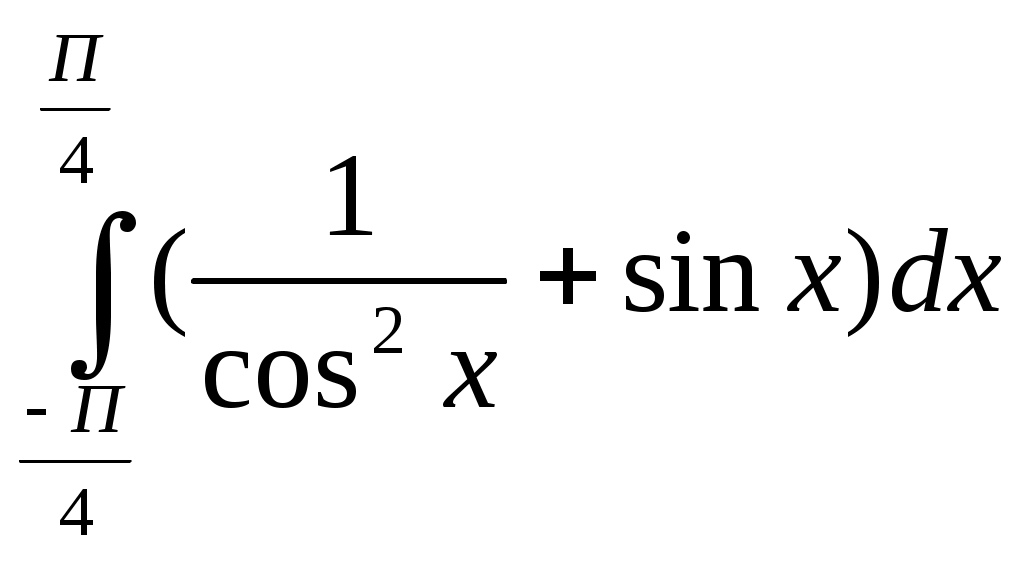 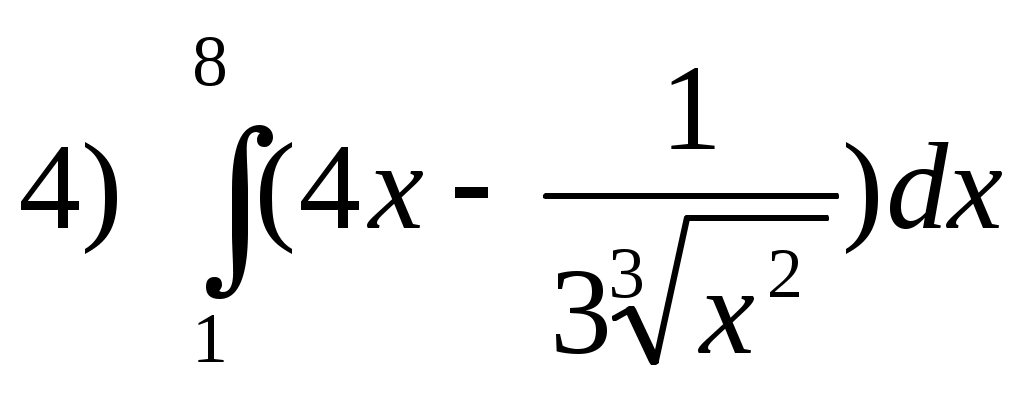 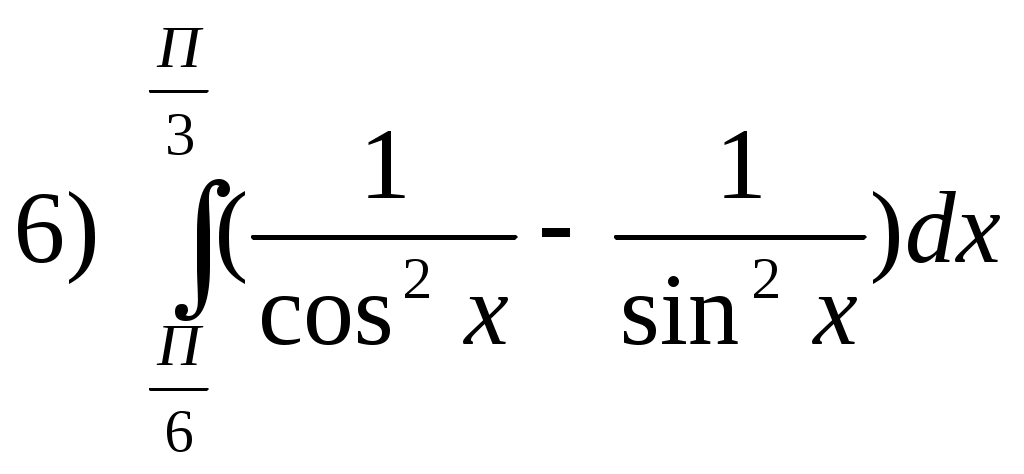 Вариант 2 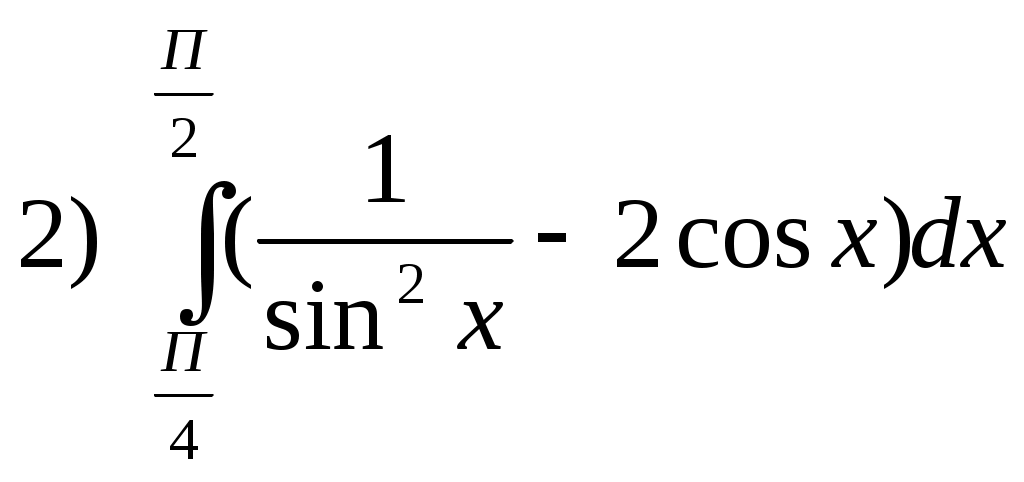 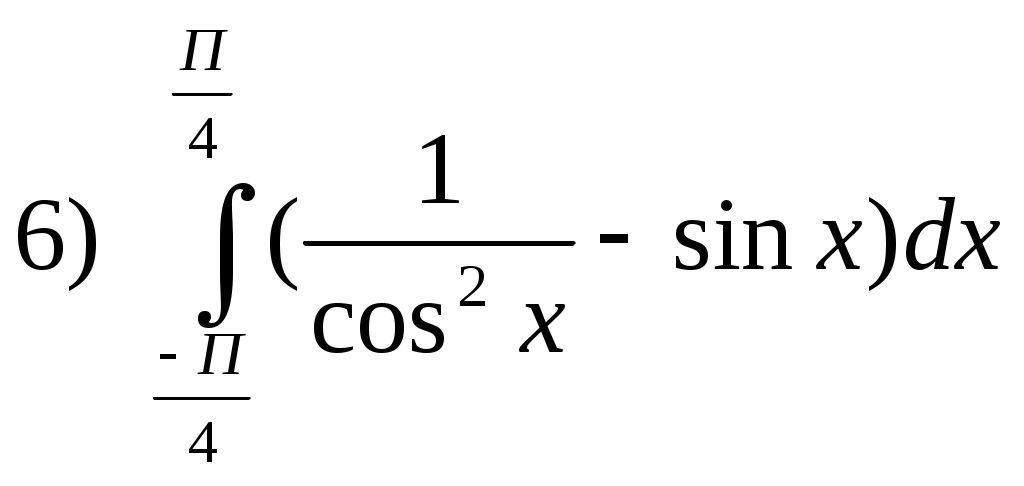 За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл. За неправильный ответ на вопросы или неверное решение задачи выставляется – 0 баллов. Расчетное задание Вычислить определённый интеграл способом подстановки. Вариант 1 Вариант 2 9) За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл. За неправильный ответ на вопросы или неверное решение задачи выставляется – 0 баллов. Расчетное задание Вариант 1. Найти площадь, ограниченную линиями: y = -x2+9 и y=0 y = x2 и y = 2x+3 y = , y = 0, x = 1, x = 5 4) y=x2-8x+16, x+y-6=0 5) y= x3 , y=2x 6) y=cos x, y=0, x=0, x= 7) y2=x; y≥0; x=1; x=4 8) y= -x2-2x+3, x=0, x=2, y=0 9) y=3+2x-x2, y=x+1 10) y=x2+3, xy=4, y=2, x=0 Вариант 2. Найти площадь, ограниченную линиями: y = -x2+16 и y=0 y=x2 и y=4x-3 y= , y=0, x=1, x=6 y=x2-4x+5, x-y+5=0 y2=2x и x2=2y y= sin x, y=0, x= , x=π y= -6x; y=0; x=4 y= x3; y=0; x=-1; x=2 y=x2+4x и y=x-y+4 y=4-x2, y=x2-2x, y=0 (фигура расположена во второй четверти) За правильный ответ на вопросы или верное решение задачи выставляется положительная оценка – 1 балл. За неправильный ответ на вопросы или неверное решение задачи выставляется – 0 баллов. | ||||||||||||||||||||||||||||||||||||||||||