КОС ЕН.01 математика 10.02.05.docx. Комплект оценочных средств для проведения текущего контроля успеваемости и промежуточной аттестации в форме дифференцированного зачета по учебной дисциплине ен. 01 Математика
 Скачать 1.37 Mb. Скачать 1.37 Mb.
|
|
Шкала оценки образовательных достижений
2.3Задания для дифференцированного зачета Теоретические вопросы по дисциплине ЕН.01 Математика Матрицы, действия над матрицами. Определители 1-го, 2-го, 3-го порядков. Правило треугольников. Определители n-го порядка. Теорема Лапласа. Обратная матрица. Алгоритм нахождения обратной матрицы. Ранг матрицы. Алгоритм вычисления ранга матрицы с помощью элементарных преобразований. Система линейных уравнений. Метод обратной матрицы. Формулы Крамера. Метод Гаусса. Предел функции в точке. Основные теоремы о пределах. Предел функции при x, стремящемся к бесконечности. Замечательные пределы. Число е. Непрерывность функции в точке и на промежутке. Точка непрерывности функции. Точка разрыва функции. Свойства непрерывных функций. Приращение аргумента. Приращение функции. Производная функции. Дифференциал функции. Геометрический смысл производной. Механический смысл производной. Таблица производных. Понятие сложной функции. Производная сложной функции. Производные высших порядков. Физический смысл второй производной. Исследование функции с помощью второй производной. Первообразная. Неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица неопределенных интегралов. Методы интегрирования: метод непосредственного интегрирования; метод замены переменной (метод подстановки); метод интегрирования по частям. Определенный интеграл. Понятие интегральной суммы. Достаточное условие существования определенного интеграла (интегрируемости функции). Основные свойства определенного интеграла. Геометрический смысл определенного интеграла. Методы вычисления определенных интегралов. Формула Ньютона-Лейбница. Геометрические и физические приложения определенного интеграла. Функции нескольких переменных. Частные производные. Понятие дифференциального уравнения. Общее и частное решение дифференциального уравнения. Интегральные кривые. Задача Коши. Задачи, приводящие к дифференциальным уравнениям. Методы решения дифференциальных уравнений. Понятие числового ряда. Сходимость и расходимость числовых рядов. Необходимый признак сходимости ряда. Признак сравнения. Признак Даламбера. Понятие знакочередующегося ряда. Признак сходимости Лейбница. Абсолютная и условная сходимость знакопеременного ряда. Функциональные ряды. Степенные ряды. Область сходимости степенного ряда. Разложение элементарных функций в ряд Маклорена. Понятие события. Достоверные, невозможные, совместные, несовместные, противоположные события. Классическое определение вероятности. Теорема сложения вероятностей. Теорема умножения вероятностей. Случайная величина. Дискретная и непрерывная случайные величины. Закон распределения дискретной случайной величины. Интегральная функция распределения непрерывной случайной величины. 36. Математическое ожидание дискретной случайной величины. Отклонение случайной величины. Дисперсия дискретной случайной величины. Среднее квадратичное отклонение случайной Перечень практических заданий: Вычислить предел 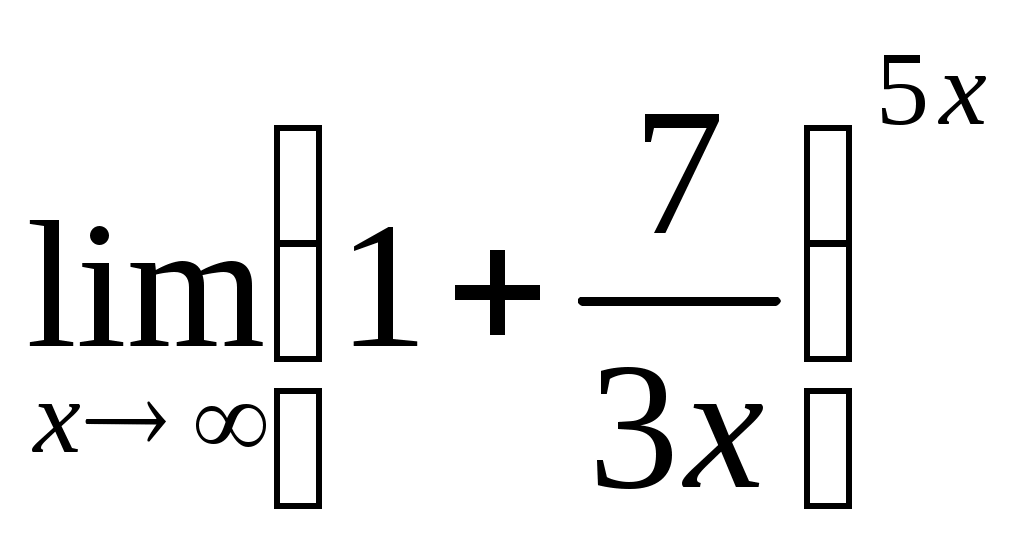 . .Вычислить пределы: а) Вычислить предел Вычислить предел Вычислить предел Вычислить предел Исследовать функцию Исследовать функцию Вычислить значение производной следующих функций в точке а) Найти производную функции Найти производную функции Найти производную функции Найти производную функции Найти неопределенный интеграл Найти неопределенный интеграл методом замены переменной Найти неопределенный интеграл методом замены переменной Найти неопределенный интеграл методом замены переменной Найти неопределенный интеграл методом замены переменной Вычислить определенный интеграл 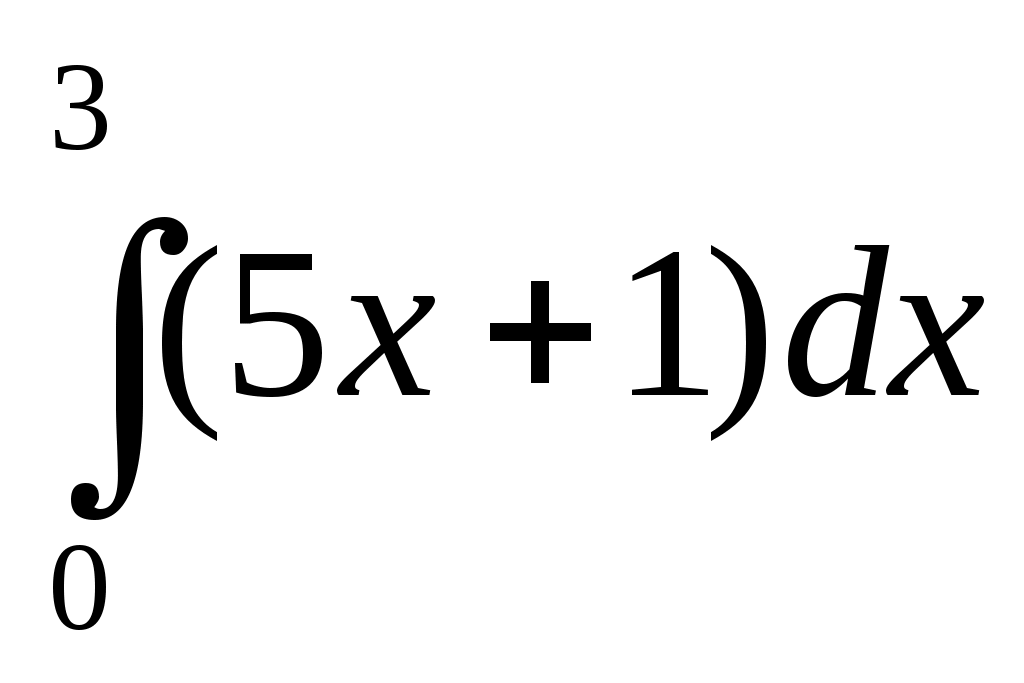 . .Вычислить определенный интеграл 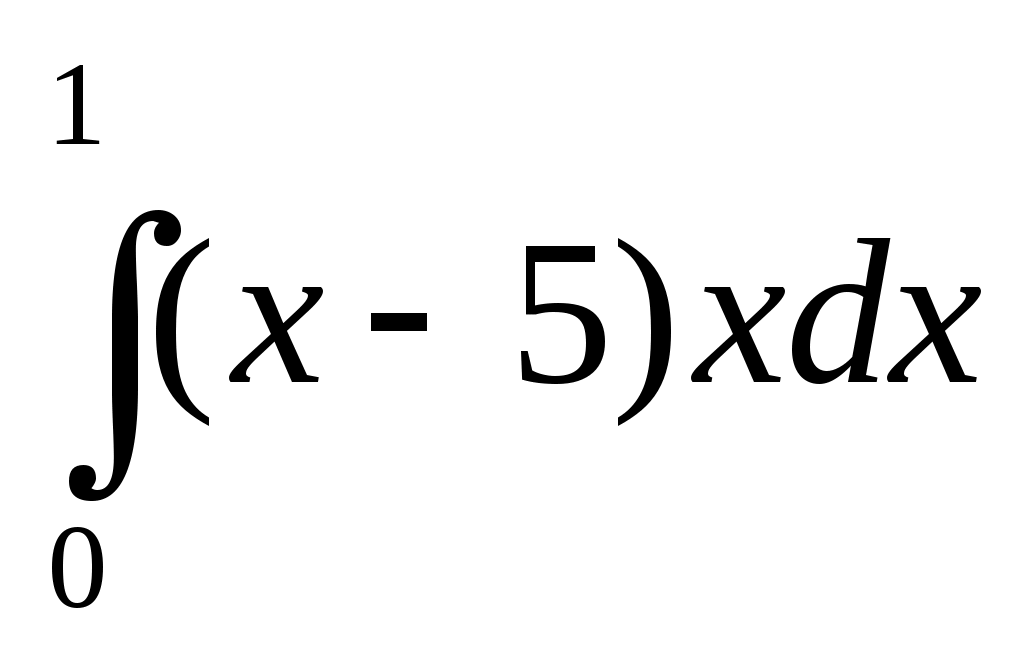 . .Вычислить определенный интеграл 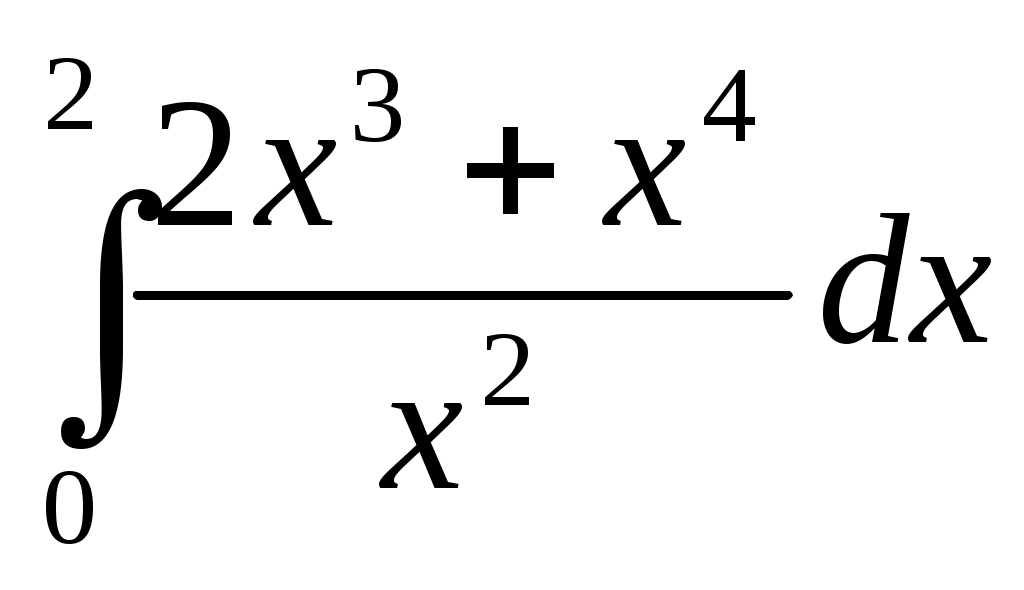 . .Скорость движения точки изменяется по закону Вычислить объем тела, полученного от вращения фигуры, ограниченной линиями Вычислить площадь фигуры, ограниченной линиями Решить дифференциальное уравнение Решить задачу Коши: Решить дифференциальное уравнение В одной корзине находятся 5 белых и 10 черных шаров, в другой – 4 белых и 11 черных. Из каждой корзины вынули по шару. Найти вероятность того, что оба шара окажутся черными. В лотерее 1000 билетов. Разыгрывается один выигрыш в 200 рублей и десять выигрышей по 100 рублей. Пусть Х – величина возможного выигрыша для человека, имеющего один билет. Составить закон распределения этой случайной величины Х. Случайная величина Х задана законом распределения:
Найти математическое ожидание, дисперсию, среднее квадратичное отклонение этой случайной величины Х. 2.4. Пакет экзаменатора
Условия выполнения заданий: Время выполнения задания: 120 мин. Оборудование: бумага, ручка. РЕЦЕНЗИЯ на комплект оценочных средств, для проведения текущего контроля знаний и промежуточной аттестации в форме дифференцированного зачёта по учебной дисциплине ЕН.01 Математика в рамках программы подготовки специалистов среднего звена по специальности 10.02.05 Обеспечение информационной безопасности автоматизированных систем, выполненный преподавателем ГБПОУ КК АЮТ Волкодамовой О.А. Данный комплект оценочных средств (далее - КОС) предназначен для контроля качества обучения дисциплины ЕН.01 Математика в учреждении среднего профессионального образования, реализующем федеральный государственный образовательный стандарт среднего профессионального образования в рамках программы подготовки специалистов среднего звена (далее – ППССЗ) по специальности 10.02.05 Обеспечение информационной безопасности автоматизированных систем. КОС, в соответствии с рабочей программой курса, включает в себя задания для проведения текущего и промежуточного контролей знаний обучающихся о значении математики в профессиональной деятельности и при освоении ППССЗ, основных математических методов решения прикладных задач в области профессиональной деятельности, основных понятий и методов математического анализа, дискретной математики, линейной алгебры, основ интегрального и дифференциального исчисления и умения решать прикладные задачи в области профессиональной деятельности, а также формирования общих и профессиональных компетенций, предусмотренных ФГОС СПО по данной специальности. Содержание КОС в первую очередь предполагает формирование практических умений по применению основных методов математических расчётов, т.к. базируется на компетенциях, которыми должен обладать обучающийся при изучении общепрофессиональных дисциплин и профессиональных модулей по данной специальности. Соблюдена преемственность изучения учебной дисциплины ЕН.01 Математика по отношению к рабочей программе базовой дисциплины ПД.01 Математика: алгебра и начала математического анализа; геометрия. Содержание дисциплины позволяет неоднократно возвращаться к знакомому материалу на новом уровне, продолжая формировать систему общих и профессиональных компетенций. В процессе изучения дисциплины преподавателю предоставляются широкие возможности для использования современных форм организации обучения и контроля знаний и умений обучающихся, основной упор при этом делается на развитие навыков самостоятельной работы и самоконтроля с помощью информационных технологий. Данные контрольно-оценочные средства соответствуют требованиям ФГОС СПО и рекомендуются для использования в учреждениях среднего профессионального образования. Рецензент: Макуха И.А., преподаватель ГБПОУ КК «Армавирский юридический техникум» (личная подпись) М.П. «___»___________201__г. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
