Конспект лекций основы гидро и пневмо приводов. Осн.гидропр. Консп.. Конспект. Часть Гидропривод Введение Гидравлика наука о жидкостях, законах их равновесия и движения
 Скачать 0.75 Mb.
|
|
Основы гидропривода и пневмопривода Конспект. Часть 1. Гидропривод Введение Гидравлика-наука о жидкостях, законах их равновесия и движения. Гидростатика изучает законы равновесия жидкости. Гидродинамика изучает законы движения жидкости, законы ее взаимодействия с другими жидкостями и твердыми телами. Законами поведения жидкостей занимались еще в древние века. Известны работы, связанные с жидкостями, в древнем Египте, Китае, Турции. Известный нам закон с названием «закон Архимеда» был опубликован ученым за 250 лет до н.э. в трактате «О плавающих телах». В эпоху возрождения были заново открыты или использовались известные в древности сведения. Леонардо да Винчи, осуществивший открытия и изобретения практически во всех науках, вывел и использовал общетехнические принципы гидравлики и пневматики. Известны работы Ломоносова, Эйлера, Бернулли разработавшие законы, приведшие гидравлику к уровню инженерного использования, т.е. позволившие производить расчеты гидравлических устройств. В 18—19 веках учеными было много сделано, чтобы гидравлические законы были описаны математическими соотношениями, которые можно было бы использовать для проектирования гидравлических систем. К ним относятся такие ученые, как Тито, Рейнольдс, Жуковский и др. , имена которых носят известные законы гидравлики. В наше время гидропривод наряду с электроприводом широко применяется во всех отраслях науки и техники. Особенность его заключается в том, что исполнительные устройства гидропривода при малых габаритах создают большие усилия. Механизмы на основе гидропривода обладают простотой кинематических цепей. Это приводит зачастую к вытеснению гидроприводом других видов привода. Часто используют комбинированные приводы, сочетающие в себе достоинства различных приводов. 1.Гидравлические приводы 1.1 Основы машиностроительной гидравлики 1.1.1 Рабочие жидкости Жидкости характеризуются следующими параметрами. 1 Плотность ρ =  , наименование [ρ] = 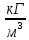 Плотность измеряют ареометрами. Плотность воды ρводы = 1000 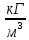Плотность бензина ρбенз =890 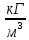Плотность зависит от температуры. Часто в ареометр встраивают термометр и изображают график зависимости плотности от температуры. 2 Удельный вес γ =  =  = ρg, наименование [γ] =  .3  Вязкость это свойство жидкости оказывать сопротивление относительному перемещению слоев жидкости. Различают динамическую вязкость и кинематическую вязкость. Скорости слоев различны. Более быстрые слои увлекают частицы более медленных и наоборот: медленные тормозят быстрые. Между слоями возникает касательная (направленная вдоль слоев) сила трения Т. Напряжение трения τ =  , где S—площадь соприкосновения слоев. Для определения понятия вязкость вводят понятие градиент скорости grad υ=  = 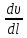1- 1)Δl→0 Градиент скорости показывает, как изменяется скорость в направлении поперек линий перемещения жидкости. По закону, выведенному Ньютоном, касательная сила Т пропорциональна площади S соприкосновения трущихся слоев и градиенту скорости: Т = μSgradυ 1- 2) μ—коэффициент пропорциональности, показывающий степень зависимости силы трения от изменения скорости слоев в жидкости. Коэффициент μназывается динамической вязкостью жидкости. Чем больше динамическая вязкость, тем больше затягиваются слои друг другом; динамическая вязкость характеризует силы касательного трения между слоями. Наименование единицы динамической вязкости можно вывести из 2): [μ] = 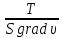 = =Па = Па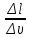 = Па.сКинематической вязкостью ν называется отношение динамической вязкости μжидкости к ее плотности ρ : ν =  . Наименование [ν] =  = =  = .Старая единица измерения кинематической вязкости – Стокс (Ст). 1Ст = 10-4 .Вязкость с увеличением температуры уменьшается нелинейно. Вязкость с увеличением давления увеличивается. Вязкость жидкости с растворенным газом уменьшается. Измеряется вязкость приборами, называемыми вискозиметрами. 4 Сжимаемость жидкости характеризуется модулем объемного сжатия Е: Е = - 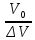 Δp 1-3)где V0 – первоначальный объем, ΔVизменение объема при изменении давления на Δр. Наименование сжимаемости –Па. Знак «- » в выражении 3) говорит об уменьшении объема при увеличении давления. В статических расчетах сжимаемостью можно пренебречь, жидкость считается несжимаемой. 5 Тепловое расширение жидкости определяется выражением V = V0(1 + βΔt), где V0—первоначальный объем жидкости, β – температурный коэффициент объемного расширения. Для минеральных жидкостей Е ≈ 1470 МПа, β ≈ 7.10-4  6 Идеальная жидкость это жидкость, которая абсолютно несжимаема и в которой отсутствуют силы внутреннего трения. Законы, выведенные для идеальной жидкости, для реальной жидкости корректируют. 1.1.2 Гидростатика. Законы гидростатики. Силы, действующие на жидкость, принято делить на внешние (действуют со стороны тел, окружающих жидкость) и внутренние. Внутренние силы являются силами взаимодействия между минимальными объемами внутри жидкости. Внешние силы разделяются на поверхностные и массовые. Поверхностные силы приложены к поверхности выделенного объема жидкости (например, давление). Массовые силы действуют на все элементарные объемы жидкости, образующие рассматриваемый объем (например, вес, центробежная сила). Действие силы на жидкость характеризуется давлением p. р = 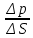 при Δs→0 (Δр-величина силы, действующей на площадку ΔS). Рассматривают давление нормальное р (сила действует нормально к площадке ΔS) итангенциальное τ (сила действует касательно к площадке). Касательное напряжение τвызывает движение одних слоев жидкости относительно других, перемешивание жидкости. Наименование нормального и тангенциального давлений 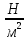 .Основное уравнение гидростатики Н  а жидкость действует внешнее давление р0. Каково будет давление рм в точке М на глубине h?На элементарной площадке Δs, взятой вокруг точки М мысленно построен прямой цилиндр высотой h. Действие жидкости на мысленно построенный цилиндр можно заменить силами. На цилиндр действуют следующие силы. 1) Сила внешнего давления Р0= р0 Δs; 2)Сила тяжести жидкости в цилиндре G = ρghΔs; 3) Сила, действующая на цилиндр со стороны жидкости снизу F= ржΔs, где рж – давление на глубине h в жидкости; 4) Силы действующие на боковые поверхности цилиндра. Силы, действующие на боковые поверхности цилиндра, уравновешены: иначе жидкость смещалась бы и перемешивалась. Их можно не учитывать. Остальные силы уравновешивают друг друга и Р0+ G= F ржΔs=ρghΔs+р0Δs. После сокращения наΔsостается выражение, которое называется основным уравнением гидростатики: рж = р0 +ρgh, 1-4) которое словами выражается следующим образом: Полное давление жидкости (гидростатическое давление) в любой точке жидкости, находящейся в покое, равно сумме внешнего давления р0 и давления ρgh, вызванного силой тяжести столба жидкости над рассматриваемой точкой. М 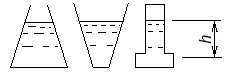 ожно показать, что на данной глубине давление во всех направлениях одинаково и равно рж. Этим же объясняется то, что давление внутри жидкости не зависит от формы емкости, в которой она находится, а зависит лишь от глубины h.Закон Паскаля является следствием выражения 1-4), из которого видно, что давление на глубине h обусловлено двумя составляющими: внешним давлением р0 и давлением, обусловленном глубиной h. Из выражения видно, что внешнее давление р0 передается во все точки жидкости одинаково. Закон Паскаля формулируется следующим образом: Внешнее давление передается во все точки жидкости и по всем направлениям одинаково. Н  а законе Паскаля основана работа гидропрессов, гидропреобразователей и гидроаккумуляторов.Гидропресс. Так как внешнее давление во всех точках жидкости одинаково, под обоими поршнями давление р. Для большего поршня р =  . Для меньшего р=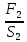 . Вследствие равенства давлений =  За счет разной площади поршней можно п олучить увеличение силы: F2 = F1 .Гидропреобразователь. Поршни связаны штоком. Поэтому си -лы F на них одинаковы. F = p1S1 = p2S2. Давление в правой области усиливается по сравнению с левой во столько раз, во сколько площадь S1 больше площадиS2: р2 = р1  .Закон Архимеда определяет силу, выталкивающую тело, погруженное в жидкость. Внутри жидкости выделен параллелепипед с с площадью верхней и нижней граней S. На верхнюю грань действует сила F1= ρgh1S. Н  а нижнюю грань действует сила F2= ρgh2S. Выталкивающая сила F= F2- F1= ρgh2S - ρgh1S =ρg(h2 – h1)S= ρgV, где V=(h2 – h1)S—объем выделенного параллелепипеда. F= ρgV 1-5) ρgV в выражении 1-5) представляет собой вес выделенного объема. Закон Архимеда говорит о том, что сила, выталкивающая погруженное в жидкость тело, равна весу жидкости в объеме тела. Иногда говорят: весу вытесненной телом жидкости, что равносильно. Если вес тела, погруженного в жидкость, больше выталкивающей силы, тело тонет, меньше—всплывает, равно—положение безразлично. Выталкивающая сила не зависит от глубины погружения! 1.1.3 Гидродинамика. Основные понятия 1 Установившееся и неустановившееся движение жидкости. Установившимся движением жидкости называется такое движение, при котором скорость и давление в каждой точке постоянны и являются функциями координат этой точки: υ = υ (x,y,z), p =p(x,y,z). При неустановившемся движении эти характеристики меняются от времени: υ = υ (x,y,z,t), p =p(x,y,z,t). 2 Напорное и безнапорное движение жидкости При напорном движении жидкость со всех сторон окружена стенками (трубы). При безнапорном – верхняя стенка отсутствует (река, ручей). 3  Принимают, что при установившемся движении поток состоит из элементарных струек, которые имеют а) постоянную форму, б) частицы жидкости не переходят из одной струйки в другую. Для характеристики движения жидкости введено понятие линия тока. При установившемся движении линия тока совпадает с траекториями частиц жидкости. Линий тока бесконечное множество. Если вектора скоростей близлежащих линий тока отличаются на малую величину понятие линия тока можно заменить понятием струйка. 4 Живым (нормальным) сечением называется поверхность, проведенная внутри потока перпендикулярно к линиям тока. Живое сечение можно провести ко всему потоку, или к его элементарной струйке. Скорость в любом живом сечении элементарной струйки постоянна (см. понятие элементарная струйка). 5 Расход жидкости Q это величина, равная объему жидкости, протекающей через живое сечение потока в единицу времени Q = 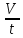 , 1-6)где V – объем жидкости, протекающей через живое сечение потока за время t. [Q] = 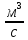 .Если площадь живого сечения S, средняя скорость в живом сечении υ, l –расстояние, пройденное частицей жидкости t, то Q = 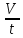=  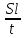= Sυ.При напорном движении поток не должен иметь пустот и разрывов. Так как поток может проходить через разные живые сечения, расход жидкости в каждом живом сечении должен быть постоянным, т.е. Q = S υ = Const 1-7) Выражение 1-7) называется уравнением неразрывности струи. Следствие из уравнения неразрывности: средние скорости потока жидкости обратно пропорциональны площадям своих нормальных сечений. Это положение легко доказать: в сечениях S1 и S2 потока расход одинаков, т.е. Q= S1υ1 = S2υ2, откуда 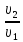 = .6 Мощность потока жидкости. В любом живом сечении действует сила F = pS. Мощность, развиваемая этой силой P = Fυ =pSυ =pQ 1-8) 1.1.4 Уравнение Бернулли Уравнение Бернулли устанавливает связь между скоростью и давлением в отдельных т 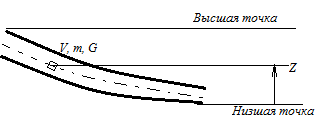 очках потока.В потоке жидкости на уровне Z от низшей точки взята частица в виде элементарного параллелепипеда с объемом V, массойm и весом G = mg. Полная энергия этой частицы состоит из: а) потенциальной энергии положения относительно низшей точки; б) потенциальной энергии давления; в) кинетической энергии частицы. По закону сохранения энергии полная энергия частицы во вс ех точках пространства должна быть постоянной. Потенциальная энергия положения Еz = Gz =mgz. Потенциальную энергию давления можно определить из следующих соображений. Если площадь параллелепипеда объема V, перпендикулярная скорости потока, равна S, а давление в ее плоскости равно р, то силаF,действующая на нее, F= pS. При размере параллелепипеда вдоль потока l, можно выбратьl настолько малым, чтобы давление на протяжении этой длины практически не менялось. Тогда работа по перемещению параллелепипеда объема V, которая может быть произведена за счет давления р, т.е. потенциальная энергия давления Ер = Fl = pSl= pV = p  .Кинетическая энергия выбранного объема массы m Ек =  .Полная энергия частицы Е = Еz + Еp +Еk = Const. mgz + p + = Const. 1-9)Соотношение 1-9) используют, разделив правую и левую части на mg: z + 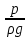 +  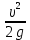= Const 1-10)Выражение 1-10) представляет собой ураввнение Бернулли. Координаты z, p, V выбираются для конкретного живого сечения трубки тока. В другом живом сечении z, p, Vмогут быть другими. Но полная энергия точек разных живых сечений струйки одинакова. Поэтому для двух точек, находящихся в одной струйке тока, z1+  +  .Уравнение Бернулли покаывает, что скорость жидкости в дааой точке зависит от давления в этой точке и наоборот. Особенно хорошо это видно, когда z = 0 (трубка горизонтальна). 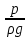+ 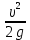= Const.Из этого сотношения хорошо видно, что увеличение скорости ведет к уменьшению давления! Уравнение Бернулли для реальной жидкости. Соотноение 1-10) выведено для идеальной жидкости. Оно не учитывает следующего. 1.Поток состоит не из одной, а из многих струек. Надо брать среднюю υсрскорость в сечении. Обычно так и делают, но слово «ср» не пишут, а подразумевают. 2.Если находить υср =  , то не учитывается распределение скорости струек в потоке. Для слагаемого, содержащего скорость, вводят коэффициент α, учитывающий форму сечения.1< α < 2. 3.В реальном потоке, в отличие от идеального, есть потери. Чтобы их учесть, вводят слагаемоеhП, учитывающий потери давления. Уравнение Бернулли для реальной жидкости выглядит так: z + 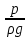+  + hП = Const 1-11)Чтобы выяснить физический смысл коэффициентаhП , надо рассмотреть горизонтальный поток в трубе одинакового сечения со скоростями в сечениях 1 и 2 почти одинаковыми. В этом случае z1 = z2, υ1 = υ2 , α1 = α2 = α. С такими условиями уравнение Бернулли можно записать так: + =  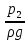+  . - 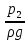= 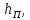откуда видно, что p1 – p2 = ρg ,т.е. характеризует уменьшение давления в трубе, которое поисходит за счет а) трения в трубе, б) за счет преодоления нагрузки (для чего и создана система).1.1.5 Ламинарное и турбулентное течение жидкости. Понятие о кавитации. Гидралический удар. Ламинарное течение характеризуется тем, что жидкость из струек не переходит в соседние. Пульсации скорости потока и давления отсутствуют. При турбулентном режиме могут быть пульсации давления и скорости потока, частицы жидкости перемещаясь, постоянно перемешиваются. Это показал О. Рейнольдс в своих опытах с окрашенными жидкостями. Опытами установлено, что режим течения зависит от средней скорости потока жидкости; особенностей сечения (например, диаметра трубы); кинематической вязкости ν = жидкости.Режим течения определяется числом Рейнольдса (обозначается Re) . Для трубы круглого сечния диаметра dRe =  =  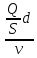=  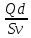= =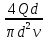  .Чтобы движение было ламинарным, необходимо Re < Reкр. Критическое число Рейнольдса Reкр определяется экспериментально. ЕслиRe ≥ Reкр, поток из ламинарного переходит в турбулентный. Для примера показаны числа Reкр для различных случаев. Гладкие круглые трубы 2300 Гибкие рукава 1600 Щели золотников 260 Щели конических клапанов 80 Для цилиндрических прямых труб число Рейнольдса определяется с помощью соотношения Re = 21200 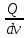 ,где Q—расход жидкости, [Q]  ,d - внутренний диаметр трубы, [d] мм, ν – кинематическая вязкостьжидкости, [ν]  .П 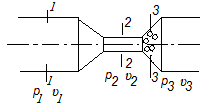 онятие о кавитации.Чем выше давление, тем выше температура кипения жидкости. Если жидкость находилась при высоком давлении, затем давление резко снизилось, жидкость может испаряться в внутри всего объема с образованием пузырьков, заполненных паром этой жидкости. Процесс возникновения пузырьков пара жидкости при снижении давления называется кавитацией. Наблюдать явление кавитации можно с помощью горизонтальной стеклянной трубки, изображенной на рис. Жидкость движется слева-направо. Скорость и давление в сечениях 1-1, 2-2, 3-3 соответствуют показанным на рис. Для сечений 1-1 и 2-2 можно написать уравнение Бернулли: = 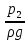+ 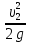. 1-12)Из уравнения неразрывности струи υ1S1 = υ2S2 следует, что υ2> υ1. Тогда в соответствии с 1-12) р2 < p1 . Давление р2 может понизиться настолько, что станет ниже давления парообразования и в жидкости будут возникать пузырьки пара. Это наблюдается в узкой части трубки в виде уменьшения прозрачности жидкости. В зоне 3 скорость падает, давление растет. Газ растворяется в жидкости с большой скоростью. Явление, которое называется схлопываанием, сопровождается вибрацией, шумом, эрозионным разрушением стенок трубки. Кавитация уменьшает производительность насосов, жидкость становится сжимаемой, возникают динамические нагрузки на элементы привода, снижается надежность. Кавитация повышается при растворении в рабочей жидкости воздуха и газов. Для борьбы с кавитацией применяют следующие меры: подпор рабочей жидкости при входе в насос (в зоне 2-2 давление также повысится); уменьшение скорости потока; уменьшение максимальной скорости поршней гидроцилиндров (уменьшениее давления в зоне поршней происходит на меньшую величину). П  онятие о гидравлическом ударе. Теория гидравлического удара была разработана в 1899 году Н.Е. Жуковским. Понять суть явления помогает рисунок, на котором имеется большая емкость, из которой по трубе вытекает жидкость. На конце трубы имеется заслонка, которую можно закрыть достаточно быстро. Жидкость вытекает со средней скоростью по всей трубеυ. Каждая частица жидкости массы m обладает кинетической энергиейE = . При быстром закрытии заслонки вследствие несжимаемости жидкости все частицы останавливаются одновременно. Кинетическая энергия всей массы воды преобразуется в потенциальную энергию давления на заслонку и стенки трубы. Вблизи заслонки давления, возникающие от каждого вертикального объема жидкости, суммируются. Максимальное давление возникает вблизи заслонки. По мере удаления от заслонки давление убывает. Сила воздействия на заслонку может достигать очень больших величин и называется полным гидравлическим ударом.Жидкость упруга. Всплеск давления вблизи заслонки со скоростью, близкой к скорости звука в жидкости (1200…1400  , передается в обратном направлении. Скорость распространения зависит не только от модуля объемного сжатия жидкости, но и от материала трубы, отношения диаметра трубы к толщине стенки.Достигнув резервуара, волна возвращается снова к задвижке, но с потерей полуволны. Это создает зону пониженного давления у заслонки. Кроме того создается большой поток жидкости в резервуар, а затем обратный поток, создающий повторное повышение давления в области заслонки. В отдельных случаях, когда длина трубопровода невелика или заслонка закрывается сравнительно медленно отраженная от резервуара волна успевает достичь заслонки до окончания ее закрытия. Возникает непрямой гидравлический удар. Для предотвращения гидравлического удара используют следующие меры. Увеличение отношения внутреннего диаметра трубы к толщине стенки (  .Увеличение времени закрывания заслонок. Уменьшение скорости жидкости. 4. Уменьшение длины трубопровода. Вэтом случае возникает опасность непрямого гидравлического удара, но он менее опасен, чем прямой. Повышение прочности слабых звеньев. Включение гидроаккумуляторов, служащих для борьбы с всплесками давления. Существуют устройства, преднамеренно использующие гидроудар: гидротараны, гидроимпульсаторы, устройства очистки поверхности и др. 1.1.6 Расчет простых трубопроводов. Под простым понимается трубопровод, не имеющий боковых ответвлений. В расчет трубопровода входит решение следующих задач. -Выбрать условный проход. - Определить потери давления. - Определить толщину стенок. |