Логика. Конспект книги
 Скачать 1.72 Mb.
|
|
Глава VI ЛОГИЧЕСКИЕ ОСНОВЫ ТЕОРИИ АРГУМЕНТАЦИИ § 1. Понятие доказательства Познание отдельных предметов, их свойств начинается с чувственных форм (ощущений и восприятии). Мы видим, что этот дом еще не достроен, ощущаем вкус горького лекарства и т. д. Открываемые этими формами истины не подлежат особому доказательству, они очевидны. Однако во многих случаях, напри мер, на лекции, в сочинении, в научной работе, в докладе, в ход” полемики, на судебных заседаниях, на защите диссертации и во многих других, нам приходится доказывать, обосновывать вы сказываемые нами суждения. Доказательность - важное качество правильного мышления. Доказательство связано с аргументацией, но они не тождественны. Аргументация - способ рассуждения, включающий доказательство и опровержение, в процессе которого создается убеждение в истинности тезиса и ложности антитезиса как у самого доказывающего, так и оппонентов; обосновывается целесообразное принятия тезиса с целью выработки активной жизненной позиции реализации определенных программ действий, вытекающих из доказываемого положения'. Понятие “аргументация” богаче по содержанию, чем понятие “доказательство”: целью доказательства является установление истинности тезиса, а целью аргументации еще и обоснование целесообразности принятия этого тезиса, пою его важного значения в данной жизненной ситуации и т. п. В теории _____________________ 'См.: Брутян Г. А. Аргументация. // Вопросы философии. 1982. №11. 209 аргументации “аргумент” также понимается шире, чем в теории доказательства, ибо в первой имеются в виду не только аргумен ты, подтверждающие истинность тезиса, но и аргументы, обос новывающие целесообразность его принятия, демонстрирующие его преимущества по сравнению с другими подобными утвержде ниями (предложениями). Аргументы в процессе аргументации го раздо разнообразнее, чем в процессе доказательства. Форма аргументации и форма доказательства также не сов падают полностью. Первая, как и последняя, включает в себя различные виды умозаключений (дедуктивные, индуктивные, по аналогии) или их цепь, но, кроме того, сочетая доказательство и опровержение, предусматривает обоснование. Форма аргумента ции чаще всего носит характер диалога, ибо аргументирующий не только доказывает свой тезис, но и опровергает антитезис оппонента, убеждая его и/или являющуюся свидетелем дискус сии аудиторию в правильности своего тезиса, стремится сде лать их своими единомышленниками. Диалог как наиболее аргументированная форма ведения бесе ды пришел к нам из древности (так, Древняя Греция - родина диалогов Платона, техники спора в форме вопросов и ответов Сократа и т. п.). Но диалог - это внешняя форма аргументации: оппонент может только мыслиться (что особенно наглядно про является в письменной аргументации). Внутренняя форма аргу ментации представляет собой цепь доказательств и опроверже ний аргументирующего в процессе доказательства им тезиса и осуществления убеждения'. В процессе аргументации выработка убеждений у собеседника или аудитории часто связана с их пере убеждением. Поэтому в аргументации велика роль риторики в ее традиционном понимании как искусства красноречия. В этом смы сле до сих пор представляет интерес “Риторика” Аристотеля, в которой наука о красноречии рассматривается как теория и прак тика убеждения в процессе доказательства истинности тезиса. “Слово есть великий властелин, который, обладая весьма малым и совершенно незаметным телом, совершает чудеснейшие дела. Ибо оно может и страх изгнать, и печаль уничтожить, и радость вселить и сострадание пробудить”, - писал древнегреческий _____________________ 'См.: БрутянГ.А. Аргументация. Ереван, 1984. 210 ученый Горгий об искусстве аргументации'. Не было периода в истории, когда бы люди не аргументировали. Без аргументации высказываний невозможно интеллектуальное общение, ибо она -необходимый инструмент познания истины. Теория доказательства и опровержения является в современных условиях средством формирования научно обоснованных убеждений. В науке ученым приходится доказывать самые раз личные суждения, например, суждения о том, что существовало до нашей эры, к какому периоду относятся предметы, обнаруженные при археологических раскопках, об атмосфере планет Солнечной системы, о звездах и галактиках Вселенной, теоремы математики, суждения о направлениях развития электронной техники, о возможности долгосрочных прогнозов погоды, ( тайнах Мирового океана и космоса. Все эти суждения должны быть научно обоснованы. Доказательство - это совокупность логических приемов обо снования истинности тезиса. Доказательство связано с убеждением, но не тождественно ему: доказательства должны основываться на данных науки и общественно-исторической практики, убеждения же могут быть основаны, например, на религиозной вере, на предрассудках, на неосведомленности людей вопросах экономики и политики, на видимости доказательности, основанной на различного рода софизмах. Поэтому убедить еще не значит доказать. Структура доказательства: тезис, аргументы, демонстрация Тезис - это суждение, истинность которого надо доказать. Аргументы - это те истинные суждения, которыми пользуются при доказательстве тезиса. Формой доказательства, ил демонстрацией, называется способ логической связи между тезисом и аргументами. Приведем пример доказательства. Поль С. Брэгг высказал такой тезис: “Купить здоровье нельзя, его можно только заработать своими собственными постоянными усилиями”. Этот тезис он обосновывает так: “Только упорная и настойчивая работа ________________________ 'См.: МаковельскийА. О. Софисты. Баку, 1940. Вып. 1. С. 36-37. 211 над собой позволит каждому сделать себя энергичным долго жителем, наслаждающимся бесконечным здоровьем. Я сам за работал здоровье своей жизнью. Я здоров 365 дней в году, у меня не бывает никаких болей, усталости, дряхлости тела. И вы можете добиться таких же результатов!”' Виды аргументов Различают несколько видов аргументов: 1. Удостоверенные единичные факты. К такого рода аргументам относится так называемый фактический материал, т. е. статистические данные о населении, территории государ ства, выполнении плана, количестве вооружения, свидетельские показания, подписи на документах, научные данные, научные факты. Роль фактов в обосновании выдвинутых положений, в том числе научных, велика. В “Письме к молодежи” И. П. Павлов призывал молодых ученых к изучению и накоплению фактов: “Изучайте, сопостав ляйте, накопляйте факты. Как ни совершенно крыло птицы, оно никогда не смогло бы поднять ее ввысь, не опираясь на воздух. Факты - воздух ученого. Без них вы никогда не сможете взле теть. Без них ваши “теории” - пустые потуги. Но изучая, экспериментируя, наблюдая, старайтесь не оста ваться у поверхности фактов. Не превращайтесь в архивариу сов фактов. Пытайтесь проникнуть в тайну их возникновения. Настойчиво ищите законы, ими управляющие”2. Ценой десятков тысяч проведенных опытов, сбора научных фактов И. В. Мичурин создал стройную систему выведения но вых сортов растений. Сначала он увлекся работами по акклима тизации изнеженных южных и западноевропейских плодовых куль тур в условиях средней полосы России. Путем гибридизации он ________________________ 'Брэгг П. С. Чудо голодания. М., 1989. С. 6. Он умер в декабре 1976 г. в возрасте 95 лет. Во время катания на доске у побережья Флориды его накрыла гигантская волна. Его оплакивали 5 детей, 12 внуков, 14 правнуков и тысячи последователей. 2Павлов И. П. Избранное произведения. М., 1951. С. 51-52. 212 сумел создать свыше 300 сортов плодовых и ягодных культур. Это яркий пример того, как подлинный ученый собирает и обра батывает огромный научный фактический материал. 2. Определения как аргументы доказательства. Опре деления понятий обычно даются в каждой науке. Правила опре деления и виды определений понятий были рассмотрены в теме “Понятие”, и там же были приведены многочисленные примеры определений понятий различных наук: математики, химии, био логии, географии и пр. 3. Аксиомы. В математике, механике, теоретической физи ке, математической логике и других науках, кроме определений вводят аксиомы. Аксиомы - это суждения, которые принима ются в качестве аргументов без доказательства. 4. Ранее доказанные законы науки и теоремы как ар гументы доказательства. В качестве аргументов доказательства могут выступать ранее доказанные законы физики, химии биологии и других наук, теоремы математики (как классической, так и конструктивной). Юридические законы являются аргументами в ходе судебного доказательства. В ходе доказательства какого-либо тезиса может использоваться не один, а несколько из перечисленных видов аргументов. § 2. Прямое и непрямое (косвенное) доказательства Доказательства по форме делятся на прямые и непрямые (косвенные). Прямое доказательство идет от рассмотрения аргументов к доказательству тезиса, т. е. истинность тезиса непосредственно обосновывается аргументами. Схема этого доказательства такая: из данных аргументов (а, b, с, ...) необходимо следует доказываемый тезис q. По этому типу проводятся доказательства в судебной практике, в науке, в полемике, в сочи нениях школьников, при изложении материала учителем и т. д. Широко используется прямое доказательство в статистических отчетах, в различного рода документах, в постановлениях, в художественной и другой литературе. Приведем пример прямого доказательства, использованного И. А. Буниным в стихе творении “В степи”: 213 А к нам идет угрюмая зима: Засохла степь, лес глохнет и желтеет, Осенний ветер, тучи нагоняя, Открыл в кустах звериные лазы, Листвой засыпал долы и овраги, И по ночам в их черной темноте, Под шум деревьев, свечками мерцают, Таинственно блуждая, волчьи очи... Да, край родной не радует теперь! Чтобы обосновать тезис: “Труд доктора - действительно са мый производительный труд”, Н. Г. Чернышевский использует прямое доказательство с помощью таких аргументов: предохраняя или восстанавливая здоровье, доктор приобретает об ществу все те силы, которые погибли бы без его забот. Учитель на уроке при прямом доказательстве тезиса “Народ -творец истории”, показывает; во-первых, что народ является соз дателем материальных благ, во-вторых, обосновывает огромную роль народных масс в политике, разъясняет, как в современную эпоху народ ведет активную борьбу за мир и демократию, в-треть их, раскрывает его большую роль в создании духовной культуры. На уроках химии прямое доказательство о горючести сахара может быть представлено в форме категорического силлогизма: Все углеводы - горючи. Сахар - углевод. Сахар горюч. В современном журнале мод “Бурда” тезис “Зависть - ко рень всех зол” обосновывается с помощью прямого доказатель ства следующими аргументами: “Зависть не только отравляет людям повседневную жизнь, но может привести и к более серь езным последствиям, поэтому наряду с ревностью, злобой и ненавистью, несомненно, относится к самым плохим чертам характера. Подкравшись незаметно, зависть ранит больно и глубоко. Че ловек завидует благополучию других, мучается от сознания того, что кому-то более повезло”'. _____________________ 'Журнал “Бурда”. М., 1989. № 1. С. 2. 214 Непрямое (косвенное) доказательство - это доказательство, в котором истинность выдвинутого тезиса обосновывается путем доказательства ложности антитезиса. Если тезис об значить буквой а, то его отрицание (  ) будет антитезисом, т.е. противоречащим тезису суждением.Апагогическое косвенное доказательство (или доказательство “от противного”) осуществляется путем ycтановления ложности противоречащего тезису суждения. Этот метод часто используется в математике. Пусть а -тезис или теорема, которую надо доказать. Предполагаем от противного, что а ложно, т. е. истинно не-а (или ). Из допущения  выводим следствия, которые противоречат действительности или ранее доказанным теоремам. Имеем а , при этом - ложно, значит, истинно его отрицание, т.е.  , которое по закону двузначной классической логики (→а) дает а. Значит, истинно а, что и требовалось доказать.Следует заметить, что в конструктивной логике формула →а не является выводимой, поэтому в этой логике и в конструктивной математике ею пользоваться в доказательствах нельзя. Закон исключенного третьего здесь также “отвергается” является выводимой формулой), поэтому косвенные доказательства здесь не применяются. Примеров доказательства “от противного” очень много в школьном курсе математики. Так, пример, доказывается теорема о том, что из точки, лежащей вне прямой, на эту прямую можно опустить лишь один перпендикуляр. Методом “от противного” доказывается и следующая теорема: “Если две прямые перпендикулярны к одной и той же плоскости, то они параллельны”. Доказательство этой теоремы пpямо начинается словами: “Предположим противное, т. е. что прямые АВ и CD не параллельны”.Разделительное доказательство (методом исключения). Антитезис является одним из членов разделительного суждения, в котором должны быть обязательно перечислены все возможные альтернативы, например: Преступление мог совершить либо А, либо В, либо С. Доказано, что не совершали преступление ни А, ни В. Преступление совершил С. 215 Истинность тезиса устанавливается путем последователь ного доказательства ложности всех членов разделительного су ждения, кроме одного. Здесь применяется структура отрицающе-утверждающего модуса разделительно-категорического силлогизма. Заключе ние будет истинным, если в разделительном суждении преду смотрены все возможные случаи (альтернативы), т. е. если оно является закрытым (полным) дизъюнктивным суждением: a  b c d; ^  ^  ^  d Как отмечалось ранее, в этом модусе союз “или” может употребляться и как строгая дизъюнкция (\/ ), и как нестрогая дизъюнкция (ύ), поэтому ему отвечает также схема: a ύ b ύ c ύ d; ^ ^ ^ —————-----------------------------------------------------————— d § 3. Понятие опровержения Опровержение - логическая операция установления ложно сти или необоснованности ранее выдвинутого тезиса. Опровержение должно показать, что: 1) неправильно постро ено само доказательство (аргументы или демонстрация); 2) вы двинутый тезис ложен или не доказан. Суждение, которое надо опровергнуть, называется тезисом опровержения. Суждения, с помощью которых опровергается тезис, называются аргументами опровержения, Существуют три способа опровержения: I) опровержение те зиса (прямое и косвенное); II) критика аргументов; III) выявле ние несостоятельности демонстрации. 1. Опровержение тезиса (прямое и косвенное) Опровержение тезиса осуществляется с помощью следую щих трех способов (первый - прямой способ, второй и третий -косвенные способы). 1. Опровержение фактами - самый верный и успешный способ опровержения. Ранее говорилось о роли подбора фактов, 216 о методике оперирования ими; все это должно учитываться в процессе опровержения фактами, противоречащими тезису. Должны быть приведены действительные события, явления, статистические данные, которые противоречат тезису, т. опровергаемому суждению. Например, чтобы опровергну тезис “На Венере возможна органическая жизнь”, достаточно привести такие данные: температура на поверхности Венеры 470-480° С, а давление - 95-97 атмосфер. Эти данные свидетельствуют о том, что жизнь на Венере невозможна 2. Устанавливается ложность (или противоречивость) следствий, вытекающих из тезиса. Доказывается, что из данного тезиса вытекают следствия, противоречащие истине. Этот прием называется “сведение к абсурду” (reductioadabsurdum). Поступают так: опровергаемый тезис временно признается истинным, но затем из него выводятся такие следствия, которые противоречат истине. В классической двузначной логике (как уже отмечалось) метод “сведения к абсурду” выражается в виде формулы: =a→F,Df где F- противоречие или ложь. В более общей форме принцип “сведения (приведения) к абсурду” выражается такой формулой: (а → b) → ((а → ) →3. Опровержение тезиса через доказательство антитезиса. По отношению к опровергаемому тезису (суждению а ) выдвигается противоречащее ему суждение (т. е. не-а), и суждение не-а (антитезис) доказывается. Если антитезис истинен, то тезис ложен, и третьего не дано по закону исключенного третьего. Например, надо опровергнуть широко распространенный тезис: “Все собаки лают” (суждение А, общеутвердительное). Для суждения А противоречащим будет суждение О - частноотрицательное: “Некоторые собаки не лают”. Для доказательства последнего достаточно привести несколько примеров или хотя бы одинпример: “Собаки у пигмеев никогда не лают”'. Итак, доказано ____________________ 'По материкам и странам. М., 1981. С. 79. 217 суждение О. В силу закона исключенного третьего, если О -истинно, то А - ложно. Следовательно, тезис опровергнут. II. Критика аргументов Подвергаются критике аргументы, которые были выдвину ты оппонентом в обоснование его тезиса. Доказывается лож ность или несостоятельность этих аргументов. Ложность аргументов не означает ложности тезиса: тезис мо жет оставаться истинным: а→b, ——————————— Вероятно, 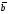Нельзя достоверно умозаключать от отрицания основания к отрицанию следствия. Но бывает достаточно показать, что те зис не доказан. Иногда бывает, что тезис истинен, но человек не может подобрать для его доказательства истинные аргументы. Случается и так, что человек не виновен, но не имеет достато чных аргументов для доказательства этого. В ходе опроверже ния аргументов следует об этих случаях помнить. III. Выявление несостоятельности демонстрации Этот способ опровержения состоит в том, что показываются ошибки в форме доказательства. Наиболее распространенной ошибкой является та, что истинность опровергаемого тезиса не вытекает, не следует из аргументов, приведенных в подтвержде ние тезиса. Доказательство может быть неправильно построен ным, если нарушено какое-либо правило дедуктивного умозак лючения или сделано “поспешное обобщение”, т. е. неправильное умозаключение от истинности суждения I к истинности сужде ния А (аналогично, от истинности суждения О к истинности суж дения Е). Но обнаружив ошибки в ходе демонстрации, мы опровергаем ее ход, но не опровергаем сам тезис. Задача же доказательства истинности тезиса лежит на том, кто его выдвинул. Часто все перечисленные способы опровержения тезиса, аргументов, хода доказательства применяются не изолирован но, а в сочетании друг с другом. 218 |