Матрицы. Конспект лекций, читаемых в курсе Высшая математика

• Название: Конспект лекций, читаемых в курсе Высшая математика
• Дата: 17.12.2020
• Размер: 95.27 Kb.
• Имя файла: Матрицы.docx
• Тип: Конспект; #161551
• страница: 13 из 13

   

_ 3 0 3 _{ } 5 8 1 _{ } 25 35 45_

б) ^{A   7 1 3 } , ^{B   3 4 5 } , ^{C   31 21 19 } .

 

 
^ 2 3 6 ^

 

 
^ 6 2 0 ^

 

 
^ 5 10 37 ^

22. 
    Вычислить значение матричного выражения:
    

а) ( AB)¹⁰ , если

_ 1 0 _

A ,

B  ^

1 0 _

,

 

 
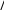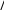
^ 1 2^{ }1 2 1 2 ^

б) ( AB)¹⁵ , если

_ 3 5 1 _

^{A   1 6 2 } ,

_ 2 5

B  ^ 1 5

1_

^{2 } ;

   

^ 1 3 2 ^{ } 1 3 1^

в) ( AB)⁵ , если

 

_ 3 9 10 _

 
^{A   1 6 2 } ,


 
^ 1 0 5 ^

 

_ 2 9 10 _

 
^{B  11 11 13}.


 
^ 1 0 4 ^

22. 
    Вычислить степень матрицы:
    


A  ^{ 2}

3

^1⁶

2^{ ,}

 ^{0 0 1} ³

 
B  ^ 0 1 0 ^

 
^{  } 1 0 0 ^

22. 
    Какие матрицы называются перестановочными?
    
23. 
    Какие виды матриц перестановочны всегда, если их произведение существует?
    
24. 
    Найти все матрицы, перестановочные с матрицей:
    

_ 1 1 _

_ 0 0 1 <sub>

</sub> 1 0 0 _

а) _{ } , б) ^{ 0 1 0 } , с) ^{ 0 1 0 } .

_ 1 1_

 

 
^ 1 0 0 ^

 

 
^ 0 0 1 ^

22. 
    Что называется многочленом от матрицы?
    
23. 
    Вычислить значение многочлена от матрицы:
    

а) f(t)  3  4t; A= <sup> 1

2</sup> _;

4 0
 

 

 ^{2 0 4} 


 
б) f(t)  3  4t 2t²; A= ^ 1 2 3 ^.

^ 0 4 3^

 

22. 
    Два различных по качеству вида обуви продаются в трех магазинах. Матрица ^A — объемы продаж этих товаров в магазинах в 1-м квартале, матрица ^B — во 2-м квартале.
    

Определить: 1) объем продаж за два квартала; 2) прирост продаж во 2-м квартале по сравнению с первым:

_ 3 3 _{ } 4 4 _

^{A   6 3 ; B   6 4 } .

   


4 4 2 5
   

   

22. 
    Предприятие производит три типа продукции, используя два вида ресурсов. Норма ^{затрат ресурсов} i ^{-го вида на производство продукции j -ого задана матрицей затрат A ,} выпуск продукции за квартал — матрицей B , стоимость единицы каждого вида ресурсов задана матрицей ^C . Найти матрицу полных затрат ресурсов каждого вида и полную стоимость всех затраченных ресурсов, если:
    

^ 2 1 4^{
A   3 2 1  ; B} ^{15 25 20}^{T ; C} ^{6 3} ^.

 

22. 
    При каком условии для матриц ^A и ^B выполняется равенство: а) ( A  B)²  A²  2AB  B² ;
    

б) A²  B²  ( A  B)( A  B) , если произведения AB и BA определены.

22. 
    Что такое симметричная матрица?
    

Привести пример симметричной матрицы 4-го порядка.

22. 
    Показать, что след матрицы обладает следующими свойствами: а) tr( A B)  trA trB;
    

б) tr(A)  trA;

в) ^{trAT  trA;}

г) tr( AB)  tr(BA).

22. 
    Доказать, что матрица
    

^AT ^Aквадратная и симметричная для любой матрицы ^A.

22. 
    Дана система ^m уравнений с ⁿнеизвестными
    

 ^{a11x1  a12 x2  a1n xn  b1}






(*)


^a_m1x₁  a_m2 x₂  a_mn x_n  b_m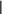

Доказать, что запись системы в форме (*) и в форме

Ax  b,

где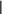

A  a_ij

, x  (x₁, x_n )^T,b  (b₁,b_m )^T, есть одно и то же.

22. 
    Даны матрицы:
    

^{A 2 3 5; X }  ^{x x x}
^{T ; b} ^{0 5} ^.

^ 6 4 0^

1 2 3

 

Записать соответствующую систему уравнений в форме (*).

22. 
    Дать определение обратной матрицы.
    
23. 
    Чем обратимая матрица отличается от обратной?
    
24. 
    Перечислить свойства обратимых матриц.
    
25. 
    Какие преобразования матриц называются элементарными?
    

22. 
    С помощью элементарных преобразований привести матрицы из примера к треугольному виду.
    
23. 
    Дать определение приведенной матрицы.
    
24. 
    Какие из ниже перечисленных матриц являются приведенными?
    

_ 3 2 4 1 _

_ 0 0 0 1 <sub>

</sub> 0 0 4 _

A  ^ 5 0 0 1 ^ ,

^B ^{0 0 0 0} ^{, C   0 0 1 0  ,}

_ 1 0_

D  ^,

F  ^ 0 0 0 ^ .

   

 _{0 1}  _{ }

^ 6 1 0 2 <sup>

</sup> 0 1 0 0 <sup>

  </sup> 3 0 0 ^

     

22. 
    Что такое ранг матрицы?
    
23. 
    Вычислить ранг матриц из примера 42.
    
24. 
    В чѐм сходство и отличие операций над матрицами и числами?
    
25. 
    Деревообрабатывающая фабрика из двух сортов древесины производит фанеру
    

и брусы. На 100 кв.м. фанеры нужно 2 куб.м еловой и 6 куб.м. пихтовой древесины и прибыль равна 1700 руб. На 100 погонных метров елового бруса нужно 5 куб.м., а на 100 погонных метров пихтового бруса нужно 4 куб.м. древесины, прибыль же равна соответственно 800

и 1000 руб. Сколько видов продукции производит цех? Сколько видов ресурсов используется? Составьте матрицу норм расхода, векторы удельной прибыли и запасов ресурсов. Докажите, что фанеру производить невыгодно, и найдите план, дающий максимальную прибыль.

22. 
    Пусть _E — единичная матрица. Проверьте, что если произведение ^{XE(EX )}
    

существует, то

XE  X (EX

^{ X )} , какова бы ни была матрица X .

22. 
    Для пространства ^R3
    

напишите матрицу, которая: а) умножает первую

компоненту вектора на 3, вторую — на 2, третью оставляет неизменной; б) делает третью компоненту суммой всех трех исходных компонент; вторую компоненту делает суммой 1-й и 2-й, а 1-ю компоненту оставляет неизменной.

22. 
    Убедитесь на конкретных примерах, что если Y — неотрицательная вектор строка,
    

A — матрица,

X , B ^{— векторы — столбцы, то неравенство AX  B сохранится при}

умножении его слева на Y . Вспомните правила действий с обычными неравенствами.