Матрицы. Конспект лекций, читаемых в курсе Высшая математика

• Название: Конспект лекций, читаемых в курсе Высшая математика
• Дата: 17.12.2020
• Размер: 95.27 Kb.
• Имя файла: Матрицы.docx
• Тип: Конспект; #161551
• страница: 5 из 13

§ 1.13 Технологическая матрица

Пусть предприятие, используя m видов ресурсов, производит n видов изделий. На производство одного изделия j -го вида тратится a_ij единиц ресурса i -го вида, т.е. a_ij —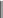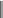

число единиц i -го вида сырья для производства одной единицы j -го вида изделий (норма

расхода i -го сырья на производство j -го вида изделий). Матрица A 

расхода (технологическая матрица)

^aij

— матрица норм

изделие сырье	П1	П2		Пj		Пn
P1	a11	a12		a1j		a1n
P2	a21	a22		a2 j		a2n
Pi	ai1	ai2		aij		ain
Pm	am1	am2		amj		amn

m

^Сумма _ a_ij ^{есть расход всех видов ресурсов на производство одной единицы}

i1

продукции j -го вида (реализуется технологический процесс производства j -го вида

n

изделий). Сумма

_ ^a_ij — расход i -го ресурса на единицу каждого продукта (единичная

j1

интенсивность каждой технологии).

Введѐм в рассмотрение план производства продукции всех видов, задаваемый

вектором

x  (x₁, x₂ ,..., x_n )^T. Естественно считать x  0 . Для реализации этого плана

потребуется

n



j1

a_{1 j} x _j ^{единиц ресурса 1-го вида,}

n



j1

^a2 j^xj

единиц ресурса 2-го вида,


n

j1

^aij^x j

единиц ресурса i -го вида. Указанные суммы есть компоненты вектора-столбца,

представляющего собой произведение матрицы A на вектор плана x.

Введѐм в рассмотрение ещѐ и вектор удельной прибыли

p  ( p₁, p₂ ,..., p_n ) , где p _j –

удельная прибыль от реализации единицы продукции j -го вида. Тогда скалярное произведение ( p, x) представляет собой величину прибыли, полученной от реализации всей продукции.

Пусть вектор

b  (b₁, b₂ ,..., b_m )^T– вектор запасов всех видов ресурсов, имеющихся на

складе. Тогда очевидно, что матричное неравенство A  x  b означает реальность реализации плана производства x при имеющихся запасах b и использовании технологий A . И здесь приходим к одной из основных задач экономического планирования — задаче оптимального планирования:

из всех возможных планов производства найти такой, который бы при наличии определѐнных запасах ресурсов приносил бы максимальную прибыль, т.е.

( p, x)  max,

Ax b, .

x  0
Пример 15. Завод производит электродвигатели двух видов. На один электродвигатель первого вида нужно 5 кг. металла и 3 кг. проволоки, второго вида — 3 кг. металла и 2 кг. проволоки. От реализации одного электродвигателя завод получает прибыль 600 и 500 руб. соответственно. Завод располагает 4,8 т. металла и 3 т. проволоки. Сколько видов продукции производит завод? Сколько видов ресурсов используется? Составьте матрицу норм расхода, векторы удельной прибыли и запасов ресурсов. Рассмотрите несколько планов производства