Матрицы. Конспект лекций, читаемых в курсе Высшая математика
 Скачать 95.27 Kb. Скачать 95.27 Kb.
|
|
Введение Настоящее учебное пособие представляет собой конспект лекций, читаемых в курсе «Высшая математика» студентам экономических специальностей Южного федерального университета и предназначено в качестве материала для самостоятельной работы. Эта первая часть курса охватывает вопросы линейной алгебры. Также здесь приводятся задачи и вопросы для самостоятельного решения. Глава 1. Матрицы и операции над ними § 1.1 Основные определенияОпределение. Матрицейразмера mn называется прямоугольная таблица чисел a11 a 21 a12 a22 a1n a 2n (1) m1 m2 mn a a a   Матрицы будем обозначать заглавными латинскими буквами, их элементы — Матрицы будем обозначать заглавными латинскими буквами, их элементы —соответствующими прописными буквами с индексами: A aij . Первый индекс элемента матрицы означает номер строки, в которой находится элемент, второй — номер столбца. Определение. Векторами назовем матрицы, состоящие из одной строки или одного столбца. З а м е ч а н и е . Понятие «вектор» в математике многозначно. В геометрии мы определяли вектор как направленный отрезок прямой. Понятие «вектор» может обозначать и упорядоченный набор некоторых объектов, а не только чисел. Определение. Матрицы, у которых число строк и столбцов совпадают, называются квадратными. Элементы a11, а22 ,, акк образуют главную диагональ матрицы, аих сумма называется следом матрицы (обозначают trA ). Определение. Квадратная матрица, у которой на главной диагонали стоят единицы, а все остальные элементы суть нули, называется единичнойматрицей. Определение. Квадратная матрица, у которой все элементы выше (ниже) главной диагонали равны нулю, называется нижне(верхне)-треугольной (или просто треугольной). Определение. Матрица, являющаяся одновременно нижне- и верхне-треугольной называется диагональной. Определение. Матрица, все элементы которой нули, называется нулевой и обозначается O . Ниже мы будем рассматривать матрицы, элементами которых являются действительные числа. Множество всех матриц размера m n обозначим Mmn . Для множества квадратных матриц размера n n примем обозначение Mn , и будем говорить, что рассматриваем матрицы порядка n. Множество всех векторов — столбцов длины m обозначим Rm. Пример 1. Матрицы 34 A 1 7 8 3 2 1 , 1 2 В 2 5 3 6 являются матрицами размера являются функции: 2 4 и 3 2 соответственно. Элементами матриц C и D x2 3x 1 ln x 2 sin 3xex2 C 1 x x6 , D tgx cos x 1 en 2esin x . 2 arccos 2x 2 ln cos x 2x x 1 3 0 0 Матрица 1 4 0 5 2 0 является нижне-треугольной матрицей. 1 0 0 0 0 Матрица 0 1 0 0 0 0 1 0 0 0 1 3 0 является единичной порядка 4. Матрица 0 7 3 является диагональной матрицей второго порядка. 1 Матрицы (1,2,3,4,5) и 2 4 являются соответственно вектором-строкой и вектором-столбцом. § 1.2 Равенство матрицОпределение. Две матрицы AиB называются равными, если они одинакового размера и соответствующие элементы обеих матриц равны. Пример 2. Выяснить, какие из следующих матриц равны: 1 A 2 1 , 0 B 0 2 1 , C 1 1 2 1 0 ,  sin(2) cos 1 1 1 sin(2) cos 1 1 1D , F , 2 cos 2 sin 2 2 0 2 cos 2 H sin 3 2 .  2 sin 2 cos 2 Р е ш е н и е .Сравнивать между собой можно лишь матрицы A , B , D , H , т.к. они одинакового размера, а соответственные элементы равны лишь у матриц A и D . Следовательно, равные лишь A и D . § 1.3 Транспонирование матрицОпределение. Пусть матрица A имеет вид (1). Тогда матрица a11 a T 12 a21 a22 am1 a m2 A 1n 2n mn a a a называется транспонированной к матрице A . При транспонировании строки и столбцы матрицы меняются местами. Пример 3. Пусть 2 3 4 5 1 1 4 A 6 7 8 9 , B 2 3 1 2, C , D . 4 4 1 1 4 2 3 Транспонированными к ним будут матрицы 2 6 1 3 7 2 2 3 T T T1 4 A , B , C 1 4 , D . 4 8 3 5 9 4 1 2 4 1 Свойства операции транспонирования.Если A Mmn , то AT M nm . ( AT)T A. Д о к а з а т е л ь с т в о этих свойств очевидно. Определение. Если AT A , то матрица A называется симметричной. Из свойства 1) следует, что симметричные матрицы всегда квадратные (матрица D в примере 3). § 1.4 Сложение матрицОперация сложения определена для матриц одного размера. Пусть A, B Mmn : a11 a 21 a12 a22 a1n a 2n b11 b 21 b12 b22 b1n b 2n A , B . m1 m2 mn m1 m2 mn a a a b b b Суммой матриц A и B называется матрица a11 b11 a12 b12 a1n b1n a b a b 21 21 a22 b22 2n 2n A B . m1 m1 m2 m2 mn mn a b a b a b Пример 4. Сложим две матрицы A 0 1 5 и B 6 3 0 . 4 2 3 1 4 2 C A B 0 6 1 3 5 0 6 2 5 . 4 1 2 4 3 2 5 6 1 В результате получили матрицу C того же размера. Свойства операции сложения матрицОперация сложения матриц коммутативна и ассоциативна, т.е. A B B A — коммутативность. ( A B) C A (B C) — ассоциативность. Д о к а з а т е л ь с т в о следует из соответствующих свойств действительных чисел. A O O A . Здесь O — матрица того же размера, что и матрица A. Для любой матрицы A существует единственная матрица B такая, что A B O. Определение. МатрицаB называется противоположной матрице A и обозначается — A , если A B О . С помощью противоположной матрицы вводится понятие вычитания матриц, а именно A B A (B) . Д о к а з а т е л ь с т в о A Aaij , B  bij bij; AT   aji aji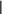 , BT , BT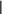 bji bji; A B 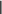 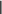 aij bij ; aij bij ;    ( A B)T ( A B)Taji bji AT BT. § 1.5 Умножение матрицы на числоОпределение. Произведением матрицы A вида (1) на число называется матрица a11 a 21 a12 a22 a1n a 2n A . m1 m2 mn a a a Пример 5. Умножим матрицу A на действительное число . 2 3 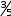 A 1 4 , . A 1 4 , . 12 5 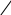 35 (2) 35 (2)35 3 65 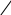 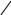     B A B A 35 1 35 4 12 5 .   35 12 35 1235 5 365 3   Свойства операции умножения матрицы на число1) 1 A A, 2) (A) () A, 3) ( ) A A A, 4) ( A B) A B, 5) (A)T AT. Даны две матрицы A и B : |
