ТОК Лекции. Конспект лекций Самара Самарский государственный технический университет 2011
 Скачать 6.93 Mb. Скачать 6.93 Mb.
|
|
Пятиразрядный код с двумя единицами и пример семиразрядного кода с тремя единицами
Правильность принятых кодовых комбинаций в кодах определяется путем подсчета количества единиц, и если, например, в коде С52приняты не две единицы, а в коде С73 – не три единицы, то в передаче произошла ошибка. Код С73может обнаружить все одиночные ошибки, так как при этом в комбинации будет либо две единицы, либо четыре. Кроме того, он позволяет обнаружить часть многократных ошибок (двойные, тройные и т.п.), за исключением случаев, когда одна из единиц переходит в нуль, а один из нулей – в единицу (такое двойное искажение называется смещением). При смещениях искажение также не обнаруживается. Все сказанное справедливо и для кода С52. 4.6.1.2. Распределительный код Распределительным называется код Cn1 с одной единицей в кодовой комбинации.Это разновидность кода с постоянным весом, равным единице. В любой кодовой комбинации длиной п содержится только одна единица. Число кодовых комбинаций в распределительном коде N=Cnl=n. Кодовые комбинации при n=6 можно записать в виде 000001, 000010, 000100, 001000, 010000, 100000. Сложение по модулю 2двух комбинаций показывает, что они отличаются друг от друга на кодовое расстояние d= 2. 4.6.2. Коды, построенные добавлением контрольных разрядов Для построения этих кодов также используется двоичный код на все сочетания. Он образует информационную часть полной кодовой комбинации корректирующего кода, к которой добавляются контрольные разряды, формируемые по определённому правилу. 4.6.2.1. Код с проверкой на чётность Такой код образуется путем добавления к передаваемой комбинации, состоящей из k информационных символов неизбыточного кода, одного контрольного символа т (0 или 1) так, чтобы общее число единиц в передаваемой комбинации было чётным. Таким образом, общее число символов в передаваемой комбинации n = k + 1, так как т=1. Примеры построения кода с проверкой на чётность приведены в табл. 4.10. В приведённых примерах длина исходной кодовой комбинации k=5, это позволяет передать N=25=32 кодовые комбинации. Хотя приписывание контрольного символа и увеличивает разрядность кода до n=6, число комбинаций корректирующего кода остается прежним. Поэтому общее число информационных комбинаций N = 2n-1. Таблица 4.10 Примеры построения кода с проверкой на чётность
Таким образом, этот код обладает избыточностью, так как вместо N=26=64 комбинаций можно применять только N=26-1=32 комбинации. Мера избыточности определяется отношением числа контрольных символов т к длине слова: И=(n – k)/n=m/n. Для пятиразрядного кода с проверкой на чётность избыточность И =1/6. Очевидно, чем длиннее кодовая комбинация, тем меньше избыточность и больше экономичность кода. Добавление контрольного символа увеличивает кодовое расстояние в передаваемых комбинациях от dmin= 1 до dmin = 2. Декодирование кода заключается в том, что на приёмной стороне производят так называемую проверку на чётность. В принятых комбинациях подсчитывают количество единиц: если оно чётное, считают, что искажений не было. Тогда последний контрольный символ отбрасывают и записывают информационную комбинацию. Очевидно, чётное число искажений такой код обнаружить не может, так как число единиц при этом снова будет чётным. В то же время этот код способен обнаружить не только одиночные, но и тройные, пятерные и т.п. ошибки, т.е. любое возможное нечётное число ошибок, так как сумма единиц в принятой кодовой комбинации становится нечётной. В случае если велика вероятность появления многократных ошибок, код использовать нецелесообразно. По изложенному принципу строится код с проверкой на нечётность, который также широко применяется в телемеханике. 4.6.2.2. Код с числом единиц, кратным трём Этот код образуется добавлением к kинформационным символам двух дополнительных контрольных символов (m=2), имеющих такие значения, чтобы сумма единиц, посылаемых в линию кодовых комбинаций, была кратной трем. Примеры комбинации такого кода представлены в табл. 4.11. Таблица 4.11 Примеры кода с числом единиц, кратным трём
Код позволяет обнаружить все одиночные ошибки и любое чётное количество ошибок одного типа, например, только переход нулей в единицы. Не обнаруживаются двойные ошибки разных типов, называемые смещениями, когда один символ переходит из 1 в 0 и одновременно другой символ переходит из 0 в 1. Не обнаруживаются также ошибки одного типа, кратные трем. Декодирование кода заключается в том, что на приёмной стороне полученную комбинацию проверяют на кратность трём единицам. При наличии такой кратности считают, что ошибок не было, два контрольных символа отбрасывают и записывают исходную информационную комбинацию. 4.6.2.3. Код с удвоением элементов (корреляционный код) Помехоустойчивость кода может быть повышена путем установления определенных зависимостей между элементами кодовых комбинаций. Примером такого кода является код с удвоением элементов или корреляционный код, который строится следующим образом. Дл построения кода используется информационная часть в форме двоичного кода. Каждый элемент двоичного кода заменяется двумя символами, причем 1 преобразуется в 10, а 0 – в 01. Таким образом, двоичный код, например, 1010011 преобразуется в кодовую комбинацию корреляционного кода 10011001011010. Корреляционный код содержит вдвое больше элементов, чем исходный. При декодировании ошибка обнаруживается в том случае, если в парных элементах содержатся одинаковые символы, т.е. 11 или 00 (вместо 10 и 01). При отсутствии искажений вторые (чётные) элементы отбрасываются, и остается информационная комбинация. Код обладает высокой помехоустойчивостью, так как ошибка не обнаруживается лишь тогда, когда два рядом стоящих различных символа, соответствующих одному элементу информационной кодовой комбинации, будут искажены так, что 1 перейдет в 0, а 0 – в 1, что маловероятно. Недостатком кода является большая избыточность. 4.6.2.4. Инверсный код В этом коде для увеличения помехоустойчивости к исходной k-разрядной комбинации по определенному правилу добавляется еще kконтрольных разрядов по определённому правилу. В результате в полной кодовой комбинации получается удвоенное число символов. Правило образования кода следующее: если в исходной информационной комбинации содержится чётное число единиц, то добавляемые контрольные разряды повторяют исходную комбинацию, если нечётное, то в добавляемых разрядах все 0 превращаются в 1, а 1 – в 0, т.е. комбинация инвертируется по отношению к исходной. Примеры составления комбинаций инверсного кода из комбинаций семиразрядного двоичного кода представлены в табл. 4.12. Таблица 4.12 Примеры инверсного кода
Декодирование инверсного кода при его приёме осуществляется в два этапа. На первом этапе суммируются единицы в первой половине полной кодовой комбинации. Если сумма единицчётная, то контрольные символы т принимаются без изменений, если нечётная, то символы т инвертируются. На втором этапе контрольные символы т сравниваются с символами k, и при наличии хотя бы одного несовпадения вся переданная комбинация п = k + mэлементов бракуется. Это поэлементное сравнение эквивалентно суммированию по модулю 2. При отсутствии ошибок в обеих половинах символов полной кодовой комбинации их сумма равна нулю. Пусть передана первая комбинация из табл. 4.12. Ниже показано суммирование для трёх вариантов приема переданной комбинации: 1) 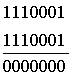 2) 2) 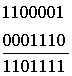 3) 3) 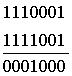 В первом варианте искажений нет и число единиц в информационных символах k четное, поэтому производится суммирование по модулю 2 с неинвертируемыми символами т,что в результате дает нулевую сумму. Во втором варианте число единиц в символах k нечётное, единица в пятом разряде искажена, и символы т инвертированы. В третьем варианте искажение возникло в четвертом разряде группы т. Таким образом, из трех вариантов лишь первый оказался без искажений, а второй и третий должны быть забракованы из-за наличия несовпадения в группах символов k и m. Корректирующие возможности инверсного кода достаточно велики. Этому способствует метод его построения. Добавление т символов приводит к увеличению минимального кодового расстояния. После инвертирования корректирующие возможности кода изменяются в зависимости от числа разрядов исходного двоичного кода. Так, если передаются все комбинации обычного двоичного кода с k = 2 (00, 01, 10 и 11), то этот непомехоустойчивый код, превращаясь в инверсный (0000, 0110, 1001 и 1111), увеличивает минимальное кодовое расстояние до dmin=2и позволяет обнаруживать все одиночные ошибки и 67% двойных ошибок. Действительно, в каждой комбинации может быть С42 = 6 двойных ошибок: так, комбинация 0000 при двойных ошибках примет вид 1100, 0110, 0011, 1001, 1010 и 0101. При этом только второе и четвертое искажения не могут быть обнаружены. У трёхразрядного двоичного кода (000, 001, .. , 111) после преобразования его в инверсный код кодовое расстояние увеличивается до dmin=3. Это значит, что такой код гарантированно обнаруживает все двойные ошибки. Кроме того, он обнаруживает 80% тройных и четверных ошибок и все пяти- и шестикратные ошибки. Четырехразрядный двоичный код (0000, 0001,.... 1111) после преобразования его в инверсный код имеет dmin = 4. Он обнаруживает все ошибки во втором, третьем, пятом, шестом и седьмом символах, не обнаруживает 22% четырехкратных ошибок и совсем не обнаруживает восьмикратные ошибки. Высокие корректирующие возможности инверсного кода достигаются за счет очень большой избыточности. В этом отношении инверсный код значительно уступает другим кодам, о которых будет сказано далее. 4.7. КОДЫ С ОБНАРУЖЕНИЕМ И ИСПРАВЛЕНИЕМ ОШИБОК Если кодовые комбинации составлены так, что отличаются друг от друга на кодовое расстояние d= 3, то они образуют корректирующий код, который позволяет по имеющейся в кодовой комбинации избыточности не только обнаруживать, но и исправлять ошибки. 4.7.1. Коды Хэмминга Для построения кода Хэмминга используется информационная часть в виде двоичного кода на все сочетания с числом информационных символов k, к которой добавляют контрольные символы т. Таким образом, общая длина полной кодовой комбинации n =k + m. Рассмотрим последовательность кодирования и декодирования по Хэммингу. Кодирование кодом Хэмминга предусматривает выполнение следующих этапов. 1. Определение числа контрольных символов. Для этого можно воспользоваться следующими рассуждениями. При передаче по каналу с помехами при единичном искажении может быть искажен любой из п символов кода, всего будет n вариантов искажённых комбинаций. Код может быть передан и без искажений. Таким образом, при единичном искажении может быть n + 1 вариантов передачи, включая передачу без искажений. Используя контрольные символы, необходимо различить все п + 1 вариантов. С помощью контрольных символов m можно описать 2m событий. Значит, должно быть выполнено условие 2m ≥ n + 1=k + m + 1. (4.3) В неравенстве (4.3) по известной величине kнаходится число контрольных разрядов m, необходимых для построения кода, способного обнаружить и исправить заданное число ошибок. В табл. 4.13 представлена зависимость между k и т,полученная из неравенства (4.3). Таблица 4.13 Число контрольных символов в зависимости от числа информационных разрядов для исправления одной ошибки
Число искажённых кодовых комбинаций зависит от кратности искажения и в общем случае определяется по формуле где n – число разрядов полной кодовой комбинации, l – кратность искажения. Неравенство (4.3) в общем случае записывается в виде 2m ≥ Е+1, (4.5) где величина Е определяется (4.4). Формулы (4.4) и (4.5) позволяют определить число контрольных разрядов для искажений произвольной кратности. 2. Размещение контрольных символов. Для удобства обнаружения искаженного символа целесообразно размещать их на местах, кратных степени 2, т.е. на позициях 1, 2, 4, 8 и т.д. Информационные символы располагаются на оставшихся местах. Поэтому, например, для семиэлементной полной кодовой комбинации можно записать m1,m2, k4, m3, k3, k2, k1, (4.6) где k4 – старший (четвертый) разряд информационной кодовой комбинации двоичного кода, подлежащий кодированию; k1 – младший (первый) разряд. 3. Определение состава контрольных символов. Какой из символов должен стоять на контрольной позиции (1 или 0), выявляют с помощью проверочной таблицы. Рассмотрим это на примере комбинации (4.6). Вначале составляется предварительная таблица (табл. 4.14), в которой записаны все кодовые комбинации (исключая нулевую) для трехразрядного двоичного кода на все сочетания и в правом столбце сверху вниз проставлены символы комбинации кода Хэмминга, записанные в последовательности (4.6). Таблица 4.14 Пример предварительной таблицы кода Хэмминга
По предварительной таблице составляется проверочная таблица, в которой выписаны символы кодовой комбинации (4.6) в трех строках, формируемые по следующим правилам. В первую строку записываются символы, против которых проставлены единицы в младшем (первом) разряде комбинации двоичного кода табл. 4.12. Так, в комбинациях 001, 011, 101 и 111 единицы находятся в младших разрядах, поэтому в первой строке проверочной таблицы (см. табл. 4.14) записывается символ т1,против которого стоит единица в комбинации двоичных чисел 001. Далее в первую строку записывается символы k4, k3 и k1. Во вторую строку проверочной таблицы записываются символы, против которых проставлены единицы во втором разряде двоичного кода. Так, комбинации 010, 011, 110 и 111 содержат во втором разряде 1, поэтому вторая строка проверочных коэффициентов состоит из символов m2, k3,k2и k1. В третью строку записываются символы, против которых проставлены единицы в третьем разряде двоичного кода, это символы т3, k3, k2 и k1. Таблица 4.15 Проверочная таблица кода Хэмминга
Число строк в проверочной табл. 4.15 равно числу контрольных символов т. В случае кодирования более длинных информационных кодовых комбинаций табл. 4.14 и 4.15 должны быть расширены, так как должны быть записаны четвертая, пятая и т.д. строки проверочных коэффициентов. Для этого нужно лишь увеличить число разрядов двоичного кода в табл. 4.14. Например, для комбинации т1,m2,k11, m3, k10, k9,k8,m4,k7,k6,k5,k4,k3,k2,k1, имеющей одиннадцать информационных символов и четыре контрольных символа, табл. 4.14 будет содержать 15 строк, а табл. 4.15 будет состоять из четырёх строк. Состав контрольных символов с помощью проверок определяют следующим образом. Суммируют информационные символы, входящие в каждую строку табл. 4.15; если сумма единиц в данной строке четная, то значение символа т,входящего в эту строку, равно 0, если нечетная, то 1. По первой строке табл. 4.15 определяют значение символа т1,по второй – т2,по третьей – m3. Полученные по табл. 4.15 контрольные символы подставляют в полную кодовую комбинацию (4.6) кода Хэмминга, которая теперь полностью определена. Пример 4.1 Закодировать кодом Хэмминга, исправляющим одну ошибку, информационную комбинацию двоичного кода 1101. В информационной комбинации содержится четыре информационных разряда, т.е. k=4. Согласно табл. 4.13 число контрольных символов m=3, и в соответствии с (4.6) размещаются они на позициях 1, 2 и 4, а информационные символы – на позициях 3, 5, 6 и 7 полной кодовой комбинации, в которой всего семь разрядов, так как n=k+m. Символы информационной части известны, а контрольные символы необходимо определить. Полную кодовую комбинацию можно записать в виде: т1m2 k4 m3 k3k2 k1 ? ? 1 ?1 0 1 Для определения контрольных символов заполняем табл. 4.15 значениями информационных символов и в полученной таким образом табл. 4.16 суммируем по модулю 2 информационные символы каждой строки. Таблица 4.16 Проверочная таблица кода Хэмминга, заполненная информационными символами 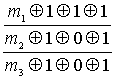 Очевидно, что суммирование информационных символов первой строки даёт 1, суммирование этих символов второй и третьей строк даёт 0. Следовательно, имеем следующий состав контрольных символов:т1 =1, m2 =0, m3=0. Подставляя контрольные символы на их позиции в (4.6), получим полную кодовую комбинацию кода Хэмминга: 1 0 1 0 1 0 1. Декодирование кода Хэмминга. Для обнаружения и исправления ошибки выполняются следующие действия. 1. Заполнение проверочной таблицы символами полной кодовой комбинации Проверочная таблица кода Хэмминга (см. табл. 4.15) заполняется символами полной кодовой комбинации с использованием структуры (4.6) этой комбинации. 2. Суммирование по модулю 2 строк проверочной таблицы Символы всех строк проверочной таблицы суммируются по модулю 2. Если результат суммирования по всем строкам нулевой, то в принятой комбинации искажений нет. Наличие ненулевого результата означает наличие искажений. 3. Определение места искажения Место искажения определяется двоичным числом, являющимся результатом суммирования. Для этого столбец результата суммирования читается по вертикали снизу вверх, так что старшим разрядом двоичного числа является результат суммирования последней строки проверочной таблицы, а младшим разрядом – результат суммирования первой строки проверочной таблицы. 4. Исправление искажения Для исправления искажения полученное двоичное число переводят в десятичное, которое означает номер разряда полной кодовой комбинации, включая контрольные разряды, в котором имеется искажение. Счёт разрядов ведётся слева направо. Принятый символ этого разряда заменяется противоположным, т.е. 0 заменяется на 1 или 1 заменяется на 0. Получается неискажённая кодовая комбинация. Контрольные символы в соответствии с (4.6) отбрасываются, неискажённая информационная часть обрабатывается. Пример 4.2 Принята кодовая комбинация 1010111. Известно, что она закодирована кодом Хэмминга, исправляющим одну ошибку. Определить, есть ли в ней искажение, и если есть, то исправить его. Принятая кодовая комбинация имеет 7 разрядов, поэтому согласно табл. 4.11 в ней имеется 4 информационных символа и 3 контрольных. Структура такой комбинации имеет вид (4.6):
Проверочная таблица семиразрядного кода Хэмминга имеет вид табл. 4.15. Подстановка в неё символов принятой комбинации даёт табл. 4.17. Таблица 4.17 Проверочная таблица принятой кодовой комбинации примера 4.2 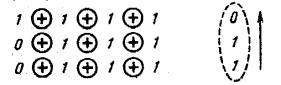 Результат суммирования по модулю 2 строк этой таблицы приведен в правом столбце: первая строка даёт нулевой результат, вторая и третья строки дают единичный результат. Такой результат свидетельствует о наличии искажения. Для исправления ошибки результат суммирования читается по вертикали снизу вверх. Это даёт двоичное число 110, ему соответствует десятичное число 6. Полученный результат означает, что искажён шестой разряд принятой кодовой комбинации, считая слева направо. Искажён разряд k2.Поэтому принятый символ этого разряда, равный 1, заменяется на символ 0, получена исправленная (неискажённая) кодовая комбинация 1010101. Отбрасываются контрольные символы первой, второй и четвёртой позиций полной кодовой комбинации, неискажённая информационная комбинация имеет вид 1101 (см. пример 4.1). Итак, для повышения помехоустойчивости кода необходимы дополнительные контрольные символы, которые увеличивают длину кодовой комбинации. Например, семиразрядный код обеспечивает передачу 27=128 кодовых комбинаций, однако количество информационных символов в семиразрядном коде Хэмминга k = 4, т.е. полезных информационных посылок всего Nk =24=16. Остальные 112 кодовых комбинаций из 128 предназначены для обеспечения помехоустойчивости кода, являются запрещенными и не используются. Выше был рассмотрен код Хэмминга с исправлением одиночной ошибки. Такие коды применяют в том случае, если статистика показывает, что наиболее вероятны одиночные искажения в канале связи. Однако если вероятность искажения двух символов в кодовой комбинации велика, то целесообразно применение кода Хэмминга, позволяющего исправить одиночные ошибки, если была только одиночная ошибка, и, кроме того, обнаружить двойные ошибки, если были две ошибки. Для построения такого кода число контрольных символов определяется не по табл. 4.13, а по формулам (4.3), (4.4), (4.5). Имеются и частные приёмы построения кодов Хэмминга с повышенными корректирующими способностями. Например, код Хэмминга, позволяющий исправить единичные ошибки, если была только одиночная ошибка, и, обнаружить двойные ошибки, если были две ошибки, строится на базе кода, исправляющего единичные ошибки. Для этого к полной кодовой комбинации кода Хэмминга добавляется контрольный символ, дополняющий до чётности всю комбинацию, включая этот символ. Контрольный символ должен быть равен единице, если число единиц в закодированной комбинации (4.6) нечетное, и нулю, если число единиц четное. В табл. 4.18 приводится несколько комбинаций четырехразрядного двоичного кода, закодированных для исправления одиночной ошибки, с добавлением дополнительного контрольного разряда mдоп, с целью проверки этих комбинаций на четность. При декодировании принятой комбинации возможны следующие варианты. 1. Ошибок нет (прием верен). В таком случае как проверка на чётность расширенной кодовой комбинации, так и проверка по проверочной таблице дают нулевые суммы. Все контрольные разряды, включая mдоп, отбрасываются. Таблица 4.18 Примеры кодов Хэмминга, обнаруживающих две ошибки и исправляющих одну ошибку
2. Имеется единичная ошибка. В таком случае проверка на чётность расширенной кодовой комбинации показывает наличие ошибки (сумма единиц по модулю 2, входящих в кодовую комбинацию, не дает нуль). Декодирование по проверочной таблице без разряда mдоп указывает на номер искаженного символа, который нужно заменить на противоположный. 3. Имеются две ошибки. Проверка на чётность расширенной кодовой комбинации указывает на отсутствие ошибок, а декодирование по проверочной таблице – на наличие ошибки. В результате декодирования указывается номер позиции, где якобы возникла ошибка, однако её не следует исправлять, а лишь констатировать наличие двух ошибок). Добавление дополнительного контрольного символа mдоп к закодированной для исправления одиночной ошибки кодовой комбинации увеличивает кодовое расстояние с d=3до d =4, так как r = 2, s= 1, а d = 2 + 1 + 1=4. 4.7.2. Циклические коды Эти коды широко применяются в аппаратуре передачи данных и системах телемеханики благодаря высокой эффективности [9]. Простота аппаратной реализации на регистрах сдвига и ячейках сумматора по модулю два в своё время обеспечила им широкое применение, а сравнительно небольшая избыточность делает их эффективными в настоящее время. Кодовая комбинация имеет информационные и контрольные разряды, последние помещаются в конце комбинации, т.е. коды являются систематическими, равномерными, обозначаются (n, k), где n – полное число разрядов, k – число информационных разрядов. Информационной частью служит натуральный двоичный код. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
