|
|
ТОК Лекции. Конспект лекций Самара Самарский государственный технический университет 2011
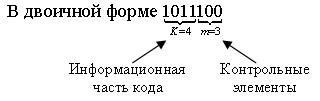 Принципы построения циклических кодов.
Определенные комбинации циклического кода можно значительно упростить, если применить способ записи натурального двоичного кода с помощью единичной транспонированной матрицы.
Таблица 4.19
Единичная и единичная транспонированная матрицы
четырёхразрядного двоичного кода

Определяющей матрицей натурального двоичного k – разрядного кода является квадратная единичная матрица Ik или единичная транспонированная матрица IkT, имеющая k – столбцов и k – строк. Разница между этими матрицами в том, какая из главных диагоналей имеет все элементы, равные 1 (табл. 4.19).
Из матрицы Ik или IkT путем сложения нескольких строк по модулю 2 в различных сочетаниях можно получить все ненулевые комбинации кода.
При использовании этого способа записи достаточно многочлены, образуемые строками IkT, умножить на xn-k, разделить на P(x) и остаток приписать в виде дополнительной матрицы C(n-k), k контрольных элементов. Тогда определяющую матрицу C* циклического (n, k) кода можно записать в следующем виде:
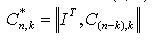 . (4.10) . (4.10)
Пример 4.4
Построить циклический (7, 4) код для образующего многочлена P(x)=х3+x2+1.
У этого кода n=7, k=4, m=3. Для построения используем единичную транспонированную матрицу.
Первая строка этой матрицы G(x)=1, поэтому G(x)*x3= x3. Далее выполняем деление на образующий многочлен и для этой строки получаем остаток 101 (табл. 4.20). Здесь же приведены результаты деления, выполняемого для других строк матрицы.
Вторая строка матрицы G(x)= x, поэтому G(x)*x3= x4. Деление на образующий многочлен даёт для этой строки остаток 111.
Аналогичные действия для третьей строки дают остаток 011, для четвёртой строки – остаток 110 .
Полученные остатки запишем в форме дополнительной матрицы контрольных элементов (табл. 4.21).
Вместо четырех операций деления можно провести одну, взяв в качестве делимого первую строку единичной матрицы Ik, умноженную на 1000 (х3) (табл. 4.22).
Таблица 4.20
Получение остатков для строк единичной транспонированной матрицы

Таблица 4.21
Дополнительная матрица контрольных элементов
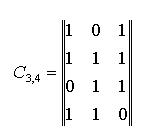
Выписывая все частные остатки, получим дополнительную матрицу С3,4 для циклического кода (см. табл. 4.21).
Объединение единичной транспонированной матрицы с матрицей остатков даёт определяющую матрицу С*7,4 четырёхразрядного циклического кода (табл. 4.23).
Таблица 4.22
Получение частных остатков для единичной матрицы

Таблица 4.23
Определяющая матрица четырёхразрядного циклического кода
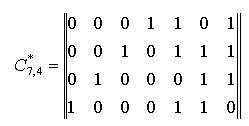
Из определяющей матрицы С*7,4 находят ненулевые комбинации путем сложения строк в различных сочетаниях.
Пример 4.5
Найти кодовую комбинацию циклического (7, 4) кода для информационной комбинации 1011 и образующего многочлена P(x)=х3+x2+1.
Информационная кодовая комбинация 1011 получается сложением первой, второй и четвёртой строк единичной транспонированной матрицы. Поэтому, складывая эти строки определяющей матрицы четырёхразрядного циклического кода, получаем кодовую комбинацию 1011100, что совпадает с результатом кодирования примера 4.3.
|
|
|
 Скачать 6.93 Mb.
Скачать 6.93 Mb.