ТОК Лекции. Конспект лекций Самара Самарский государственный технический университет 2011
 Скачать 6.93 Mb. Скачать 6.93 Mb.
|
Образующий многочлен.Выбирается из числа неприводимых многочленов, некоторые из которых представлены в табл. 4.24. Таблица 4.24 Неприводимые многочлены 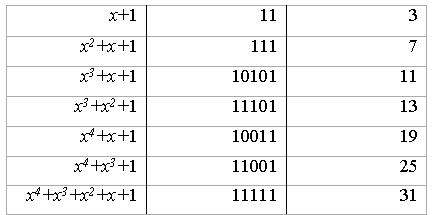 Он должен иметь порядок (n-k)=m и входить в качестве сомножителя в состав двучлена (xn+1). Выбор P(x) влияет на корректирующие возможности циклического кода. Однократные и двукратные ошибки позволяют обнаружить следующие полиномы (табл. 4.25). Таблица 4.25 Образующие многочлены для обнаружения единичных и двойных ошибок
Для обнаружения ошибок принятая комбинация циклического кода делится на образующий многочлен. Если результат не имеет остатка, то искажений нет, контрольные символы отбрасываются, и декодируется информационная часть. Если имеется искажение, то искаженная комбинация: H(x)=F(x)+E(x), где E(x) – многочлен ошибок, содержащий столько «1», сколько элементов искажено. Для обнаружения и исправления ошибок существует несколько вариантов декодирования. Один из них заключается в следующем: 1. Вычисление остатка (как и при обнаружении ошибок). 2. Подсчет веса остатка w. Если w<=s (число исправляемых ошибок), то принятую комбинацию складывают по mod 2 с остатком и получают исправленную комбинацию. 3. Если w>s, то производят циклический сдвиг вправо (с переносом единицы из старшего разряда) на 1 разряд и полученную комбинацию делят на образующий многочлен. Если вес полученного остатка w1<=s, то циклически сдвинутую комбинацию суммируют по mod 2 с остатком R1 и затем циклически сдвигают ее в обратную сторону на 1 символ (на прежнее место), получают исправленную комбинацию. 4. Если одного сдвига вправо недостаточно, то сдвиг повторяют до тех пор, пока wi<=s, затем исправленную комбинацию возвращают на прежнее место.
Применяются для повышения корректирующих способностей. Пусть требуется применить 15 комбинаций и исправить две ошибки, т.е. s=2, d=5. Код (7, 4) может исправить только одну ошибку. В циклическом коде число разрядов может быть лишь 15, поэтому требуется циклический код (15, 7). Но в нем различных комбинаций 27>>15, поэтому код (15, 7) укорачивают так, чтобы образовать 15 комбинаций. Образующая матрица укороченного (12, 4) псевдоциклического кода имеет следующий вид (табл. 4.26). Восемь контрольных разрядов укороченного циклического кода позволяют исправлять две ошибки, полное число ненулевых кодовых комбинаций равно пятнадцати. Таблица 4.26 Образующая матрица укороченного (12, 4) псевдоциклического кода  4.7.3. Итеративные коды Эти коды могут обнаруживать и исправлять все одиночные ошибки. Простейший вариант итеративного кода является развитием обычного кода с проверкой на чётность. Правила кодирования рассмотрим на примере. 1. Пусть кодовая комбинация, подлежащая кодированию, имеет вид
2. Разбиваем эту комбинацию поровну и записываем в две строки:
3. Делаем проверку на четность символов каждой строки и дописываем справа (или слева) контрольные символы т:
4. Делаем еще одну проверку на четность символов каждого столбца и дописываем внизу или вверху символы m:
В результате этих преобразований получаем итеративный код с равным числом информационных и контрольных символов, в данном случае код (12,6), который можно записать в форме матрицы (4.11) или развернуть в строку (4.12). k6 k5 k4m1 k3 k2 k1 m2 m3 m4m5m6 (4.11) Матрица разворачивается в строку и получается полная кодовая комбинация (4.12) итеративного кода. k6 k5k4 m1 k3 k2 k1 m2m3m4m5 1 0 1 0 0 1 0 1 1 1 1 (4.12) Сделаем проверку на исправление искажения. Предположим, что при передаче произошло искажение и получена комбинация 101011011111. Декодирование осуществляется следующим образом. 1. Полученная кодовая комбинация записывается в форме матрицы в соответствии с (4.11):
2. Делаем проверку на чётность символов каждой строки и каждого столбца, результаты проверки записаны в правом столбце и нижней строке:
Если бы искажения не было, то в каждой строке и в каждом столбце результаты были бы нулевые. Однако в первом столбце и во второй строке имеем ненулевые результаты, что означает наличие искажения. По матрице (4.11) определяем, что в этих двух ненулевых результатах участвовал символ k3. Замена этого символа на обратное значение исправляет ошибку. Итеративные коды обладают очень большой избыточностью и уступают кодам Хэмминга и циклическим кодам. Кроме того, очевидно, что при наличии двух искажений в строке или столбце матрицы (4.11) итеративные коды их не обнаруживают. Поэтому они имеют очень ограниченное применение. КЛЮЧЕВЫЕ ТЕРМИНЫ И ПОНЯТИЯ |
