ТОК Лекции. Конспект лекций Самара Самарский государственный технический университет 2011
 Скачать 6.93 Mb. Скачать 6.93 Mb.
|
|
Примеры единично-десятичного кода
4.4.4. Двоичный нормальный (натуральный) код Этот код имеет широкое распространение в различных областях цифровой техники. Он называется нормальным (натуральным) потому, что весовой коэффициент младшего разряда у него равен единице, а весовой коэффициент каждого последующего разряда по сравнению с предыдущим возрастает в два раза. Максимально возможное число комбинаций двоичного кода N=2n, где n – количество разрядов. Вес старшего разряда равен 2n-1. Таблица четырёхразрядного двоичного натурального кода представлена в табл. 4.5. Таблица 4.5 Таблица четырёхразрядного двоичного натурального кода
Достоинства двоичного кода: 1. Высокая надежность передачи кодовых символов по сравнению с кодами, имеющими большее основание. 2. Простота аппаратной реализации кодовых комбинаций. Недостаток – плохая ассоциативная значимость кодовых комбинаций для человека по сравнению с десятичным кодом. 4.4.5. Двоично-десятичные коды Каждый разряд десятичного числа записывается в виде комбинаций двоичного кода, десятичный разряд отображается четырьмя двоичными разрядами. Таблица 4.6 Примеры двоично-десятичного кода с весовыми коэффициентами 8-4-2-1
Четыре двоичных разряда, отображающие один десятичный разряд, называются тетрадой. Число тетрад двоично-десятичного кода равно числу отображаемых десятичных разрядов. Двоично-десятичный код соединяет в себе достоинства двоичного кода с лучшей ассоциативностью для человека. Лучшая ассоциативная значимость формируется благодаря тому, что пользователь легко может запомнить девять ненулевых кодовых комбинаций двоичного кода, используемых для отображения одного десятичного разряда. Именно поэтому данный код получил широкое распространение. Приведенный выше в табл. 4.6 пример двоично-десятичного кода дан для весовых коэффициентов 8-4-2-1, применяемых для кодирования одного десятичного разряда. Эти весовые коэффициенты однозначно определяют любое десятичное число. Иногда применяют двоично-десятичные коды с другими весовыми коэффициентами, например 2-4-2-1 или 4-2-2-1. С помощью этих весовых коэффициентов одно и тоже десятичное число можно записать несколькими кодовыми комбинациями (табл. 4.7). Таблица 4.7 Таблица двоично-десятичных кодов
Код 4-2-2-1 обладает свойством самодополняемости, которое означает, что кодовая комбинация, полученная из исходной путем замены 0 на 1 и 1 на 0 (инвертированный код) в каждом разряде, всегда дополняет исходное число до 9 (1111). Благодаря этому свойству указанные коды и получили распространение в телемеханике. Двоично-десятичный код с весами 7-4-2-1 в каждой кодовой комбинации имеет не более двух единиц, что позволяет использовать это свойство для повышения помехоустойчивости передачи. 4.4.6. Код Грея В некоторых измерительных устройствах, входящих в состав систем телемеханики, применяется преобразование измеряемой физической величины сразу в кодовую комбинацию без предварительного преобразования в электрическую величину и без использования аналого-цифрового преобразователя. С этой целью физическая величина преобразуется в угловое или линейное перемещение, которое затем преобразуется в код. На рис. 4.3, а представлен кодирующий диск с маской обычного двоичного кода. Поверхность концентрических окружностей разбивается по определенному правилу на ряд участков, светлые из которых представляют собой двоичную цифру 1, а темные – 0. Каждая окружность или кольцо диска соответствует разряду двоичного числа; внутреннее кольцо соответствует старшему разряду, наружное – младшему. Этот диск является кодирующим устройством (кодером, шифратором) для образования четырехразрядных кодовых комбинаций. Его построение соответствует форме записи комбинаций четырёхразрядного двоичного кода на все сочетания. Из табл. 4.5 следует, что в старшем разряде четырёхразрядного кода переход от нуля к единице происходит лишь один раз; сначала идет восемь раз 0, а затем восемь раз 1. По этому же принципу выполнено и внутреннее кольцо диска: половина его окружности темная (заштрихованная), что соответствует нулям, а половина – светлая для формирования единиц. В третьем разряде этого кода чередование единиц и нулей происходит в два раза чаще, поэтому во втором кольце (считая от центра) имеются два сплошных заштрихованных сегмента для нулей и два полых – для единиц. По такому же принципу соответствия двоичному коду третье кольцо разделено на восемь частей, а четвертое наружное – на 16. Если необходимо передать изменение угла двоичными комбинациями, равными не 16, а 32, то следует добавить снаружи еще одно кольцо, разделенное на 32 части. 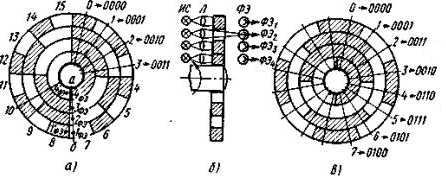 Рис. 4.3. Кодирующий диск: а – маска двоичного кода; б – считывание показаний диска, в – диск с маской четырехразрядного кода Грея Кодирующий диск располагается на оси, которая совершает определенные угловые перемещения в зависимости от изменения измеряемой величины. С одной стороны диска расположены источники света ИС с оптическими системами (линзами) Л, направляющими пучки света через отверстия в диске на фотоэлементы ФЭ (рис. 4.3, б), где показан диск в разрезе. Сигналы возникают на выходе тех фотоэлементов, которые в данном положении диска получают свет через прозрачные (нулевые) участки диска. При положении диска, указанном на рисунке, считывается цифра 2, так как на первый, третий и четвертый фотоэлементы луч света не попадает, что соответствует 0 в младшем и двух старших разрядах, а засветка второго фотоэлемента посылает на выход одну единицу. Таким образом, на выходе регистрируется кодовая комбинация 0010. Фотоэлементы должны располагаться точно по радиальной линии во избежание ошибки при отсчитывании. Действительно, в зависимости от точности установки фотоэлемента при переходе от одного значения к другому может возникнуть погрешность в любом разряде. Так, если установка точная, то при подходе к сектору с числом 8 (положения засветки фотоэлементов 1ФЭ-4ФЭ) будет сниматься число 0111 (линия а – б на рис. 4.3, а), т.е. 7 в десятичном эквиваленте. Если фотоэлемент ФЭ4 выдвинут вперед (положение засветки 4ФЭ) по отношению к остальным трем фотоэлементам, то будет считано число 1111 (вместо 0111), т.е. 15 в десятичной системе счисления. Если вперед выдвинут фотоэлемент ФЭ1 (положение засветки 1ФЭ), то считывается число 0110, т.е. 6. Соответственно могут быть погрешности в установке и других фотоэлементов. Таким образом, при использовании маски обычного двоичного кода ошибка может быть минимальной, если она возникает в младшем (первом) разряде, и максимальной – в старшем разряде. В общем случае при искажении во всех разрядах максимальная ошибка составит 2n-1 + 2n-2 +…+ 21 + 20 . Во избежание подобных ошибок вместо обычного двоичного применяют коды, в которых при переходе от одного числа к другому комбинация изменяется только в одном разряде, и, следовательно, кодовая маска составляется так, что это изменение в любом разряде может дать погрешность лишь на единицу. Такие коды называются однопеременными, к ним относится код Грея. Код Грея уменьшает указанную погрешность до 2n-1 . Код Грея для десятичных чисел от 0 до 15 представлен в табл. 4.8, из которой следует, что две соседние комбинации отличаются одна от другой только в одном разряде. Таблица 4.8 Таблица кода Грея
Многоразрядный двоичный код преобразуется в код Грея по следующему правилу. Преобразуемая кодовая комбинация двоичного кода суммируется по модулю 2 с кодовой комбинацией, полученной из исходной, путём сдвига влево (в сторону младшего разряда) на один разряд. В полученной сумме младший разряд отбрасывается, оставшаяся часть суммы представляет собой код Грея. Например, преобразование двоичных чисел 1101 и 1010 в код Грея производится следующим образом: 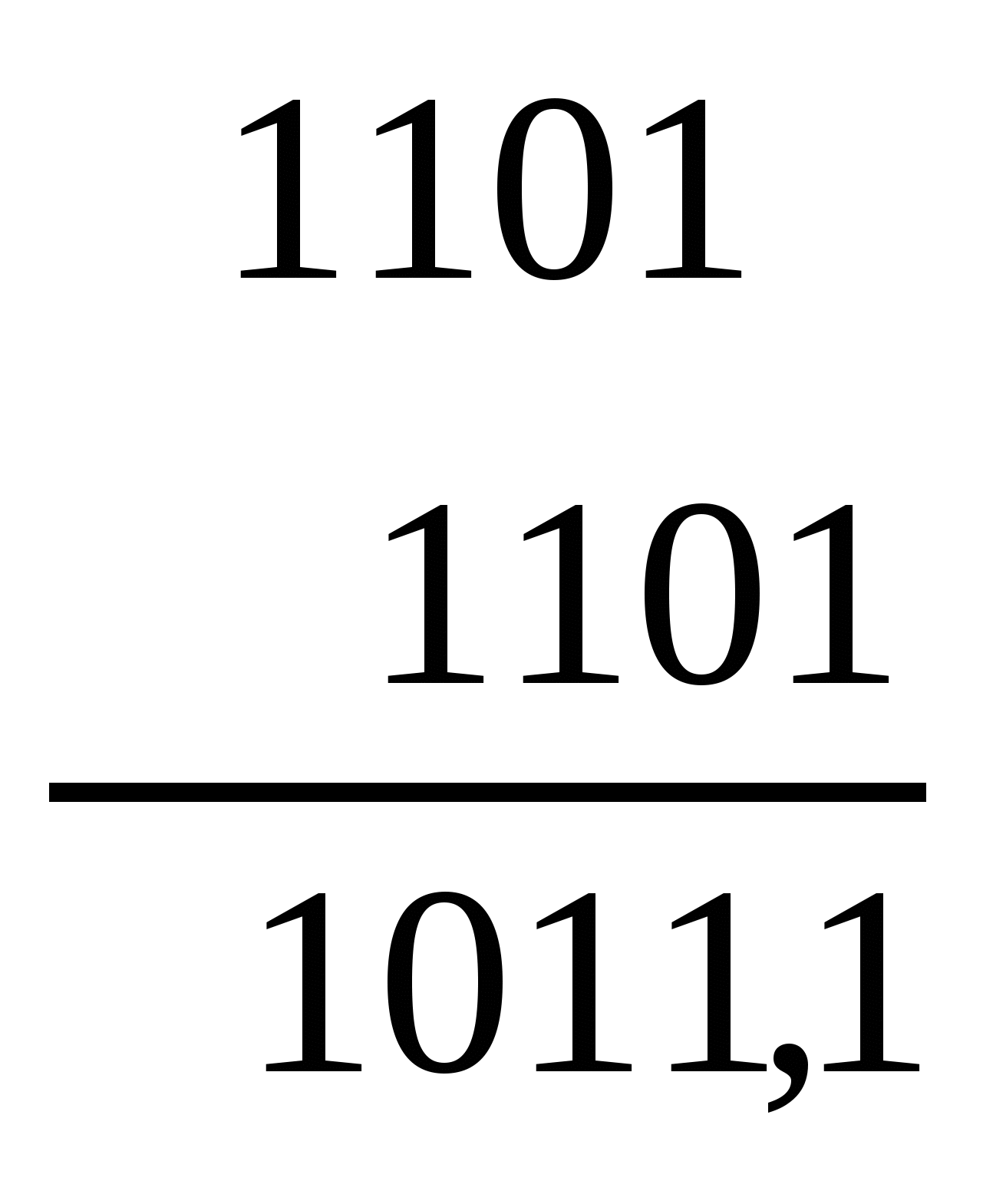 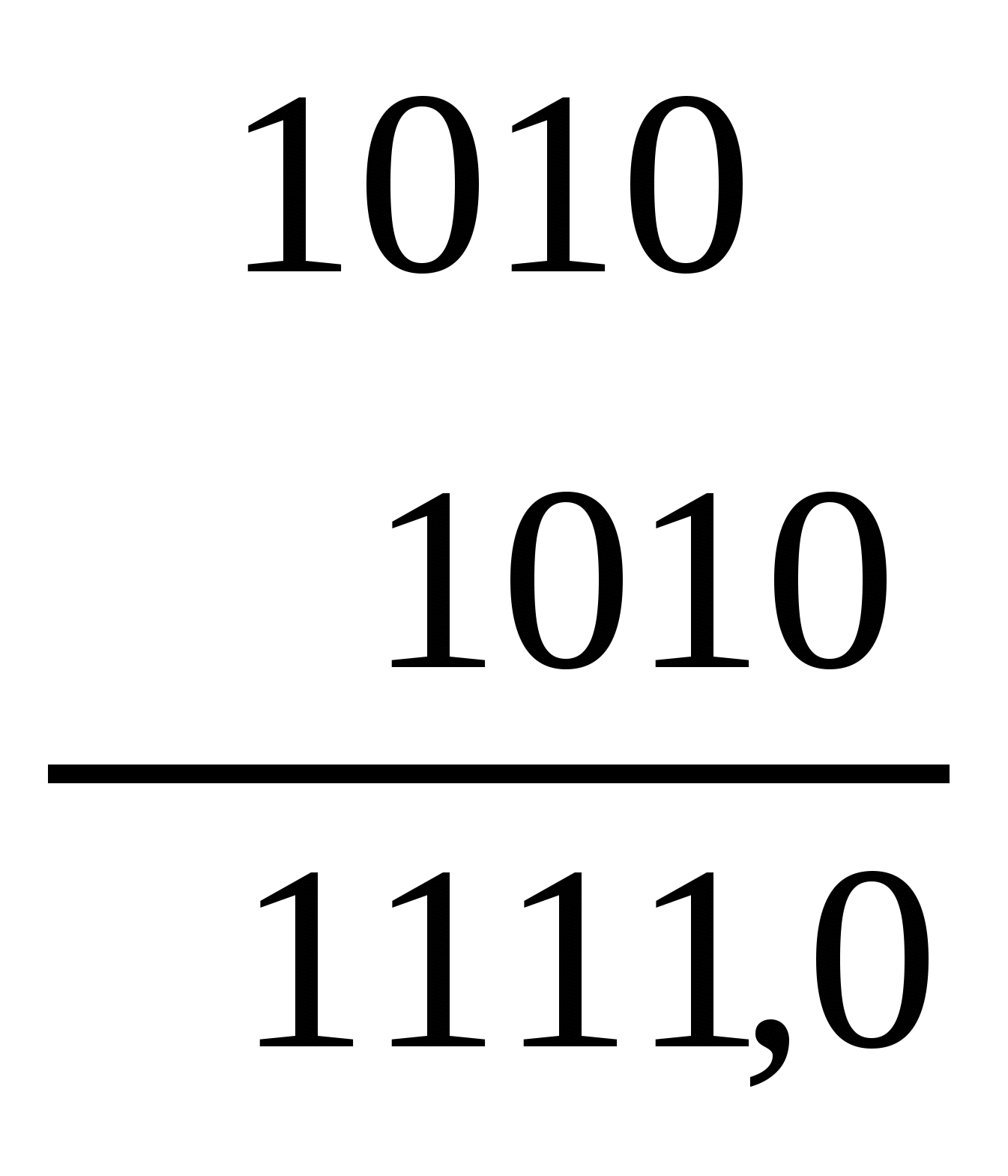 Преобразование двоичного числа в код Грея можно осуществить и по следующему принципу. Если в старшем, соседнем по отношению к данному, разряде двоичного числа стоит 0, то в данном разряде кода Грея сохраняется цифра, записанная в двоичном коде, если же 1, то цифра меняется на обратную. Например, при переводе той же комбинации двоичного кода 1101 в младшем разряде кода Грея сохранится 1, так как в соседнем (втором) разряде двоичного числа записан 0. Во втором разряде кода Грея 0 изменится на 1, так как в третьем разряде двоичного кода записана 1. В третьем разряде 1 заменится на 0 из-за того, что в четвертом разряде двоичного кода стоит 1, а в четвертом разряде кода Грея останется 1, так как подразумевается, что левее четвертого разряда двоичного числа стоит символ 0. Преобразование кода Грея в двоичный код производится по следующему правилу. 1. Преобразование выполняется поразрядно. 2. Преобразование начинается со старшего разряда, который остаётся неизменным. 3. Символ преобразуемого последующего разряда определяется суммой сложения по модулю 2 символов преобразуемой комбинации, начиная со старшего разряда и заканчивая преобразуемым разрядом. Если при сложении по модулю 2 сумма оказывается четной, то в преобразуемом разряде записывается 0, если нечетной – то записывается 1. Пусть, например, преобразуется комбинация кода Грея 1011 в двоичный код. Старший (четвёртый) разряд двоичного кода имеет символ 1. Третий разряд имеет символ 1, так как Непосредственное преобразование кода Грея в десятичное число представляет определенные трудности, и зачастую проще осуществить двойное преобразование: сначала преобразовать код Грея в двоичный, а затем двоичный код – в десятичный. Сложность преобразования в десятичный эквивалент является недостатком кода Грея. 4.5. КОРРЕКТИРУЮЩИЕ КОДЫ. ПРИНЦИПЫ ОБНАРУЖЕНИЯ И ИСПРАВЛЕНИЯ ОШИБОК Корректирующими (или помехозащищёнными) называются коды, позволяющие обнаружить и исправить ошибки в кодовых комбинациях. Отсюда и деление этих кодов на две большие группы: 1. Коды с обнаружением ошибок. 2. Коды с обнаружением и исправлением ошибок. Принципы обнаружения и исправления ошибок кодами хорошо иллюстрируются с помощью геометрических моделей. Любой n-элементный двоичный код можно представить n-мерным кубом (см. рис. 4.2), в котором каждая вершина отображает кодовую комбинацию, а длина ребра куба соответствует одной единице. В таком кубе расстояние между вершинами (кодовыми комбинациями) измеряется минимальным количеством ребер, находящихся между ними, обозначается dи называется кодовым расстоянием Хэмминга. Кодовое расстояние (или минимальное кодовое расстояние) – это минимальное число элементов, в которых любая кодовая комбинация отличается от другой (по всем парам кодовых комбинаций). Например, код состоит из комбинаций 1011, 1101, 1000 и 1100. Сравнивая первые две комбинации, находим, что d = 2. Сравнение первой и третьей комбинаций показывает, что и в этом случае d = 2.Наибольшее значение d = 3обнаруживается при сравнении первой и четвертой комбинаций, а наименьшее d = 1 – второй и четвертой, третьей и четвертой комбинаций. Таким образом, для данного кода минимум расстояния dmin =1. При п = 1n-мерный куб превращается в прямую длиной d = 1,на одном конце которой располагается 1, а на другом – 0. При п = 2 четыре возможные комбинации (N=22=4) располагаются на четырех вершинах квадрата. При этом комбинации 00 и 11, а также 10 и 01 отличаются друг от друга в двух разрядах, т.е. d =2. Кодовое расстояние между двумя комбинациями двоичного кода равно числу единиц, полученных при сложении этих комбинаций по модулю 2. Как известно, суммирование по модулю 2 осуществляется по следующим правилам: Такое определение кодового расстояния удобно при большой разрядности кодов. Так, складывая по модулю 2 комбинации 10110101101 и 10000000010, определяем, что кодовое расстояние между ними d = 7.  При n= 3 восемь кодовых комбинаций размещаются в вершинах трехмерного куба. Трехмерный куб строится так (см. рис. 4.2), что одна из его вершин лежит в начале координат. Каждой вершине куба приписывается кодовая комбинация по следующему правилу: на i-том месте кодовой комбинации ставится 0, если проекция этой вершины на i-туюось координат равна нулю, и 1, если проекция равна единице. Например, требуется узнать, какую следует записать комбинацию в вершине А6(см. рис. 4.2). Проецируя эту вершину на ось Х1,получим единицу. На втором месте комбинации запишется также 1 (проекция на ось Х2 равна единице). Так как проекция на ось Х3 равна нулю (проекция в начало координат), то на третьем месте комбинации запишется 0. Следовательно, вся комбинация в вершине A6 запишется как 110. Если использовать все восемь слов, записанных в вершинах куба, то образуется трёхразрядный двоичный код на все сочетания. Такой код не является помехоустойчивым, так как при искажении любого разряда одна кодовая комбинация переходит в другую и выявить это искажение невозможно. Если же уменьшить число используемых комбинаций с восьми до четырех, то появится возможность обнаружения одиночных ошибок. Для этого выберем только такие комбинации, которые отстоят друг от друга на расстояние d = 2,например 000, 110, 011 и 101. Остальные кодовые комбинации не используются. Если будет принята комбинация 100, то очевидно, что при ее приеме произошла одиночная ошибка. Представленные комбинации построены по определенному правилу, а именно содержат четное число единиц, а принятая комбинация 100 – нечетное. Можно утверждать, что комбинация 100 образовалась при искажении разряда одной из разрешенных комбинаций, но определить, какая именно комбинация искажена, невозможно. Поэтому такие или подобные им коды называют кодами с обнаружением ошибок. Кроме указанной группы комбинаций в том же трехмерном кубе может быть получена еще одна группа комбинаций с кодовым расстоянием d = 2(111, 001, 010 и 100). В этих кодовых комбинациях нечетное число единиц и каждая из комбинаций могут быть использованы для обнаружения ошибки, возникшей при передаче, так как при одиночном искажении в комбинации будет четное число единиц. Если необходимо получить код с обнаружением одиночной ошибки, то можно использовать только одну группу, т.е. четыре комбинации из возможных восьми. В противном случае получится непомехоустойчивый код, в котором используются комбинации с d = 1. Таким образом, в помехозащищённых кодах есть комбинации разрешенные, составленные по определенному правилу, и запрещенные, не соответствующие этому правилу. Четыре из восьми комбинаций трехразрядного кода, позволяющие обнаружить одиночную ошибку (например, 111, 001, 010 и 100), называются разрешенными, а остальные четыре (000, 011, 101 и 110) – запрещенными, которые должны интерпретироваться при приеме как искаженные. Построение помехоустойчивого кода связано с недоиспользованием кодовых комбинаций, приводящим к так называемой избыточности. Избыточность означает, что из исходных символов можно построить больше комбинаций, чем их применено в данном коде. Таким образом, установлено, что уменьшение числа используемых комбинаций приводит к повышению помехоустойчивости кода. Если еще больше ограничить число разрешенных комбинаций, то можно создать код не только с обнаружением, но и с исправлением ошибки. Выберем в трехмерном кубе такие вершины, кодовые обозначения которых отличались бы друг от друга на d = 3. Такие вершины расположены на концах пространственных диагоналей куба. Их может быть только четыре пары: 000 и 111, 001 и 110, 100 и 011, 010 и 101. Однако из этих четырех пар для передачи можно брать только одну любую пару, так как большее число пар приведет к тому, что в передаче будут использоваться комбинации, отличающиеся друг от друга на d < 3. Код, образованный по такому правилу, может исправить одиночную ошибку или обнаружить две ошибки без их исправления. Пусть, например, передается код, состоящий из комбинаций 001 и 110. На приеме получена комбинация 100. Сравнение ее с исходными комбинациями показывает, что от комбинации 110 она отличается в одном (втором) разряде, а от комбинации 001 – в двух разрядах. Если считать, что сделана одна ошибка, то полученную комбинацию 100 следует исправить на 110. От разрешенной комбинации 001 отличаются на d = 1 комбинации 011, 000 и 101, а от комбинации 110 – комбинации 111, 100 и 010. Они и являются своеобразными комбинациями-спутниками, которые после приема можно относить к той или иной исходной комбинации. Когда говорят об исправлении одиночной ошибки, то считают, что вероятность двойной ошибки при передаче кодовой комбинации пренебрежимо мала. Если такая вероятность достаточно велика, то код с d = 3 можно использовать для обнаружения двойных ошибок, но при этом исправить одиночную ошибку он уже не может. Действительно, если в рассмотренном примере была принята комбинация 100, то нельзя утверждать, что была передана комбинация 110, так как при двойных ошибках это могла быть и искаженная комбинация 001. Таким образом, дальнейшее повышение помехоустойчивости кода связано с увеличением кодового расстояния d, что приводит к увеличению избыточности (вместо восьми комбинаций используются только две). Корректирующая способность кода зависит от кодового расстояния: 1) при d = 1 ошибка не обнаруживается; 2) при d = 2 обнаруживаются одиночные ошибки; 3) при d = 3 исправляются одиночные ошибки или обнаруживаются двойные ошибки. В общем случае d =r + s+ 1, r >= s,(4.1) где d – минимальное кодовое расстояние, r – число обнаруживаемых ошибок, s – число исправляемых ошибок. При этом обязательным условием является r >= s. Так, в рассмотренном выше примере d= 3, и если r = s = 1, то код может обнаружить одну ошибку и исправить ее. Если r = 2, s = 0, то код может только обнаружить две ошибки. Для исправления одной ошибки и обнаружения двух ошибок необходимо, чтобы d = 2+ 1 + 1= 4. При d = 4 может быть также вариант, когда r = 3, s = 0. Если d = 5, то могут быть три варианта: r = s = 2; r= 3, s = 1; r = 4, s = 0. Если код только обнаруживает ошибки, то d = r + 1, т.е. r = d – 1. Если код только исправляет ошибки, то d = 2s+ 1, т.е. s= (d – 1) / 2. Геометрические модели позволяют просто строить и анализировать малоразрядные корректирующие коды. Однако при длине кода n > 3 геометрической моделью пользоваться трудно, так как она должна быть многомерной. Поэтому для построения многоразрядных помехоустойчивых кодов используют различные правила и методики, рассматриваемые далее. 4.6. КОДЫ С ОБНАРУЖЕНИЕМ ОШИБОК Особенность этих кодов состоит в том, что кодовые комбинации, входящие в их состав, отличаются друг от друга не менее чем на d = 2.Коды с обнаружением ошибок можно разбить на две группы: 1. Коды, построенные путём уменьшения числа используемых комбинаций. 2. Коды, в которых используются все кодовые комбинации, но к каждой из них добавляются по определённому правилу контрольные разряды. 4.6.1. Коды, построенные путём уменьшения числа используемых комбинаций Для построения этих кодов используется n-разрядный двоичный код на все сочетания. Из всех кодовых комбинаций формируется массив разрешённых комбинаций, обладающих некоторым общим признаком. Рассмотрим примеры построения кодов этой группы. 4.6.1.1. Код с постоянным весом Кодовые комбинации этого кода имеют постоянный вес, то есть имеют равное число единиц. Общее число кодовых комбинаций в двоичном коде с постоянным весом где l – число единиц в слове длиной п. Наиболее употребительными являются пятиразрядный код с двумя единицами (N=С52=10)и семиразрядный код с тремя единицами (N=С73=35). Примеры этих кодов представлены в табл. 4.9. Таблица 4.9 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
