ТОК Лекции. Конспект лекций Самара Самарский государственный технический университет 2011
 Скачать 6.93 Mb. Скачать 6.93 Mb.
|
Частотное разделение сигналов – разделение сигналов, при котором каждый сигнал занимает свой частотный интервал, не занятый другими сигналами.Частотно-временное разделение сигналов – разделение сигналов, при котором каждая позиция временного разделения уплотняется несколькими частотными каналами. КОНТРОЛЬНЫЕ ВОПРОСЫ
4. КОДЫ В ТЕЛЕМЕХАНИКЕ Кодирование нашло широкое применение во многих областях современных систем связи и передачи данных, в том числе в телемеханике. Оно дополняется кодоимпульсным способом передачи сообщений, который обеспечивает удобную реализацию и защиту передаваемой информации от помех. 4.1. КОД И ЕГО ХАРАКТЕРИСТИКИ Кодирование – преобразование дискретного сообщения в дискретный сигнал, осуществляемое по определенному правилу. В телемеханике сообщения носят либо дискретный характер, например, команды телеуправления, либо непрерывное сообщение, например сообщение ТИ, предварительно дискретизируется (квантуется по времени). Обратный процесс – декодирование – это восстановление дискретного сообщения по сигналу на выходе дискретного канала, осуществляемое с учетом правила кодирования. Код – совокупность условных сигналов, обозначающих дискретные сообщения. Кодовая последовательность (комбинация) – представление дискретного сигнала. Код имеет следующие основные характеристики: 1.Основание кода (q) или число признаков, равное числу отличающихся друг от друга символов (признаков). Наибольшее распространение получили коды с q=2, называемые бинарными, двоичными. Они характеризуются наиболее высокой надежностью передачи признаков по сравнению с кодами, имеющими другие основания. 2. Длина кодовой комбинации (n), называемая также разрядностью кода или длиной слова, она равна числу символов (элементарных сигналов) в кодовой комбинации. Код называется равномерным, если все кодовые комбинации одинаковы по длине, и неравномерным, если величина n в коде непостоянна. В телемеханике обычно используют равномерные коды, в которых легко контролировать длину слова для повышения помехоустойчивости. 3. Число кодовых комбинаций (N) в коде, каждая из которых может передавать свое отдельное сообщение. Этот показатель называют также объемом кода. Максимальный объем кода N=qn . 4.Вес кода (w), под которым понимают число единиц в кодовой комбинации. 4.2. КЛАССИФИКАЦИЯ КОДОВ Общая классификация кодов производится по нескольким критериям. 1. По области применения различают: 1.1. Телемеханические коды. 1.2. Телеграфный код. 1.3. Коды цифровой техники (ЭВМ). 1.4. Специальные (морской, коммерческий, дипломатический, военный) коды. Последние три из перечисленных кодов достаточно хорошо характеризуются своими названиями, в рамках настоящей дисциплины далее подробно будут рассмотрены только телемеханические коды. 2. В зависимости от цели, достигаемой кодированием, различают: 2.1. Первичные коды представления данных, или первичные коды. Они используются для отображения данных, получаемых либо при исходном кодировании дискретных величин, либо при преобразовании непрерывной величины в дискретную. 2.2. Оптимальные (эффективные) коды. Это коды, в которых принятый критерий оптимальности имеет экстремальное значение. Наиболее распространёнными являются коды с минимальным числом разрядов, приходящихся на одно сообщение. Передача таких кодов в последовательной форме, например, по линии связи, производится за минимальное время. При такой передаче недопустимы искажения, так как любое искажение приводит к необнаруживаемой ошибке воспроизведения исходной информации, поэтому такие коды в телемеханике не используются. 2.3. Помехозащищённые (корректирующие) коды. Это коды, которые способны либо обнаружить, либо обнаружить и исправить искажение, возникшее, например, при передаче. Благодаря этому свойству корректирующие коды широко применяются в телемеханике и в технике передачи данных. 3. По закономерностям кодообразования: 3.1. Числовые (взвешенные) коды, называемые еще цифровыми, имеют кодовые комбинации, образующие ряд возрастающих по весу чисел, определяемый системой счисления. Они применяются для кодирования количественной информации (например, при телеизмерении) 3.2. Нечисловые (не взвешенные) коды не имеют систем счисления и не образуют ряда возрастающих по весу кодовых комбинаций. Нечисловые коды применяются при передаче качественной информации (например, команды телеуправления). Они разделяются на следующие виды: 3.2.1. Комбинаторные, построенные по законам теории соединений. 3.2.2. Защищённые, имеющие специальные закономерности построения. 4.3. ОБЩИЕ СПОСОБЫ ПРЕДСТАВЛЕНИЯ КОДОВ Для представления кодов применяются следующие основные способы:
1. Таблица кодовых комбинаций представляет собой таблицу, в которой записаны все комбинации кода вместе с соответствующими числами. Например, таблица комбинаций трёхразрядного двоичного нормального (натурального) кода имеет следующий вид (табл. 4.1). Таблица 4.1 Таблица комбинаций трёхразрядного двоичного натурального кода
2. Кодовое дерево представляет собой графическое отображение множества кодовых комбинаций (рис. 4.1). 3. Геометрическая модель является другим способом графического представления кодов. Любой n-мерный двоичный код представляется n-мерным кубом, в котором каждая вершина отображает кодовую комбинацию, а длина ребра куба соответствует одной единице. В таком кубе расстояние между вершинами (кодовыми комбинациями) измеряются минимальным количеством ребер между ними (рис. 4.2). 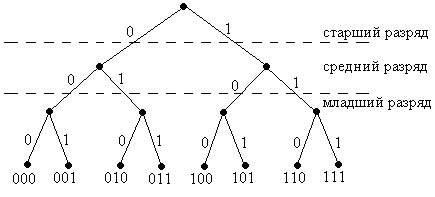 Рис. 4.1. Кодовое дерево трёхразрядного двоичного натурального кода 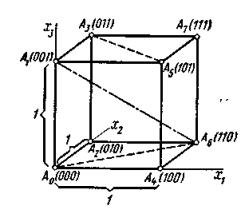 Рис. 4.2. Геометрическая модель трёхразрядного двоичного натурального кода Выбор способа представления определяется целью анализа или применения кода. 4.4. ПЕРВИЧНЫЕ КОДЫ В системах телемеханики в качестве первичных используются следующие коды. 4.4.1. Единичный (унитарный, числоимпульсный) код Кодовые комбинации его отличаются друг от друга числом единиц. Код неравномерный, но может быть сделан равномерным путем добавления соответствующего количества нулей слева до 10. Этот код применяется в номеронабирателе телефона. Таблица кодовых комбинаций единичного кода представлена в табл. 4.2. Таблица 4.2 Таблица комбинаций единичного кода
4.4.2. Единичный позиционный код Кодовые комбинации отличаются друг от друга положением единицы в их разряде. Таблица комбинаций единичного позиционного кода представлена в табл. 4.3. Таблица 4.3 Таблица комбинаций единичного позиционного кода
Единичный позиционный код является равномерным. 4.4.3. Единично-десятичный код Каждый разряд десятичного числа записывается в единичном коде, при этом между символами единично-десятичного кода, отображающими один разряд десятичного кода, ставится пробел. Этот код неравномерный, но может быть преобразован в равномерный. Для этого каждый разряд десятичного числа кодируется равномерным единичным кодом. Примеры единично-десятичного кода представлена в табл. 4.4. Таблица 4.4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
