Шпоры РХТУ им. Менделеева все формулы по ОНХ. химия онх. Конспект лекций, задачи и упражнения

• Название: Конспект лекций, задачи и упражнения
• Анкор: Шпоры РХТУ им. Менделеева все формулы по ОНХ
• Дата: 17.04.2021
• Размер: 0.51 Mb.
• Имя файла: химия онх.docx
• Тип: Конспект; #195637
• страница: 6 из 10

3.4. Равновесие растворения и диссоциации малорастворимого электролита

 

Пример 1. Произведение растворимости Ag₂S при 298,15 К составляет 6,9010^-50. Определить:

а) растворимость Ag₂S в воде (моль/л, г/л);

б) растворимость Ag₂S в 0,1 М растворе AgNO₃;

в) растворимость Ag₂S в 0,1 М растворе Na₂S;

г) в каком количестве воды растворяется 1 г Ag₂S;

д) G⁰ процесса растворения и диссоциации Ag₂S _(к).

 

Решение:

а) Пусть растворимость Ag₂S в воде составляет Р моль/л. В соответствии с уравнением растворения и диссоциации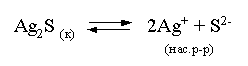



концентрации ионов составляют: [S^2–] = Р , [Ag⁺] = 2P. Подставляем эти величины в выражение для ПР:

ПР = [Ag⁺]² [S^2–] = (2P)²P = 4P³ = 6,9010^–50

 

и находим величину растворимости: Р = 2,5810^–17 моль/л. Для нахождения растворимости в г/л полученное значение следует умножить на молярную массу Ag₂S, получим 6,4010^–15 г/л.

 

б) Теперь Ag₂S растворяется в растворе, где уже есть ионы серебра с концентрацией 0,1 моль/л. Пусть растворимость Ag₂S в этом случае составляет P₁ моль/л. Концентрации ионов составят: [S^2–] = P₁; [Ag⁺] = 2P₁ + 0,1.

Подставляем эти величины в выражение для ПP:

 

(2P₁+0,1)²P₁  0,01 P₁ = 6,9010^-50.

 

Находим растворимость Ag₂S в 0,1 М растворе AgNO₃:

 

P₁ = 6,9010^–48 моль/л.

 

в) В этом случае Ag₂S растворяется в растворе, где уже есть анионы серы, их концентрация составляет 0,1 моль/л. Пусть растворимость Ag₂S в этом растворе составляет Р₂ моль/л; концентрации ионов составят: [S^2–]=P₂ +0,1; [Ag⁺] = 2P₂.

 

Подставляем эти величины в выражение для ПР:

 

ПР = (2P₂)² (P₂+0,1)  0,4 P₂² = 6,9010^–50.

 

Находим растворимость Ag₂S в 0,1 М растворе Na₂S:

 

Р₂ = 4,1510^–25 моль/л.

 

Как видно, в растворах с общим ионом растворимость Ag₂S меньше, чем в воде – наиболее резко упала растворимость в случае раствора AgNO₃.

 

г) В пункте а) была найдена растворимость Ag₂S в воде в г/л, она составила 6,4010^–15. Эта величина позволяет определить, в каком объеме воды растворяется 1 г Ag₂S:

 

6,4010^–15 г – в 1л

1 г – в Х л; откуда Х = 1,5610¹⁴ л.

 

д) Поскольку величина ПР представляет собой константу равновесия, то значение G⁰ процесса растворения и диссоциации Ag₂S легко вычисляется по известному соотношению:

 

G⁰ = – RT ln ПР = –8,31298,15ln 6,9010^–50 = 280,5 кДж.

 

Пример 2. По справочным данным определить значение растворимости СаF₂ при 298,15 К.

 

Решение. Первоначально находим значение ПР для CaF₂ по величине G⁰ процесса:

G⁰ = G⁰обрСа²⁺ (р-р, ст.с) + 2G⁰обр F^– (р-р, ст.с) – G⁰обрСаF₂ (к) =

= –552,8 + 2(–277,7) –(–1168,5) = 60,3 кДж.

G⁰ = – RTlnПР = –8,31298,15 ln ПР

Далее в соответствии с написанным выше уравнением растворения и диссоциации CaF₂ растворимость этого соединения численно равна концентрации иона кальция, а концентрация фторидного иона в 2 раза больше растворимости:

 

[Ca²⁺] = P; [F^–] = 2P; ПР = [Ca²⁺] [F^–] = P(2P)² = 4P³ = 2,6910^–11.

Отсюда растворимость равна: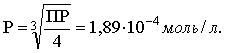

 



 

Пример 3. 0,1 г BaSO₄ промыты 500 мл воды. Определить возможный процент потерь осадка вследствие растворимости, считая, что промывные воды насыщены сульфатом бария. ПР BaSO₄ = 1,9510^–10.

 

Решение. Согласно уравнению:

ПР BaSO₄ = [Ba²⁺][SO₄^2–] = PP = P²,

 

где Р – растворимость BaSO₄ в воде.

Находим Р:

 

моль/л или

1,3910–5 моль/л  233,4 г/моль = 3,2610–3 г/л

 

Соответственно, в 500 мл насыщенного раствора будет находиться 1,6310^–3 г BaSO₄. Отсюда возможная потеря соли вследствие растворимости осадка составит

 

.

 

Пример 4. Смешали 1 л 0,01 М раствора Pb(NO₃)₂ и З л 0,1 М раствора КI. Выпадет ли осадок РbI₂, если ПР_PbJ2 = З,5610^–9. Считать объем окончательного раствора равным 4 л.

 

Решение. Для ответа на вопрос задачи следует вычислить произведение концентраций ионов Рb²⁺ и I^– в гипотетическом растворе после смешения
и сравнить его с величиной ПР. В исходных растворах концентрации ионов составляли соответственно:

 

[Pb²⁺] = 0,01; [I^–] = 0,1 моль/л.

 

После смешения они составят: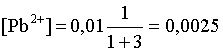

 

моль/л;

моль/л.

 

Произведение концентраций ионов в полученном растворе составит

 

ПК = [Pb²⁺][I^–]² = (0,0025)(0,075)²=1,4110^–5.

 

Как видно, ПК >ПР, следовательно осадок выпадет.

 

Пример 5. Массовая доля растворенного вещества в насыщенном при 298,15 К водном растворе CdS составляет 1,1910^–15. Определить ПР этого соединения, полагая, что плотность раствора равна 1 г/мл.

 

Решение. В 1 кг раствора (1 л раствора) находится 10001,1910^–15 = = 1,1910^–12 г CdS, что составляет 1,1910^–12 : M_CdS = 8,2610^–15 моль.

Согласно уравнению растворения и диссоциации CdS:

концентрации ионов в насыщенном растворе составят: [Cd²⁺] = [S^2–] = = 8,2610^–15 моль/л. Находим значение ПР:

ПР = [Cd²⁺][S^2–] = (8,2610^–15)² = 6,8210^–29.

3.5. Равновесие диссоциации воды, буферные растворы

 

Пример 1. Определить рН: а) 0,01М раствора HI; б) 0,01М раствора CsOH; в) 0,01М раствора СН₃СООН, К_дис = 1,7510^–5.

 

Решение: a) HI в водном растворе является сильным электролитом, поэтому: [HI] = [H⁺] =0,01 моль/л. Отсюда рН = – lg 0,01 = 2.

6) CsOH – сильный электролит, поэтому: [CsOH] = [OH^–] = 0,01 моль/л.

Отсюда рОН = – lg 0,01 = 2, а рН = 14 – 2 = 12.

в) CH₃COOH – слабый электролит в водном растворе, уравнение диссоциации:

 

Определим концентрацию ионов водорода: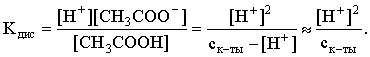

 



 



 

Затем находим рН раствора:

 

pH = – lg [H⁺] = –lg 4,1810^-4 = 3,38.

 

Пример 2. рН 0,1 М раствора слабого однокислотного основания равен 11. Найти константу и степень диссоциации этого основания.

 

Решение. Диссоциация слабого однокислотного основания описывается схемой:

Если рН раствора равен 11, то рОН =14–11=3; отсюда [OH^–]=110^–3 моль/л. В соответствии с уравнением диссоциации: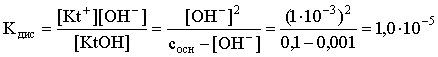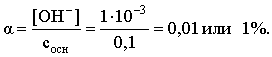

 



 



 

Пример З. Определить рН буферного раствора, полученного смешением 1 л 0,1 М раствора СН₃СООН и 2 л 0,01 М раствора CH₃COONa. Считать объем окончательного раствора равным З л. К_дис СН₃СООН = 1,7510^–5.

 

Решение. В водных растворах СН₃СООН и CH₃COONa реализуются следующие равновесия: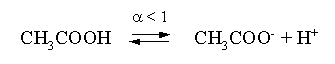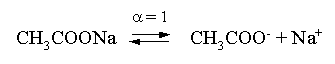





 

Диссоциация слабой кислоты подавлена диссоциацией соли, имеющей тот же анион, что и кислота. В силу этого:

 

[CH₃COO^-] = [CH₃COO^-]_к-ты + [CH₃COO^-]_соли  с_соли ;

[CH₃COOH]  с_к-ты .

 

Учитывая это, запишем для К_дис кислоты и [Н⁺]: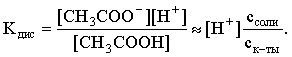

 



 

С учетом разбавления концентрации соли и кислоты составят:





 

Находим из константы диссоциации концентрацию ионов водорода и рН раствора: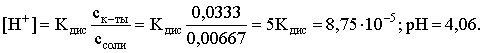

 



 

Пример 4. Какой объем 0,5 М раствора ацетата натрия следует прилить к 1 л 0,1 М раствора СН₃СООН, чтобы рН полученного буферного раствора составил 5. Считать, что объем полученного раствора равен сумме объемов сливаемых растворов; К_дис СH₃COOH =1,7510^–5.

 

Решение. В соответствии с формулой (3.21) для кислого буферного раствора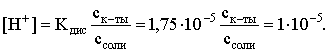



Отсюда:

 

Пусть для получения требуемого раствора к 1 л 0,1 М раствора СН₃СООН следует прибавить Х л 0,5 М раствора CH₃COONa. Соответственно, тогда
в буферном растворе:

<sup>моль/л;

моль/л.</sup>

Подставляем эти величины в написанное выше соотношение: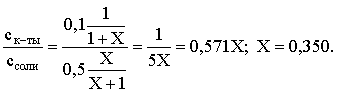



 

Таким образом, для получения раствора с требуемой величиной рН необходимо к 1 л 0,1 М раствора СН₃СООН добавить 350 мл 0,5 М раствора CH₃COONa.

 

Пример 5. На сколько единиц изменится рН раствора слабой одноосновной кислоты при его разбавлении в 10 раз ?

Решение. Константа диссоциации слабой одноосновной кислоты имеет вид (см. пример 1 этого раздела):

Имея в виду равенство констант диссоциации кислоты в растворах двух концентраций, запишем:

 

или

.

 

Логарифмируем это соотношение:

 

2 lg [H⁺]₁ = 1 + 2lg [H⁺]₂ .

 

Делим обе части уравнения на 2 и меняем знаки: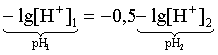

 



pH₁ = pH₂ – 0,5.

 

Следовательно, при разбавлении раствора слабой одноосновной кислоты в 10 раз рН раствора возрастает на 0,5.

 

Пример 6. Вычислить рН насыщенного раствора Mg(OH)₂. ПР Mg(OH)₂ = = 1,4710^–11.

 

Решение. В насыщенном растворе Mg(OH)₂ существует равновесие: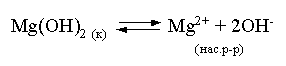



Пусть растворимость гидроксида магния в воде равна Р моль/л, тогда концентрации ионов в насыщенном растворе составят: [Mg²⁺] = P, [OH^–] = 2P.

Подставляем эти величины в выражение для ПР:

 

ПР = [Mg²⁺] [OH^–]² = P(2P)² = 4P³ = 1,4710^–11.

 

Находим рН насыщенного раствора гидроксида магния:

 

^; [OH^–] = 2P = 3,0810^–4.

pOH = –lg 3,0810^–4 = 3,51; pH = 14 – 3,51 = 10,49.

 

Пример 7. Определить рН, при котором начинается осаждение Fе(ОН)₃ из 0,1 М раствора FeCl₃. ПР Fe(OH)₃ = 6,4010^–40.

 

Решение. Пусть растворимость Fe(OH)₃ в 0,1 М растворе FeCl₃ составляет Р моль/л. Тогда в соответствии с уравнением растворения и диссоциации Fе(ОН)₃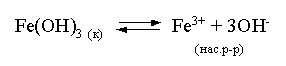



концентрации ионов в насыщенном растворе Fe(ОН)₃ составят: [OH^–]= 3P; [Fe³⁺] = 0,1 + P. Подставляем эти величины в выражение для ПР:

 

ПР Fe(OH)₃ = [Fe³⁺][OH^–]³ = (0,1+P)(3P)³  2,7P³ = 6,4010^–40;

 

находим концентрацию ионов ОН^– и рН начала выпадения Fе(ОН)₃ из 0,1 М раствора FeCl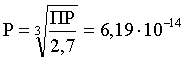₃

 

^; [OH^–] = 3P = 1,8610^–13.

pOH = –lg 1,8610^–13 = 12,7; pH = 14 – pOH = 1,3.

 

3.6. Гидролиз солей

 

Пример 1. Определить рН 0,3 М раствора NH₄Br, если константа диссоциации гидроксида аммония в водном растворе составляет 1,7110^–5.

 

Решение. Бромид аммония гидролизован по катиону в растворе:

Согласно соотношению (3.23):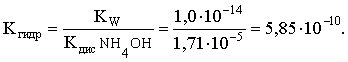

 



 

С другой стороны (соотношение 3.24):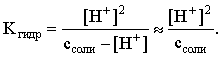

 



Из этих двух выражений и вычисляем рН 0,3 М раствора NH₄Br:

 



pH = – lg 1,3210^–5 = 4,88 .

 

Пример 2. Определить рН раствора и степень гидролиза соли в 0,1 М растворе Na₂S, если константы ступенчатой диссоциации H₂S составляют: К₁=9,7410^–8; К₂= 1,3610^–13.

 

Решение. Сульфид натрия – соль, гидролизованная по аниону. Поскольку сероводородная кислота двухосновна, гидролиз идет по двум ступеням. Выше было показано, что для практических расчетов достаточно принимать во внимание лишь первую ступень гидролиза. В нашем случае это следующий процесс:

Определяем константу гидролиза: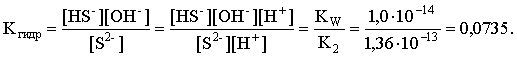

 



 

С другой стороны: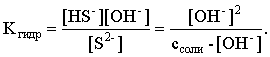



 

Решая полученное квадратное уравнение, находим рН раствора и степень гидролиза:

 

[ОН^–] = 0,0565 (второй корень уравнения отрицателен!)

рОН = – lg 0,0565 = 1,25; рН = 14 – 1,25 = 12,75;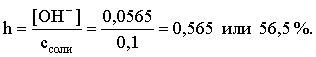