Шпоры РХТУ им. Менделеева все формулы по ОНХ. химия онх. Конспект лекций, задачи и упражнения

• Название: Конспект лекций, задачи и упражнения
• Анкор: Шпоры РХТУ им. Менделеева все формулы по ОНХ
• Дата: 17.04.2021
• Размер: 0.51 Mb.
• Имя файла: химия онх.docx
• Тип: Конспект; #195637
• страница: 5 из 10

3.1. Образование растворов, растворимость

 

Пример 1. Пользуясь справочными данными, определить давление паров над водой при 298,15 К.

 

Решение. Равновесие испарения воды

описывается соответствующей константой, численно равной давлению водяных паров (концентрация жидкой воды постоянна и равна 1!):

K_равн = P_H2O .

Находим величину G⁰ указанного процесса:



G⁰ = G⁰обр H₂O(г) – G⁰ обр H₂O(ж) = –228,6 – (–237,3) = 8,7 кДж .

 

Вычисляем давление паров воды:

 

G⁰ = – RTlnK_равн = –RTlnP_H2O;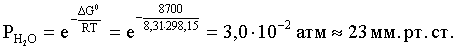

 



 

Пример 2. Пользуясь справочными данными, определить растворимость йода в воде при 298,15 К.

 

Решение. Для равновесия

константа равновесия равна:

 

K_равн = .

 

Определим G⁰ для указанного процесса:

 

G⁰ = G⁰обр I₂ (р-р, ст.с) – G⁰ обр I₂ (к) = G⁰ обр I₂ (р-р, ст.с) = 16 кДж .

 

Далее:

G⁰ = – RTlnK_равн = –RTln a _{I2 (нас.р-р)} = G⁰ обр I₂ (р-р, ст.с)

 

Как видно, растворимость йода в воде мала, поэтому активность можно уверенно считать равной концентрации (коэффициент активности равен единице). Таким образом, растворимость йода в воде при 298,15 К составляет 1,6·10^-3 моль/л или 0,40 г/л.

 

Пример 3. 44,8 л (н.у.) хлороводорода растворили в 300 мл воды. Определить моляльность полученного раствора и массовую долю НСl
в нем.

 

Решение. 44,8 л (н.у.) хлороводорода составляют 2 моль и имеют массу 2·36,5 = 73,0 г. Масса полученного раствора составляет (плотность воды 1,00 г/мл): 300 · 1 + 73,0 = 373,0 г.

Определяем массовую долю хлороводорода в растворе:

.

 

Наконец, находим моляльность полученного раствора:

 

2 моль НСl – 0,30 кг Н₂О

Х – 1,00 кг,

откуда Х = m_р-ра = 6,67 моль/кг.

Пример 4. Какой объем 3,00 мас.% раствора NaCl (плотность раствора 1,020 г/мл) и 12,00 мас.% раствора NaCl (плотность раствора 1,086 г/мл) необходимо смешать для приготовления 400 мл 7,50 мас.% раствора этого соединения с плотностью 1,053 г/мл?

 

Решение. Задача сводится к составлению двух материальных балансов – масса приготовляемого раствора равна сумме масс составляющих его растворов и масса растворенного вещества в приготовляемом растворе равна сумме масс этого вещества в двух исходных растворах. Необходимо помнить, что для объемов растворов это правило не выполняется! Пусть необходимый объем 3,00 мас.% раствора составляет Х мл, а объем 12,00 мас.% раствора – Y мл.

Первое уравнение:

1,020X + 1,086Y = 4001,053 = 421,2;

второе уравнение:

0,031,020X + 0,121,086Y = 0,075421,2 = 31,6

 

Решение этой системы уравнений приводит к результату: Х = 205,4 мл, Y= 194,8мл.

 

Пример 5. Сколько граммов кристаллогидрата Na₂SO₄10H₂O и мл воды необходимо для приготовления 400 мл 15 мас.% раствора Na₂SO₄ с плотностью 1,142 г/мл. Определить молярность, моляльность, титр приготовленного раствора, а также мольную долю Na₂SO₄ в растворе.

 

Решение. Определим содержание Na₂SO₄ в приготовляемом растворе:

 

m_Na2SO4 = m_р-ра  0,15 = 400  1,142  0,15 = 68,5 г .

Молярная масса Na₂SO₄ составляет 142 г/моль, a Na₂SO₄10H₂O – 322 г/моль. Соответственно, 68,5 г Na₂SO₄ содержатся в 68,5322/142 = 155,3 г кристаллогидрата. Наконец, находим массу (объем) воды, необходимой для приготовления раствора:

 

m_H2O = V_H2O = m _р-ра – m _кр-та = 400  1,142 – 155,3 = 301,5 г или 301,5 мл.

 

Теперь решаем отдельную задачу о нахождении молярности, моляльности, титра и мольной доли соли в 15 мас.% растворе Na₂SO₄. Поскольку
в определении молярности и титра задействованы литр и миллилитр, целесообразно отталкиваться от объема раствора, равного 1 л. Итак пусть имеется 1 л 15 мас.% раствора Na₂SO₄ с плотностью 1,142 г/мл. Находим массу растворенной в нем соли и переводим в моли:

 

m_Na2SO4 в 1 л р-ра = 1000  1,142  0,15 = 171,3 г

 

 

Тут же легко находится титр: Т = 171,3 / 1000 = 0,1713 .

Теперь определим массу воды в 1 л раствора:

 

m_H2O = 1142 - 171,3 = 970,7 г

 

и вычисляем моляльность:

.

В 1 л раствора находится 1,21 моль соли и 970,7/18 = 53,9 моль воды, отсюда мольная доля соли составляет:

мольная доля .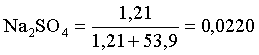

Пример 6. Сколько мл 20 мас.% раствора NaOH необходимо прилить к 500 мл 5 мас.% раствора того же соединения для получения 2М раствора NaOH. Плотности растворов равны соответственно 1,219; 1,054 и 1,080 г/мл.

 

Решение. Решение задачи сводится к нахождению числа молей NaOH в приготовляемом растворе и его объема (в литрах).

Пусть необходимо прилить Х мл 20 мас.% раствора. Определим число молей (количество вещества) NaOH в двух сливаемых растворах: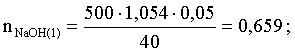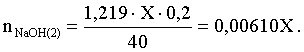

 





 

Объем окончательного раствора находим через его массу и плотность:

 

m_р-ра = m_р-ра(1) + m_р-ра(2) = 5001,054 + Х1,219 = 527 + 1,219Х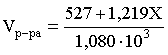



 

Согласно условию, число молей NaOH, отнесенное к объему раствора в литрах, равняется двум: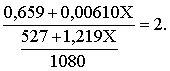

 



 

Решение этого уравнения и дает ответ – необходимо прилить 82,5 мл
20 мас.% раствора.

 

Пример 7. Раствор имеет мольное отношение NaOH : H₂O = 1 : 100. Определить концентрацию этого раствора в мас.% и его моляльность.

Решение. Раствор содержит 1 моль NaOH и 100 моль Н₂O, что составляет 40 г и 10018 = 1800 г соответственно. Находим моляльность:

 

1 моль NaOH – 1,8 кг Н₂О

Х – 1 кг Н₂О, откуда Х = m = 0,556.

 

Масса раствора составляет 40 + 1800 = 1840 г, а его концентрация

^{мас.% .}

 

3.2. Равновесие диссоциации электролитов

 

Пример 1. Константа диссоциации муравьиной кислоты 1,7010^–4. Найти концентрацию ионов водорода и степень диссоциации кислоты в ее 1 М растворе.

 

Решение. В соответствии с уравнением диссоциации кислоты:

записываем выражение для константы диссоциации:

 

К_дис = ^.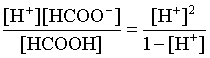

 

Концентрация ионов водорода существенно меньше единицы и ею можно пренебречь. Находим концентрацию ионов водорода:

 

.

 

Наконец, определяем степень диссоциации кислоты: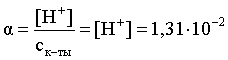

или 1,31 %.

Пример 2. Степень диссоциации слабой одноосновной кислоты в 0,1 М растворе составляет 0,1 %. Найти концентрацию ионов водорода в ее 1 М растворе.

 

Решение. Для нахождения константы диссоциации кислоты воспользуемся соотношением

К_дис = .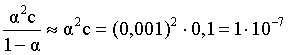

 

В соответствии с уравнением диссоциации кислоты

константа диссоциации связана с концентрацией ионов водорода следующим образом:

К_дис =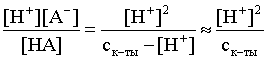

 

Определяем концентрацию ионов водорода в 1 М растворе:

 

^{моль/л .}

 

Пример 3. В 1 л 0,1 М раствора уксусной кислоты растворили 4,48 л (н.у.) хлороводорода. Как изменилась при этом степень диссоциации уксусной кислоты? Принять объем окончательного раствора равным 1 л, константа диссоциации уксусной кислоты составляет 1,7510^–5.

 

Решение. Определим степень диссоциации уксусной кислоты в исходном растворе: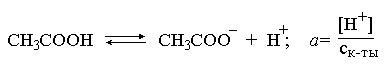



 

К_дис =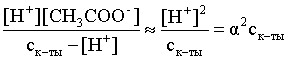

 

.

 

В соответствии с уравнением диссоциации появление в растворе сильной хлороводородной кислоты приведет к резкому смещению равновесия диссоциации уксусной кислоты влево. Пусть концентрация ионов водорода, образующихся за счет собственной диссоциации уксусной кислоты равна Х моль/л, такова же концентрация и ацетат-анионов; общая концентрация ионов водорода в растворе составит (X + 0,2) моль/л (4,48 л хлороводорода составляют 0,2 моль). Подставляем эти величины в выражение для константы диссоциации и находим X:

 

К_дис = .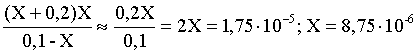

 

Определяем степень диссоциации уксусной кислоты в окончательном растворе: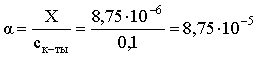

.

 

Таким образом, введение в раствор 0,2 моль хлороводорода привело к уменьшению степени диссоциации уксусной кислоты в: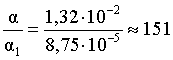

раз.

 

Пример 4. Константы ступенчатой диссоциации сероводородной кислоты составляют 9,7410^–8, 1,3610^–13. Найти концентрации ионов Н⁺, HS^– и S^2–
в 0,01 М растворе этой кислоты.

Решение. В соответствии с уравнением диссоциации H₂S по первой ступени

определяем концентрацию ионов Н⁺ и HS^– :

 

К_дис(1) = ;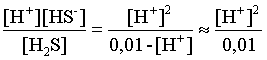

 



 

Диссоциация по второй ступени

протекает в значительно меньшей степени за счет подавления ее продуктами диссоциации по первой ступени и большей трудности отрыва протона от аниона по сравнению с нейтральной молекулой. Пусть концентрация анионов серы в растворе равна Х моль/л, концентрация ионов водорода составит (X + 3,1210^–5) моль/л, а концентрация ионов HS^– – (3,1210^–5 – X) моль/л. Подставляем эти величины в выражение для второй константы диссоциации:

 

К_дис(2) = .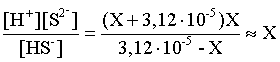

 

Таким образом, концентрация аниона серы практически равна значению второй константы диссоциации кислоты.

 

 

 

3.3. Шкала термодинамических функций образования ионов в водных растворах

 

Пример 1. На основе справочных данных определить вторую константу диссоциации ортофосфорной кислоты при 298,15 К.

 

Решение. Второй ступени диссоциации ортофосфорной кислоты соответствует процесс:

Находим стандартную энергию Гиббса этого процесса:

 

G⁰=G⁰_обр H⁺(р-р, ст.с) + G⁰_обр HPO₄^2-(р-р, ст.с, гип.недис) –

– G⁰_обр H₂PO₄^- (р-р, ст.с, гип.недис) = 0 + (–1083,2) – (–1124,3) = 41,1 кДж .

 

Затем определяем константу диссоциации:

 

G⁰ = –RTlnK_равн = –RTlnK_дис(2)

 

К_дис(2) = .

 

Пример 2. Стандартная энтальпия образования NaCl (к) равна –411,1 кДж/моль, энтальпия растворения этого соединения в воде с образованием бесконечно разбавленного раствора равна 3,6 кДж/моль, а стандартная энтальпия образования аниона хлора в водном растворе составляет –167,1 кДж/моль. Определить стандартную энтальпию образования иона Na⁺ .

 

Решение. Ключом к нахождению искомой величины является положение, что стандартная энтальпия образования NaCl в растворе равна сумме стандартных энтальпий образования ионов Na⁺ и Сl^– в растворе. Первая же величина, в свою очередь, равна сумме стандартных энтальпий образования NaCl (к) и энтальпии его растворения с образованием бесконечно разбавленного раствора. Таким образом:

 

H⁰_обр NaCl (р-р, ст.с) = H⁰_обр Na⁺ (р-р, ст.с) + H⁰_обр Cl^- (р-р, ст.с) =
= H⁰_обр NaCl (к) + H⁰_раств;

H⁰_обр Na⁺ (р-р, ст.с) = H⁰_обр NaCl (к) + H⁰_раств – H⁰_обр Cl^- (р-р, ст.с) =

= –411,1 + 3,6 – (–167,1) = –240,4 кДж/моль .

 

Пример 3. По следующим данным:

 

H⁰_обр NaCl (р-р, ст.с) = –407,5 кДж/моль = H⁰₁;

H⁰_обр KCl (р-р, ст.с) = –419,4 кДж/моль = H⁰₂;

H⁰_обр NaBr (р-р, ст.с) = –361,8 кДж/моль = H⁰₃;

H⁰_обр NaI (р-р, ст.с) = –295,6 кДж/моль = H⁰₄ .

 

определить H⁰_обрKBr (р-р, ст.с); H⁰_обрKI (р-р, ст.с) .

 

Решение. Поскольку стандартные энтальпии образования электролитов в растворе тождественно равны сумме стандартных энтальпий образования составляющих их ионов, можно записать:

 

H⁰_обрKCl (р-р, ст.с) – H⁰_обрNaCl (р-р, ст.с) = H⁰_обрK⁺ (р-р, ст.с) +

+ H⁰_обрCl^– (р-р, ст.с) – H⁰_обрNa⁺ (р-р, ст.с) – H⁰_обрCl^– (р-р, ст.с) =

= H⁰_обрK⁺ (р-р, ст.с) – H⁰_обрNa⁺ (р-р, ст.с)

 

Складываем эту величину c H⁰_обрNaBr (p-p, ст.с) и получаем:

 

H⁰_обрK⁺ (р-р, ст.с) – H⁰_обрNa⁺ (р-р, ст.с) + H⁰_обрNaBr (р-р, ст.с) =

= H⁰_обрK⁺ (р-р, ст.с) – H⁰_обрNa⁺ (р-р, ст.с) + H⁰_обрNa⁺ (р-р, ст.с) +

+ H⁰_обрBr^– (р-р, ст.с) = H⁰_обрKBr (р-р, ст.с)

 

Находим одну из искомых величин:

 

H⁰_обрKBr (р-р, ст.с) = H⁰₂ – H⁰₁ + H⁰₃ = –419,4 – (–407,5) + (–361,8) =

= – 373,7 кДж/моль.

 

Аналогично определяем H⁰_обрKI (р-р, ст.с):

 

H⁰_обрKCl (р-р, ст.с) – H⁰_обрNaCl (р-р, ст.с) + H⁰_обрNaI (р-р, ст.с) =

= H⁰_обрK⁺ (р-р, ст.с) – H⁰_обрNa⁺ (р-р, ст.с) + H⁰_обрNa⁺ (р-р, ст.с) +

+ H⁰_обрI^–(р-р, ст.с) = H⁰_обрKI (р-р, ст.с) = H⁰₂ – H⁰₁ + H⁰₄ =

= –419,4 – (–407,5) + (–295,6) = – 307,5 кДж/моль.