твмс. ТВМС. Теор. и практ. реш. тип. задач к.р.(23.09.20). Контрольная работа выполняется и оформляется при соблюдении следующих правил
 Скачать 2.47 Mb.
|
|
5. Теорема сложения вероятностей совместных событий При решении многих задач требуется найти вероятность суммы двух или нескольких совместных событий, т.е. вероятность появления хотя бы одного (любого) из них. В этом случае применяется следующая теорема. Теорема 3. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения: Р(А + В) = Р(А) + Р(В) − Р(АВ). (17) Заметим, что если события А и В независимы, то Р(АВ) = Р(А)·Р(В)и таким образом для независимых событий: Р(А + В) = Р(А) + Р(В) – Р(А)  Р(В). (18)Если события А и В зависимы, то Р(АВ) = Р(А) · Р(B/A) = Р(В) · P(A/B) и, таким образом, для зависимых событий Р(А + В) = Р(А) + Р(В) – Р(А) · Р(B/A) = Р(А) + Р(В) – Р(В) · P(A/B). (19) Если события А и В несовместные, то их произведение АВ=U (невозможное событие) и, следовательно, Р(АВ) = Р(U) = 0. Поэтому в случае несовместных событий имеем: Р(А + В) = Р(А) + Р(В), т.е. имеет место теорема сложения (9) для вероятности суммы несовместных событий. 6. Вероятность наступления хотя бы одного события Пусть в результате испытания может появиться n независимых событий, либо некоторые из них (в частности, только одно или ни одного), причем вероятности каждого из событий известны. Пусть требуется найти вероятность того, что наступит хотя бы одно из этих событий. Теорема 4. Вероятность наступления хотя бы одного из  независимых событий А1, A2,…,An равна разности между единицей и произведением вероятностей противоположных событий  Р(А) = 1 −  (20)Здесь  — вероятности противоположных событий;  В частности, когда события А1, A2,…,Anравновероятны, т.е.   то Р(А) = 1 – qn. (21) Пример 2. Вероятность рентабельной работы в течение года трех независимо работающих предприятий соответственно равна 0,5; 0,6; и 0,9. Найти вероятность того, что в течение года рентабельными будут: а) все три предприятия, б) только два предприятия. Решение. Обозначим события: А1 — первое предприятие в течение года работает рентабельно, А2 — второе предприятие в течение года работает рентабельно, А3 — третье предприятие в течение года работает рентабельно,  — первое предприятие работает нерентабельно,  — второе предприятие работает нерентабельно,  — третье предприятие работает нерентабельно.а) Вероятности противоположных событий — каждое из предприятий работает нерентабельно — согласно (12) соответственно равны:  Событие А — все три предприятия в течение года работают рентабельно согласно определению произведения событий, равно  и, следовательно, вероятность того, что в течение года все три предприятия будут работать рентабельно, равна Р(А)= По условию, предприятия работают независимо, согласно теоремы умножения вероятностей для независимых событий в силу (16) находим: Р(А)=Р(А1) · Р(А2) · Р(А3) = 0,5 · 0,6 · 0,9 = 0,27. б) Событие В — только два предприятия из трех в течение года будут работать рентабельно — будет осуществлено, если произойдет любое из следующих трех несовместных событий:  — первое и второе предприятия работают рентабельно, третье предприятие работает нерентабельно;  — первое и третье предприятия работают рентабельно, второе — нерентабельно;  — второе и третье предприятия работают рентабельно, первое — нерентабельно.Согласно определению суммы несовместных событий, событие В представим в виде:  По теореме сложения вероятностей несовместных событий (10) имеем:  Так как события А1, A2,…,A3 и, соответственно,  независимы, то по теореме умножения вероятностей для независимых событий в силу (16) находим: = 0,5 · 0,6 · 0,1 + 0,5 · 0,4 · 0,9 + 0,5 · 0,6 · 0,9 = 0,48. Ответ. а) Вероятность рентабельной работы всех трех предприятий в течение года равно 0,27. б) Вероятность рентабельной работы только двух предприятий равна 0,48. Пример 3. Экзаменационный билет содержит 3 вопроса. Для каждого вопроса предлагается 4 различных ответа, из которых только один является правильным. Для сдачи экзамена требуется правильно ответить на все три вопроса. Какова вероятность сдачи экзамена при случайном выборе ответов на вопросы экзаменационного билета? Решение. Обозначим события: А — экзамен будет сдан, А1  — правильный ответ на первый вопрос билета, А2 — на второй вопрос, А3 — на третий вопрос.Очевидно,  т.е. совместное осуществление трех событий, состоящих в том, что даны правильные ответы на все три вопроса билета.По условию для каждого вопроса предлагается 4 разных ответа, из которых только один является правильным. Следовательно, при случайном выборе ответа на каждый из вопросов общее число равновозможных исходов выбора ответа равно n = 4, из них только один исход (m = 1) является благоприятствующим правильному ответу. Таким образом, согласно (1) и условию задачи   Учитывая, что события А1, A2,…,A3 независимые, по теореме умножения вероятностей для независимых событий (16) получаем:  Ответ. Вероятность сдачи экзамена равна 0,015. Пример 4. Из 10 экзаменационных билетов 3 билета содержат простые вопросы. 4 студента по очереди берут билеты. Найти вероятность того, что хотя бы одному из студентов достанется билет с простым вопросом. Решение. Число способов четырем студентам выбрать 4 из 10 билетов равно С  — числу сочетаний из 10 по 4. Согласно (7) имеем: По условию, из 10 экзаменационных билетов только 3 билета содержат простые вопросы и, следовательно, 7 билетов не содержат простых вопросов. Число способов четырем студентам взять 4 билета, в каждом из которых не будет простого вопроса, равно  числу сочетаний из 7 по 4. Согласно (7) имеем: Обозначим события: А — хотя бы одному из студентов достанется билет с простым вопросом,  — никому из студентов не достанется билет с простым вопросом.Найдем вероятность  того, что никому из студентов не достанется билет с простым вопросом. Из (1) и (8) получаем: Искомая вероятность того, что хотя бы одному из студентов достанется билет с простым вопросом, согласно (12) равна:  Ответ. Вероятность того, что хотя бы одному из студентов достанется билет с простым вопросом равна 0,833. Пример 5. Три стрелка независимо друг от друга стреляют по цели, делая по одному выстрелу. Вероятность попадания в цель первого стрелка равна 0,7, для второго — 0,6, для третьего — 0,95. Найти вероятность того, что: а) все три стрелка попадут в цель; б) все три стрелка промахнутся; в) хотя бы один стрелок попадет в цель. Решение. Обозначим события: A1 — первый стрелок попадет в цель; A2 — второй стрелок попадет в цель; A3 — третий стрелок попадет в цель;  промах первого стрелка;  промах второго стрелка;  промах третьего стрелка.а) Рассмотрим событие А, состоящее в том, что все три стрелки попали в цель. По определению произведения событий по теореме умножения вероятностей независимых событий (16): б) Рассмотрим событие  состоящее в том, что все три стрелка промахнутся. По определению произведения событий  по теореме умножения вероятностей независимых событий (16): Так как согласно (12) 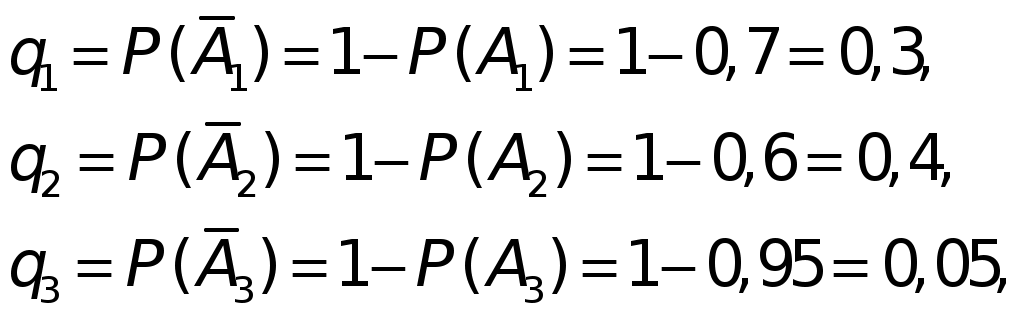 то получаем:  в) Вычислим теперь вероятность события В, состоящего в том, что хотя бы один стрелок попадет в цель. Из (20) имеем:  Ответ. а) Вероятность того, что все три стрелка попадут в цель равна 0,4. б) Вероятность того, что все три стрелка промахнутся равна 0,006. в) Вероятность того, что хотя бы один стрелок попадет в цель равна 0,994. 7. Формула полной вероятности. Формула Байеса Пусть событие А может наблюдаться при условии наступления одного из событий  образующих полную группу попарно несовместных событий. Вероятности P(Ei),  заданы. События Ei иногда называют гипотезами. Требуется вычислить вероятность наступления события А.Искомая вероятность определяется по формуле, называемой формулой полной вероятности: 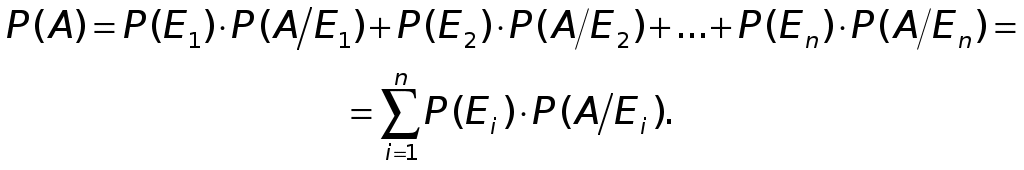 (22)Пусть в выше сформулированных условиях в результате проведения испытания наступило событие А. Требуется переоценить вероятности гипотез, т.е. определить вероятность  события Ek  при условии, что событие А наступило.Искомая вероятность определяется формулой Байеса: 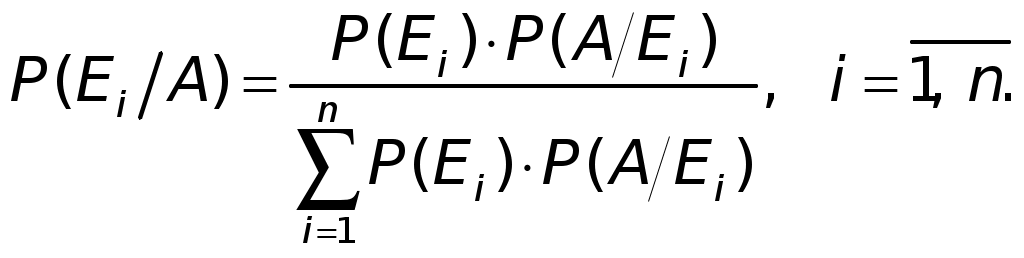 (23)Пример 6. На склад готовой продукции поступили изделия двух заводов, в том числе 40% с первого завода и 60% со второго. Среди изделий первого завода брак в среднем составляет 10%, из изделий второго завода 75% не имеют брака. Найти вероятность того, что взятое наугад со склада изделие не окажется бракованным. Решение. Обозначим: событие А — взятое изделие не окажется бракованным. Рассмотрим гипотезы:  взятое изделие изготовлено на первом заводе,  взятое изделие изготовлено на втором заводе.Так как на складе находится 40% изделий первого завода и 60% — второго, то вероятности гипотез равны:   Вычислим условные вероятности  и  Так как среди изделий первого завода брак в среднем составляет 10%, то 90% изделий первого завода не имеют брака. Следовательно, вероятность  того, что взятая на складе деталь не окажется бракованной и при этом она изготовлена на первом заводе равна  Так как 75% изделий второго завода не имеют брака, то вероятность того, что взятая на складе деталь не окажется бракованной и при этом она изготовлена на втором заводе равна  Теперь по формуле полной вероятности (22) получаем:  Ответ. Вероятность того, что взятое наугад со склада изделие не окажется бракованным, равна 0,81. Пример 7. Два оператора набили по равному комплекту перфокарт. Вероятность ошибки первого оператора равна 0,15, второго — 0,18. При проверке перфокарт обнаружена ошибка. Какова вероятность того, что обнаруженная ошибка допущена первым оператором? Решение. Рассмотрим гипотезы: E1 — проверенная карта набита первым оператором, E2 — карта набита вторым оператором. Так как по условию операторы набили равное количество перфокарт, то  Обозначим: А — событие, состоящее в том, что при проверке перфокарт будет обнаружена ошибка. Вероятность того, что ошибку может допустить первый оператор является условной и заданной  Аналогично,  — условная вероятность ошибки второго оператора.По формуле Байеса (23), используя дополнительную информацию о том, что при проверке перфокарт обнаружена ошибка, пересчитаем вероятность 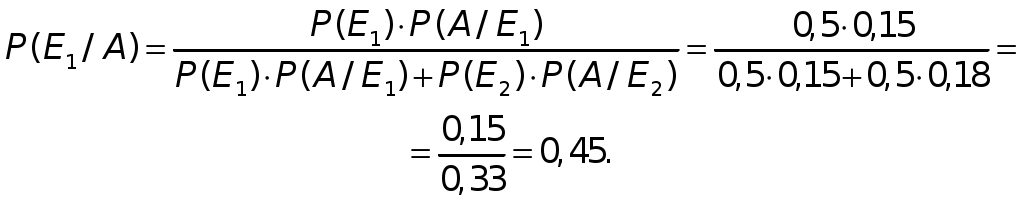и вычислим вероятность того, что ошибка была допущена первым оператором   |