твмс. ТВМС. Теор. и практ. реш. тип. задач к.р.(23.09.20). Контрольная работа выполняется и оформляется при соблюдении следующих правил

• Название: Контрольная работа выполняется и оформляется при соблюдении следующих правил
• Дата: 21.12.2022
• Размер: 2.47 Mb.
• Имя файла: ТВМС. Теор. и практ. реш. тип. задач к.р.(23.09.20).doc
• Тип: Контрольная работа; #857186
• страница: 1 из 9

ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Теория и практика решения типовых задач контрольных работ

Введение

Учебный процесс по изучению математики завершается формированием математического мышления студентов на основе представлений о математике как о символической картине мира, описывающей многообразие явлений окружающей действительности на языке символов с помощью математических моделей. Следует обратить внимание на три новые для студента фундаментальные понятия: опыт, случайное событие, вероятность случайного события. Изучение вероятностных моделей развивает новый образ математического мышления — вероятностное мышление.

Математические методы и модели ориентируют студентов на получение элементарных навыков современного научного исследования процессов, изучаемых в специальных дисциплинах, а также качественных и количественных признаков изделий, изготавливаемых по инновационным технологиям и предназначенным для реализации в условиях рыночных конкурентных отношений.

При выполнении контрольных работ рекомендуется предварительное тщательное и в достаточном объеме изучение теоретического базисного учебного материала — основных понятий и теорем, на которых построены методы типовых решений задач, проконсультироваться у преподавателя, затем рассмотреть типовые решения задач и приступить к выполнению индивидуального задания.

Контрольная работа выполняется и оформляется при соблюдении следующих правил.

1. Контрольная работа набирается в WORD.

2. На обложке записывают:

• Номер контрольной работы.

• Название темы и дисциплины.

• Название кафедры.

• Название факультета.

• Фамилия, имя, отчество студента.

• Учебный шифр студента.

3. Номер варианта выбирается по последней цифре учебного шифра студента, проставленного в зачетной книжке.

4. Задачи располагаются в порядке, указанном в задании на контрольную работу под своими номерами.

5. Условие задачи полностью, без сокращений переписывается из задания на контрольную работу. После условия задачи отдельной строкой записывается слово «Решение», а далее последовательно по пунктам с подробными объяснениями, без сокращенных слов, аккуратно и четко, со ссылками на необходимые теоремы, утверждения, определения понятий и формулы излагается ход решения.

6.Выполненную контрольную работу необходимо предъявить преподавателю для проверки. Преподаватель делает замечания к решениям задач, указывает на недостатки оформления и выносит заключение «Контрольная работа № ... допущена к зачету» или «Контрольная работа № ... не допущена к зачету. Зачет по контрольной работе студент получает после собеседования с преподавателем по содержанию контрольной работы и ответов на вопросы к зачету.

.

Теория и практика решения типовых задач
Задача 1. Случайные события. Основные теоремы и формулы

[1, С, 1.1–1.3, 2.1–2.4, 3.1–3.4], [2, 19.1–19.5], [5, гл. 1, § 1, гл. 2, § 1–4, гл. 3, § 1],

[6, разд. 1, гл. 1, § 1.1–1.14], [7, разд. 1, гл. 1–4], [9, 6.1.1–6.1.4, 6.2]

1. Вероятность случайного события

Случайным событием (или просто событием) называется любой результат испытания, о котором заранее в силу неизвестных причин нельзя сказать определенно, что он может быть либо получен, либо не получен.

Под испытанием (опытом, экспериментом) понимается планируемое выполнение определенного комплекса условий S, в которых наблюдается то или иное явление и фиксируется некоторый результат, как характеристика явления.

События, как правило, обозначают заглавными буквами латинского алфавита: A, B, C и т.д.

Каждое событие A обладает определенной степенью объективной возможности наступления в результате проведения испытания. Численную меру такой возможности обозначают P(A).

Вероятностью P(A) случайного события A называется объективная численная мера, от 0 до 1, возможности наблюдать случайное событие A в результате проведения испытания при определенных условиях S.

Несколько событий образуют полную группу попарно несовместных событий, если в результате испытания наступает одно и только одно из этих событий.

События называются равновозможными, если в результате испытания ни одно из них не является объективно более возможным, чем другие.

События называются несовместными, если наступление одного (любого) из них исключает наступление других событий в одном и том же испытании.

События называются совместными, если наступление одного (любого) из них не исключает появления других событий в одном и том же испытании.

Пусть исходы некоторого испытания образуют полную группу равновозможных случайных событий. Такие исходы называются элементарными исходами, случаями или шансами. Те элементарные исходы, в которых наступает случайное событие A, называются благоприятствующими (или благоприятными) этому событию.

На подсчете числа исходов испытания, благоприятствующих данному событию A, и его отношения к общему числу равновозможных исходов, основано так называемое классическое определение вероятности события A.

Классическим определением вероятности P(A)случайного события A называют отношение числа m, благоприятствующих этому событию исходов испытания, к общему числу n всех равновозможных несовместных элементарных исходов, образующих полную группу попарно несовместных событий:

(1)

Так как для любого события 0  m  n, то согласно (1) вероятность случайного события A есть неотрицательное число, заключенное между 0 и 1:

0  P(A)  1.

Событие A, которое в результате испытания обязательно должно произойти, называется достоверным. Для достоверного события всегда m = n и, следовательно,

P(A) = 1.

Событие A, которое в результате испытания не может произойти, называется невозможным. Для невозможного события всегда m = 0 и, следовательно,

P(A) = 0.

Мы ввели три понятия  «опыт», «случайное событие», «вероятность случайного события», которые являются фундаментальными понятиями теории вероятностей и могут быть интерпретированы с помощью абстрактной урновой модели (урны). Урну представим как некоторый недоступный для рассмотрения содержимого ящик, в котором находятся однородные предметы. Опыт заключается в том, что предметы тщательно размешивают и наудачу извлекается один предмет. Лотерейный барабан с размещенными в нем лотерейными билетами или шариками можно использовать в качестве физического аналога абстрактной урновой модели. Например, пусть в урне размещены n одинаковых по весу и размерам, но разных по цвету шаров: m₁ — белых, m₂ — синих, m₃ — красных.

Все шары тщательно размешивают и наудачу извлекается один шар. Результат одного планируемого опыта в силу заранее неизвестных причин заранее неизвестен. Однако он может быть охарактеризован с помощью понятий «случайное событие» и «вероятность случайного события» следующим образом. Очевидно, что появление каждого шара есть случайное событие, которое может либо произойти, либо не произойти. Назовем это событие элементарным и обозначим через E_i, Возможность в качестве результата опыта наблюдать каждый шар, очевидно, одна и та же.

Численно определим эту возможность отношением т.е. В результате одного планируемого опыта мы будем наблюдать либо событие A — появление шара белого цвета, либо событие В — появление шара синего цвета, либо событие С — появление шара красного цвета. Эти события образуют полную группу несовместных событий, каждое из которых имеет разную возможность быть наблюдаемым в силу Как численно определить возможность наблюдать события A, В и С?Очевидно также, что поскольку она определяется числом шаров соответствующего цвета, то согласно классическому определению вероятности случайного события

(2)

Обратим внимание на существенное обстоятельство наших рассуждений: никаких опытов мы не проводили, но с помощью урновой модели умозрительно ввели понятия «опыта», «случайного события» и «вероятности случайного события». Предположим теперь, что опыт проведен Nраз и получены результаты: — числа наблюдений соответственно белого, синего и красного шаров, M₁ + M₂ + M₃ = N. Возьмем отношение

(3)

Величина W(·) (3) называется относительной частотой наблюдения случайного события (·).

Очевидно, что

(4)

где P(·) — вероятность случайного события (·).

Французский учений Бюффон подбрасывая монету N раз доказал, что относительная частота выпадения герба W(G) может служить оценкой вероятности выпадения герба P(G):

(5)

причем тем точнее, чем больше N. Так был установлен закон устойчивости относительной частоты случайного события: чем больше число N опытов, тем относительная частота случайного события W(·) ближе к вероятности случайного события P(·), т.е.

(6)

Закон (6) позволяет утверждать о том, что вероятность случайного события P(·), как численная мера возможности его наблюдения, является объективным понятием.

Для решения задач с использованием классического определения вероятности необходимо знать основные правила и формулы комбинаторики — раздела математики, использующего методы решения комбинаторных задач на подсчет числа различных комбинаций. В частности, если комбинации из n элементов по k отличаются хотя бы одним элементом, то их называют сочетаниями из n элементов по k. Число таких сочетаний равно

(7)

где (8)

По определению 0! = 1.

Имеет место следующее свойство сочетаний:


Пример 1. На складе находятся 30 телевизоров, 5 из которых имеют скрытые дефекты. Случайным образом выбраны 3 телевизора. Найти вероятность того, что ни один из выбранных телевизоров не будет иметь дефектов.

Решение. Общее число возможных элементарных исходов испытания (выбора 3х телевизоров) равно числу способов, которыми можно выбрать 3 телевизора из 30, находящихся на складе, т.е. числу сочетаний из 30 по 3:



Подсчитаем число исходов, благоприятствующих интересующему нас событию: среди выбранных трех телевизоров не будет ни одного, имеющего дефекты. Число таких исходов равно числу способов, которыми можно выбрать 3 телевизора из находящихся на складе 25 телевизоров, не имеющих дефекты, т.е. числу сочетаний из 25 по 3:



Искомая вероятность равна отношению числа исходов, благоприятствующих рассматриваемому событию, к общему числу возможных элементарных исходов:



Теперь вычислим значения 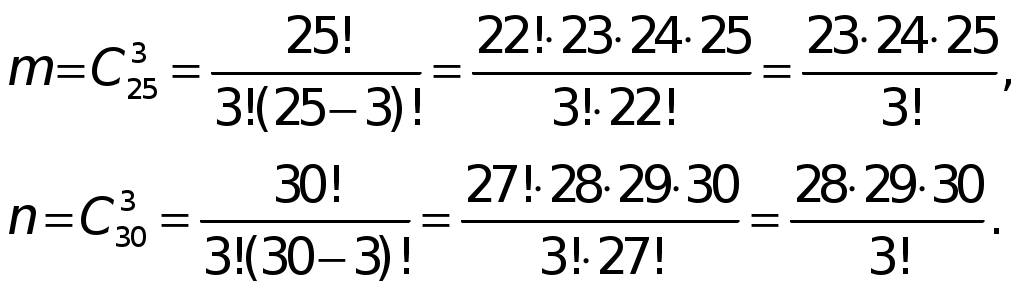и Согласно формулам (7) и (8) соответственно находим:



Следовательно, искомая вероятность равна



Ответ: Вероятность того, что 3 случайным образом выбранные телевизора не будут иметь дефекты, равна 0,567.

2. Алгебра событий

В теории вероятностей очень важными понятиями являются понятия суммы и произведения событий.

Суммой двух событий A₁ и A₂ называется событие, состоящее в появлении события A₁, или A₂, или обоих событий.

Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий:



Произведением (или совмещением) нескольких событий называется событие, состоящее в одновременном появлении всех этих событий:



Событие состоящее в ненаступлении события А, называется противоположным к событию А. При этом — достоверное событие, — невозможное событие.

3. Теорема сложения вероятностей несовместных событий

Пусть случайные события А и В — несовместны, причем известны вероятности этих событий.

Теорема 1. Вероятность суммы А + В двух несовместных событий А и В равна сумме вероятностей этих событий:

Р(А + В) = Р(А) + Р(В). (9)

Следствие 1. Вероятность наступления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

(10)

Следствие 2. Сумма вероятностей событий A₁,A₂,…,A_n, образующих полную группу попарно несовместных событий, равна единице:

Р(A₁) + Р(A₂) +……+ Р(A_n) = 1. (11)

Следствие 3. Сумма вероятностей противоположных событий равна единице:

Р(А) + Р = 1. (12)

4. Теорема умножения вероятностей

В основе определения вероятности случайного события Р(А) лежит некоторый фиксированный комплекс условий S проведения испытания. Если никаких ограничений, кроме условий S, при вычислении вероятности Р(А) не налагается, то такая вероятность называется безусловной. Однако часто требуется вычислить вероятность события А при дополнительном условии, что произошло некоторое событие В.

Вероятность наступления события А, вычисленная при условии наступления события В, называется условной вероятностью события А по отношению к событию В и обозначается илиP_B(А).

Теорема 2. Вероятность произведения двух событий равна произведению вероятности одного (любого) из этих событий на условную вероятность другого события относительно первого:

Р(АВ) = Р(А) Р( ) = Р(В) Р( ). (13)

Теорема умножения вероятностей обобщается на случай произвольного числа событий:

(14)

т.е. вероятность произведения нескольких событий равна произведению условных вероятностей каждого из этих событий. При этом условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли.

Согласно (13) значения условных вероятностей равны:



Событие А называется независимым от события В, если наступление события В не изменяет вероятности наступления события А, т.е. условная вероятность события А относительно события В равна его безусловной вероятности:

Р(А/В) = Р(А).

Для независимых событий теорема умножения вероятностей принимает вид:

Р(АВ) = Р(А) Р(В), (15)

т.е. вероятность совместного наступления двух независимых событий равна произведению вероятностей этих событий.

Для п независимых событий А₁, A₂,…,A_nтеорема умножения вероятностей принимает вид:

= Р(А₁) Р(А₂) ... Р(А_п). (16)