Вариант 25. Контрольное задание по теме 3 Линейное программирование. 3

• Название: Контрольное задание по теме 3 Линейное программирование. 3
• Дата: 16.11.2018
• Размер: 1.21 Mb.
• Имя файла: Вариант 25.doc
• Тип: Документы; #56634
• страница: 3 из 13

Контрольное задание по теме 4.4.

«Математические основы сетевого моделирования».

1. 
   Построить фрагмент сетевого графика согласно заданного порядка предшествования.
   

A, B << C

C, D << E

A, D << G

C, G << H
2. Расчет временных параметров сетевой модели и приведение критического времени к заданному сроку.

2.1. Рассчитать временные параметры:

T ⁰_i – ранние сроки свершения событий;

T¹_i – поздние сроки свершения событий;

Ткр – критическое время и определить критический путь (КП);

Rⁿ_ij – полные резервы работ;

R^с_ij – свободные резервы работ;

2.2. Привести Ткр к Тдир.

3. 
   Выполнить перерасчет временных параметров.
   
4. 
   Вычертить календарный график работ в масштабе времени в ранние сроки (линейную диаграмму).
   

Рисунок 2. 25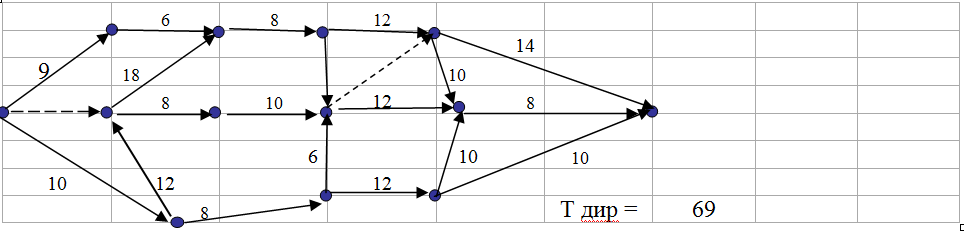


Решение
1. Построим фрагмент сетевого графика согласно заданного порядка предшествования.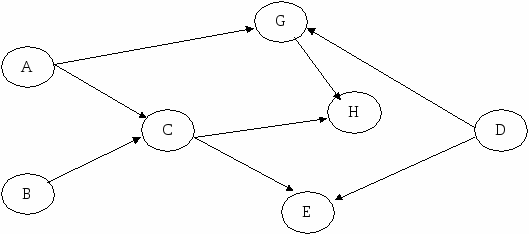

2. Произведем расчет временных параметров сетевой модели и приведение критического времени к заданному сроку.

Резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ.

Для определения резервов времени по событиям сети рассчитывают наиболее ранние t^p и наиболее поздние t^п сроки свершения событий. Любое событие не может наступить прежде, чем свершаться все предшествующие ему события и не будут выполнены все предшествующие работы. Поэтому ранний (или ожидаемый) срок tp(i) свершения i-ого события определяется продолжительностью максимального пути, предшествующего этому событию:

t^p(i) = max(t(L_ni))

где L_ni – любой путь, предшествующий i-ому событию, то есть путь от исходного до i-ого события сети.

Если событие j имеет несколько предшествующих путей, а следовательно, несколько предшествующих событий i, то ранний срок свершения события j удобно находить по формуле:

t^p(j) = max[t^p(i) + t(i,j)]

Задержка свершения события i по отношению к своему раннему сроку не отразится на сроке свершения завершающего события (а значит, и на сроке выполнения комплекса работ) до тех пор, пока сумма срока свершения этого события и продолжительности (длины) максимального из следующих за ним путей не превысит длины критического пути. Поэтому поздний (или предельный) срок t^п(i) свершения i-ого события равен:

t^п(i) = t_kp - max(t(L_ci))

где L_ci - любой путь, следующий за i-ым событием, т.е. путь от i-ого до завершающего события сети.

Если событие i имеет несколько последующих путей, а следовательно, несколько последующих событий j, то поздний срок свершения события i удобно находить по формуле:

t^п(i) = min[t^п(j) - t(i,j)]

Резерв времени R(i) i-ого события определяется как разность между поздним и ранним сроками его свершения:

R(i) = t^п(i) - t^p(i)

Резерв времени события показывает, на какой допустимый период времени можно задержать наступление этого события, не вызывая при этом увеличения срока выполнения комплекса работ.

Критические события резервов времени не имеют, так как любая задержка в свершении события, лежащего на критическом пути, вызовет такую же задержку в свершении завершающего события. Таким образом, определив ранний срок наступления завершающего события сети, мы тем самым определяем длину критического пути.

При определении ранних сроков свершения событий tp(i) двигаемся по сетевому графику слева направо и используем формулы (1), (2).

Произведем расчет сроков свершения событий.

Для i=1 (начального события), очевидно tp(1)=0.

i=2: t^p(2) = t^p(1) + t(1,2) = 0 + 9 = 9.

i=3: t^p(3) = t^p(1) + t(1,3) = 0 + 10 = 10.

i=4: t^p(4) = t^p(2) + t(2,4) = 9 + 6 = 15.

i=5: t^p(5) = t^p(3) + t(3,5) = 10 + 12 = 22.

i=6: t^p(6) = t^p(5) + t(5,6) = 22 + 8 = 30.

i=7: t^p(7) = t^p(6) + t(6,7) = 30 + 10 = 40.

i=8: t^p(8) = t^p(3) + t(3,8) = 10 + 8 = 18.

i=9: t^p(9) = t^p(4) + t(4,9) = 15 + 8 = 23.

i=10: t^p(10) = t^p(9) + t(9,10) = 23 + 12 = 35.

i=11: max(t^p(7) + t(7,11);t^p(10) + t(10,11)) = max(40 + 12;35 + 10) = 52.

i=12: t^p(12) = t^p(8) + t(8,12) = 18 + 12 = 30.

i=13: max(t^p(10) + t(10,13);t^p(11) + t(11,13);t^p(12) + t(12,13)) =

= max(35 + 14;52 + 8;30 + 10) = 60.

Длина критического пути равна раннему сроку свершения завершающего события 13: t_kp=tp(13)=60

При определении поздних сроков свершения событий t_п(i) двигаемся по сети в обратном направлении, то есть справа налево и используем формулы (3), (4).

Для i=13 (завершающего события) поздний срок свершения события должен равняться его раннему сроку (иначе изменится длина критического пути): t^п(13)= t^р(13)=60.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 11. Просматриваются все строчки, начинающиеся с номера 11.

i=11: t^п(11) = t^п(13) - t(11,13) = 60 - 8 = 52.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 11. Просматриваются все строчки, начинающиеся с номера 11.

i=11: t^п(11) = t^п(13) - t(11,13) = 60 - 8 = 52.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 10. Просматриваются все строчки, начинающиеся с номера 10.

i=10: min(t^п(11) - t(10,11);t^п(13) - t(10,13)) = min(52 - 10;60 - 14) = 42.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 12. Просматриваются все строчки, начинающиеся с номера 12.

i=12: min(t^п(11) - t(12,11);t^п(13) - t(12,13)) = min(52 - 10;60 - 10) = 42.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 11. Просматриваются все строчки, начинающиеся с номера 11.

i=11: t^п(11) = t^п(13) - t(11,13) = 60 - 8 = 52.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 7. Просматриваются все строчки, начинающиеся с номера 7.

i=7: t^п(7) = t^п(11) - t(7,11) = 52 - 12 = 40.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 6. Просматриваются все строчки, начинающиеся с номера 6.

i=6: t^п(6) = t^п(7) - t(6,7) = 40 - 10 = 30.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 4. Просматриваются все строчки, начинающиеся с номера 4.

(4,9): 0 - 8 = -8;

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 9. Просматриваются все строчки, начинающиеся с номера 9.

i=9: t^п(9) = t^п(10) - t(9,10) = 42 - 12 = 30.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 8. Просматриваются все строчки, начинающиеся с номера 8.

i=8: t^п(8) = t^п(12) - t(8,12) = 42 - 12 = 30.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 5. Просматриваются все строчки, начинающиеся с номера 5.

(5,4): 0 - 18 = -18;

i=5: min(t^п(6) - t(5,6);t^п() - t) = min(30 - 8; - ) = 0.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 4. Просматриваются все строчки, начинающиеся с номера 4.

i=4: t^п(4) = t^п(9) - t(4,9) = 30 - 8 = 22.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 3. Просматриваются все строчки, начинающиеся с номера 3.

(3,5): 0 - 12 = -12;

i=3: min(t^п(8) - t(3,8);t^п() - t) = min(30 - 8; - ) = 0.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 2. Просматриваются все строчки, начинающиеся с номера 2.

i=2: t^п(2) = t^п(4) - t(2,4) = 22 - 6 = 16.

Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 1. Просматриваются все строчки, начинающиеся с номера 1.

(1,3): 0 - 10 = -10;

i=1: min(t^п(2) - t(1,2);t^п() - t) = min(16 - 9; - ) = 0.

Таблица 1

Расчет резерва работ

Номер события	Сроки свершения события: ранний tp(i)	Сроки свершения события: поздний tп(i)	Резерв времени, R(i)
1	0	0	0
2	9	16	7
3	10	0	-10
4	15	22	7
5	22	0	-22
6	30	30	0
7	40	40	0
8	18	30	12
9	23	30	7
10	35	42	7
11	52	52	0
12	30	42	12
13	60	60	0

Заполнение таблицы 2.

Перечень работ и их продолжительность перенесем во вторую и третью графы. При этом работы следует записывать в графу 2 последовательно: сначала начиная с номера 1, затем с номера 2 и т.д.

Во второй графе поставим число, характеризующее количество непосредственно предшествующих работ (КПР) тому событию, с которого начинается рассматриваемая работа.

Так, для работы (11,13) в графу 1 поставим число 2, т.к. на номер 11 оканчиваются 2 работы: (7,11),(10,11),(12,11).

Графу 4 получаем из таблицы 1 (t^p(i)). Графу 7 получаем из таблицы 1 (t^п(i)).

Значения в графе 5 получаются в результате суммирования граф 3 и 4.

В графе 6 позднее начало работы определяется как разность позднего окончания этих работ и их продолжительности (из значений графы 7 вычитаются данные графы 3);

Содержимое графы 8 (полный резерв времени R(ij)) равно разности граф 6 и 4 или граф 7 и 5. Если R(ij) равен нулю, то работа является критической

Таблица 2

Анализ сетевой модели по времени

Работа (i,j)	Количество предшествующих работ	Продолжительность tij	Ранние сроки: начало tijР.Н.	Ранние сроки: окончание tijР.О.	Поздние сроки: начало tijП.Н.	Поздние сроки: окончание tijП.О.	Резервы времени: полный RijП	Независимый резерв времени RijН	Частный резерв I рода, Rij1	Частный резерв II рода, RijC
(1,2)	0	9	0	9	7	16	7	0	7	0
(1,3)	0	10	0	10	-10	0	-10	0	-10	0
(2,4)	1	6	9	15	16	22	7	-7	0	0
(3,5)	1	12	10	22	-12	0	-22	10	-12	0
(3,8)	1	8	10	18	22	30	12	10	22	0
(4,9)	1	8	15	23	22	30	7	-7	0	0
(5,4)	1	18	22	40	-18	0	-40	-25	-18	-47
(5,6)	1	8	22	30	22	30	0	22	22	0
(6,7)	1	10	30	40	30	40	0	0	0	0
(7,11)	1	12	40	52	40	52	0	0	0	0
(8,12)	1	12	18	30	30	42	12	-12	0	0
(9,10)	1	12	23	35	30	42	7	-7	0	0
(10,11)	1	10	35	45	42	52	7	0	0	7
(10,13)	1	14	35	49	46	60	11	4	4	11
(11,13)	2	8	52	60	52	60	0	0	0	0
(12,11)	1	10	30	40	42	52	12	0	0	12
(12,13)	1	10	30	40	50	60	20	8	8	20

Следует отметить, что кроме полного резерва времени работы, выделяют еще три разновидности резервов. Частный резерв времени первого вида R₁ - часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока ее начального события. R₁ находится по формуле:

R(i,j)= R^п(i,j) - R(i)

Частный резерв времени второго вида, или свободный резерв времени Rc работы (i,j) представляет собой часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события. Rc находится по формуле:

R(i,j)= R^п(i,j) - R(j)

Значение свободного резерва времени работы указывает на расположение резервов, необходимых для оптимизации.

Независимый резерв времени Rн работы (i,j) - часть полного резерва, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие начинаются в ранние сроки. Rн находится по формуле:

R(i,j)= R^п(i,j)- R(i) - R(j)

Критический путь: (1,3)(3,5)(5,6)(6,7)(7,11)(11,13).

Продолжительность критического пути: 82.

Проведем анализ сетевого графика.

Сложность сетевого графика оценивается коэффициентом сложности, который определяется по формуле:

K_c = n_pab / n_cob

где K_c – коэффициент сложности сетевого графика; n_pab – количество работ, ед.; n_cob – количество событий, ед.

Сетевые графики, имеющие коэффициент сложности от 1,0 до 1,5, являются простыми, от 1,51 до 2,0 – средней сложности, более 2,1 – сложными.

K_c = 18 / 13 = 1.38

Поскольку Kc < 1.5, то сетевой график является простым.

Построим диаграмму Ганта и карту проекта:
Диаграмма Ганта