Вариант 25. Контрольное задание по теме 3 Линейное программирование. 3
 Скачать 1.21 Mb. Скачать 1.21 Mb.
|
|
Содержание Контрольное задание по теме 4.2. 3 «Линейное программирование». 3 Контрольное задание по теме 4.3. 21 «Задачи транспортного типа». 21 Контрольное задание по теме 4.4. 34 «Математические основы сетевого моделирования». 34 Карта проекта 43 Контрольное задание по теме 4.6. 46 «Задачи управления запасами». 46 Статическая модель 47 Контрольное задание по теме 4.7. 48 «Теория массового обслуживания». 48 Контрольное задание по теме 4.8. 54 «Состязательные задачи». 54 Контрольное задание по теме 4.9. 58 «Динамическое программирование». 58 Контрольное задание по теме 4.10. 59 «Имитационное моделирование». 59 Контрольное задание по теме 4.11 61 «Многокритериальная оптимизация» 61 Список использованной литературы 80 Контрольное задание по теме 4.2.«Линейное программирование».Составить математическую модель задачи линейного программирования и найти решение геометрическим способом.
Таблица 1
Решение Составим целевую функцию задачи линейного программирования с ограничивающими условиями. Введем обозначения: х1 – изделие 1; х2 – изделие 2. Учитывая, что ресурсы не могут быть отрицательным, должны выполняться следующие неравенства для полученной целевой функции: 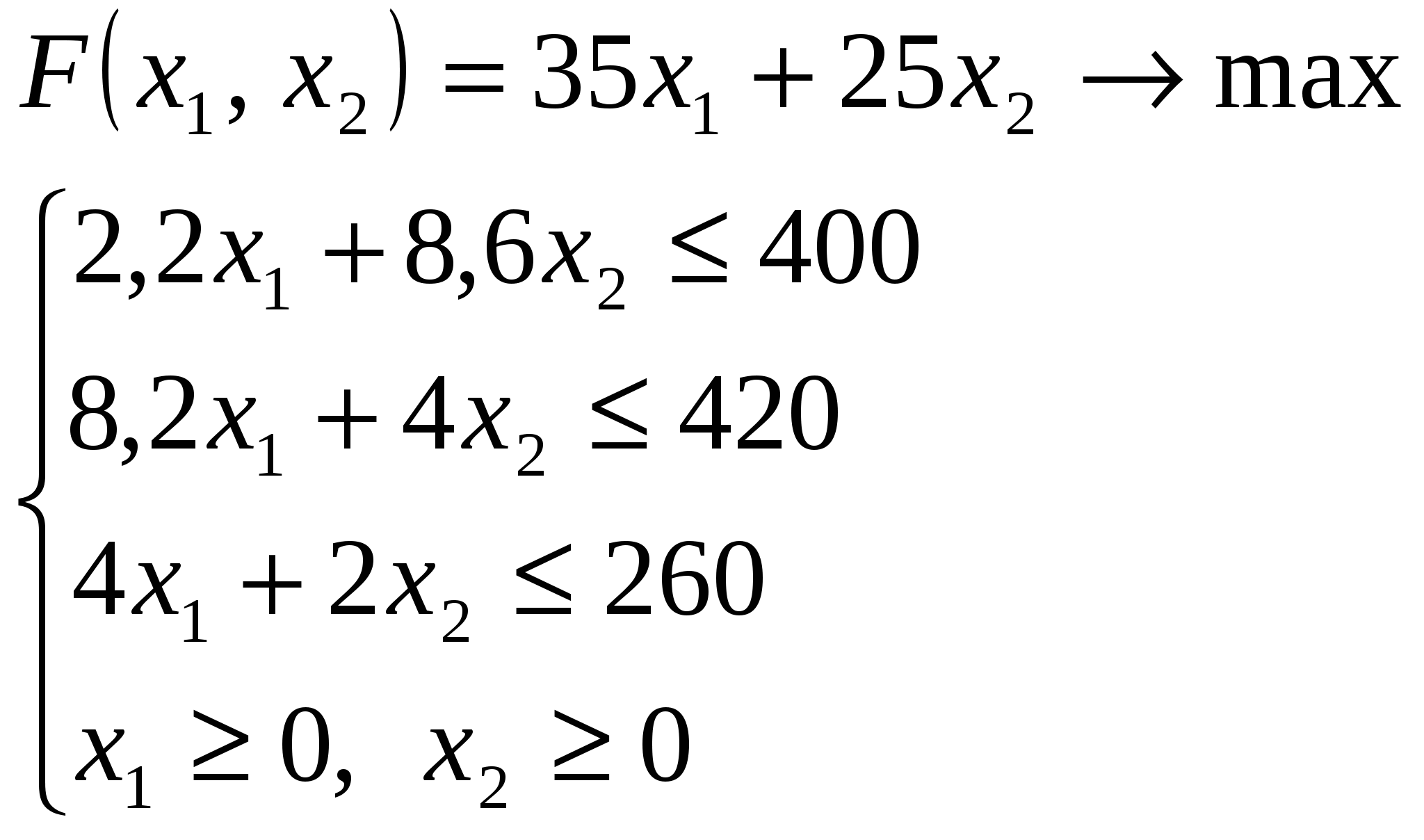 1. Решим данную задачу графическим способом. Построим область допустимых решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом). Построим уравнение 2.2x1+8.6x2 = 400 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 46.51. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 181.82. Соединяем точку (0;46.51) с (181.82;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 2.2 • 0 + 8.6 • 0 - 400 ≤ 0, т.е. 2.2x1+8.6x2 - 400≤ 0 в полуплоскости ниже прямой. Построим уравнение 8.2x1+4x2 = 420 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 105. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 51.22. Соединяем точку (0;105) с (51.22;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 8.2 • 0 + 4 • 0 - 420 ≤ 0, т.е. 8.2x1+4x2 - 420≤ 0 в полуплоскости ниже прямой. Построим уравнение 4x1+2x2 = 260 по двум точкам. Для нахождения первой точки приравниваем x1 = 0. Находим x2 = 130. Для нахождения второй точки приравниваем x2 = 0. Находим x1 = 65. Соединяем точку (0;130) с (65;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 4 • 0 + 2 • 0 - 260 ≤ 0, т.е. 4x1+2x2 - 260≤ 0 в полуплоскости ниже прямой. 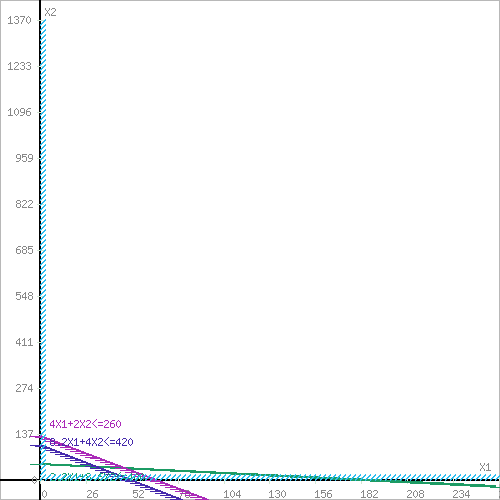 или 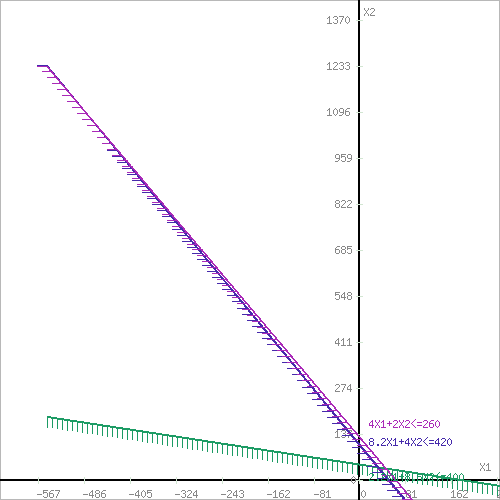 Границы области допустимых решений Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи. Обозначим границы области многоугольника решений. 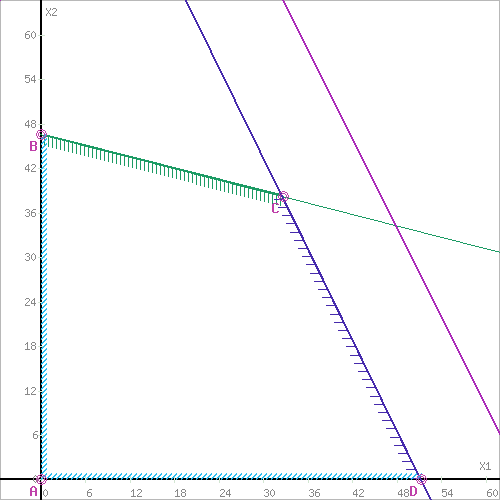 Рассмотрим целевую функцию задачи F = 35x1+25x2 → max. Построим прямую, отвечающую значению функции F = 0: F = 35x1+25x2 = 0. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). Начало вектора – точка (0; 0), конец – точка (35; 25). Будем двигать эту прямую параллельным образом. Поскольку нас интересует максимальное решение, поэтому двигаем прямую до последнего касания обозначенной области. На графике эта прямая обозначена пунктирной линией. 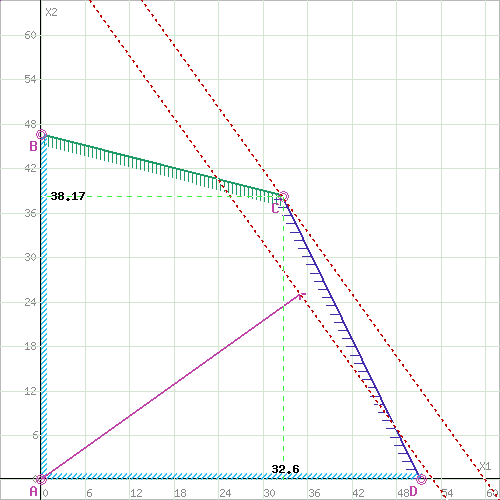 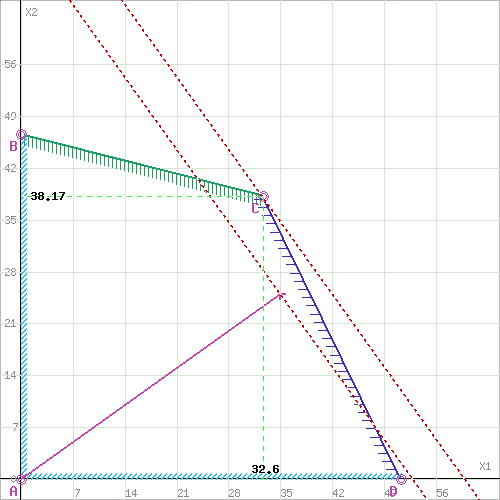 Область допустимых решений представляет собой треугольник. Прямая F(x) = const пересекает область в точке C. Так как точка C получена в результате пересечения прямых (1) и (2), то ее координаты удовлетворяют уравнениям этих прямых: 2.2x1+8.6x2=400 8.2x1+4x2=420 Решив систему уравнений, получим: x1 = 32.5988, x2 = 38.1724. Откуда найдем максимальное значение целевой функции: F(X) = 35*32.5988 + 25*38.1724 = 2095.269 2. Решим задачу симплексным методом. Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы Определим максимальное значение целевой функции F(X) = 35x1+25x2 при следующих условиях-ограничениях: 2.2x1+8.6x2≤400 8.2x1+4x2≤420 4x1+2x2≤260 Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме). В 1-м неравенстве смысла (≤) вводим базисную переменную x3. В 2-м неравенстве смысла (≤) вводим базисную переменную x4. В 3-м неравенстве смысла (≤) вводим базисную переменную x5. 2.2x1 + 8.6x2 + 1x3 + 0x4 + 0x5 = 400 8.2x1 + 4x2 + 0x3 + 1x4 + 0x5 = 420 4x1 + 2x2 + 0x3 + 0x4 + 1x5 = 260 Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид: Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом. Экономический смысл дополнительных переменных: дополнительные переменные задачи ЛП обозначают излишки сырья, времени, других ресурсов, остающихся в производстве данного оптимального плана. Решим систему уравнений относительно базисных переменных: x3, x4, x5 Полагая, что свободные переменные равны 0, получим первый опорный план: X1 = (0,0,400,420,260) Базисное решение называется допустимым, если оно неотрицательно.
Переходим к основному алгоритму симплекс-метода. Итерация №0. 1. Проверка критерия оптимальности. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. 2. Определение новой базисной переменной. В индексной строке F(x) выбираем максимальный по модулю элемент. В качестве ведущего выберем столбец, соответствующий переменной x1, так как это наибольший коэффициент по модулю. 3. Определение новой свободной переменной. Вычислим значения Di по строкам как частное от деления: bi / ai1 и из них выберем наименьшее: Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (8.2) и находится на пересечении ведущего столбца и ведущей строки.
4. Пересчет симплекс-таблицы. Формируем следующую часть симплексной таблицы. Вместо переменной x4 в план 1 войдет переменная x1. Строка, соответствующая переменной x1 в плане 1, получена в результате деления всех элементов строки x4 плана 0 на разрешающий элемент РЭ=8.2 На месте разрешающего элемента в плане 1 получаем 1. В остальных клетках столбца x1 плана 1 записываем нули. Таким образом, в новом плане 1 заполнены строка x1 и столбец x1 . Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ. НЭ = СЭ - (А*В)/РЭ СТЭ - элемент старого плана, РЭ - разрешающий элемент (8.2), А и В - элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ. Представим расчет каждого элемента в виде таблицы:
После преобразований получаем новую таблицу:
Итерация №1. 1. Проверка критерия оптимальности. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. 2. Определение новой базисной переменной. В индексной строке F(x) выбираем максимальный по модулю элемент. В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю. 3. Определение новой свободной переменной. Вычислим значения Di по строкам как частное от деления: bi / ai2 и из них выберем наименьшее: Следовательно, 1-ая строка является ведущей. Разрешающий элемент равен (7.53) и находится на пересечении ведущего столбца и ведущей строки.
4. Пересчет симплекс-таблицы. Формируем следующую часть симплексной таблицы. Вместо переменной x3 в план 2 войдет переменная x2 Строка, соответствующая переменной x2 в плане 2, получена в результате деления всех элементов строки x3 плана 1 на разрешающий элемент РЭ=7.53 На месте разрешающего элемента в плане 2 получаем 1. В остальных клетках столбца x2 плана 2 записываем нули. Таким образом, в новом плане 2 заполнены строка x2 и столбец x2 . Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
После преобразований получаем новую таблицу:
1. Проверка критерия оптимальности. Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы:
Оптимальный план можно записать так: x2 = 38.17 x1 = 32.6 F(X) = 25 • 38.17 + 35 • 32.6 = 2095.2689565791 Построим двойственную задачу по следующим правилам. 1. Количество переменных в двойственной задаче равно количеству неравенств в исходной. 2. Матрица коэффициентов двойственной задачи является транспонированной к матрице коэффициентов исходной. 3. Система ограничений двойственной задачи записывается в виде неравенств противоположного смысла неравенствам системы ограничений прямой задачи. Столбец свободных членов исходной задачи является строкой коэффициентов для целевой функции двойственной. Целевая функция в одной задаче максимизируется, в другой минимизируется. Расширенная матрица A:
Транспонированная матрица AT:
Условиям неотрицательности переменных исходной задачи соответствуют неравенства-ограничения двойственной, направленные в другую сторону. И наоборот, неравенствам-ограничениям в исходной соответствуют условия неотрицательности в двойственной. Неравенства, соединенные стрелочками (↔), называются сопряженными. Решение двойственной задачи дает оптимальную систему оценок ресурсов. Выясним экономический смысл двойственной задачи. Заметим, что каждое слагаемое в левой части ограничений должно измеряться в тех же единицах, что и правая. Целевая функция в двойственной задаче определяет стоимость запасов всех ресурсов. Левая часть ограничений определяет стоимость ресурсов в теневых (альтернативных) ценах, затраченных на xj. 2.2y1+8.2y2+4y3≥35 8.6y1+4y2+2y3≥25 400y1+420y2+260y3 → min y1 ≥ 0 ,y2 ≥ 0 , y3 ≥ 0
Переменные yj называются допустимым решением двойственной задачи. Переменные yj называются оптимальными, если они допустимые и на них целевая функция достигает минимальное значения. Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи. Из первой теоремы двойственности следует, что Y = C*A-1. Составим матрицу A из компонентов векторов, входящих в оптимальный базис: Определив обратную матрицу D = А-1 через алгебраические дополнения, получим: Как видно из последнего плана симплексной таблицы, обратная матрица A-1 расположена в столбцах дополнительных переменных . Тогда Y = C*A-1 = Оптимальный план двойственной задачи равен: y1 = 1.05 y2 = 3.99 y3 = 0 Z(Y) = 400*1.05+420*3.99+260*0 = 2095.27 Критерий оптимальности полученного решения. Если существуют такие допустимые решения X и Y прямой и двойственной задач, для которых выполняется равенство целевых функций F(x) = Z(y), то эти решения X и Y являются оптимальными решениями прямой и двойственной задач соответственно. Определение дефицитных и недефицитных (избыточных) ресурсов. Вторая теорема двойственности. Подставим оптимальный план прямой задачи в систему ограниченной математической модели: 2.2*32.6 + 8.6*38.17 = 400 = 400 8.2*32.6 + 4*38.17 = 420 = 420 4*32.6 + 2*38.17 = 206.74 < 260 1-ое ограничение прямой задачи выполняется как равенство. Это означает, что 1-ый ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y1>0). 2-ое ограничение прямой задачи выполняется как равенство. Это означает, что 2-ый ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y2>0). 3-ое ограничение выполняется как строгое неравенство, т.е. ресурс 3-го вида израсходован не полностью. Значит, этот ресурс не является дефицитным и его оценка в оптимальном плане y3 = 0. Неиспользованный экономический резерв ресурса 3 составляет 53.26 (260-206.74). Этот резерв не может быть использован в оптимальном плане, но указывает на возможность изменений в объекте моделирования (например, резерв ресурса можно продать или сдать в аренду). Таким образом, отличную от нуля двойственные оценки имеют лишь те виды ресурсов, которые полностью используются в оптимальном плане. Поэтому двойственные оценки определяют дефицитность ресурсов. Обоснование эффективности оптимального плана. При подстановке оптимальных двойственных оценок в систему ограничений двойственной задачи получим: 2.2*1.05 + 8.2*3.99 + 4*0 = 35 = 35 8.6*1.05 + 4*3.99 + 2*0 = 25 = 25 1-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 1-ый ресурс экономически выгодно использовать, а его использование предусмотрено оптимальным планом прямой задачи (x1>0). 2-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 2-ый ресурс экономически выгодно использовать, а его использование предусмотрено оптимальным планом прямой задачи (x2>0). Анализ устойчивости оптимального плана. Проведем анализ устойчивости оптимального плана и оценим степень влияния изменения ресурсов на значение целевой функции. Чувствительность решения к изменению коэффициентов целевой функции. Так как любые изменения коэффициентов целевой функции оказывают влияние на оптимальность полученного ранее решения, то наша цель - найти такие диапазоны изменения коэффициентов в целевой функции (рассматривая каждый из коэффициентов отдельно), при которых оптимальные значения переменных остаются неизменными. Пусть каждое значение параметра целевой функции изменится на ∆ сi. Найдем интервалы, при которых будет экономически выгодно использование ресурсов. Допустимые диапазоны изменения коэффициентов в целевой функции определятся из соотношений: 2-ый параметр целевой функции может изменяться в пределах: ∆c2- = min [yk/d2k] для d2k>0. ∆c2+ = |max [yk/d2k]| для d2k<0. где в знаменателе коэффициенты столбцов свободных переменных в оптимальном плане (коэффициенты структурных сдвигов, элементы обратной матрицы к базису оптимального плана). Таким образом, 2-параметр может быть уменьшен на 7.93 или увеличен на 111.82 Интервал изменения равен: (c2 - ∆c2-; c2 + ∆c2+) [25-7.93; 25+111.82] = [17.07;136.82] Если значение c2 будет лежать в данном интервале, то оптимальный план не изменится. 1-ый параметр целевой функции может изменяться в пределах: ∆c1- = min [yk/d1k] для d1k>0. ∆c1+ = |max [yk/d1k]| для d1k<0. Таким образом, 1-параметр может быть уменьшен на 28.6 или увеличен на 16.25 Интервал изменения равен: (c1 - ∆c1-; c1 + ∆c1+) [35-28.6; 35+16.25] = [6.4;51.25] Если значение c1 будет лежать в данном интервале, то оптимальный план не изменится. Чувствительность решения к изменению запасов сырья. Из теоремы об оценках известно, что колебание величины bi приводит к увеличению или уменьшению f(X). Оно определяется величиной yi в случае, когда при изменении величин bi значения переменных уi в оптимальном плане соответствующей двойственной задачи остаются неизменными. Поэтому необходимо найти такие интервалы изменения каждого из свободных членов системы ограничений исходной ЗЛП, в которых оптимальный план двойственной задачи не менялся бы. Найдем интервалы устойчивости ресурсов. 1-ый запас может изменяться в пределах: ∆b1- = min [xk/dk1] для dk1>0. ∆b1+ = |max [xk/dk1]| для dk1<0. Таким образом, 1-ый запас может быть уменьшен на 287.32 или увеличен на 503 Интервал изменения равен: (b1 - ∆b1-; b1 + ∆b1+) [400-287.32; 400+503] = [112.68;903] 2-ый запас может изменяться в пределах: ∆b2- = min [xk/dk2] для dk2>0. ∆b2+ = |max [xk/dk2]| для dk2<0. Таким образом, 2-ый запас может быть уменьшен на 233.95 или увеличен на 109.57 Интервал изменения равен: (b2 - ∆b2-; b2 + ∆b2+) [420-233.95; 420+109.57] = [186.05;529.57] Нижняя граница для: ∆b-3 ∆b-3 = min[xk/dk3] для dk3>0. Таким образом, 3-ый запас может быть уменьшен на 53.26. 3-ый вид ресурса в оптимальном плане недоиспользован, является недефицитным. Увеличение данного ресурса приведет лишь к росту его остатка. При этом структурных изменений в оптимальном плане не будет, так как двойственная оценка y3 = 0. Другими словами, верхняя граница b+3 = +∞ Интервал изменения равен: (b3 - ∆b3-; ∞) [260-53.26; +∞] = [206.74;+∞] | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
