Вариант 25. Контрольное задание по теме 3 Линейное программирование. 3
 Скачать 1.21 Mb.
|
Контрольное задание по теме 4.7.«Теория массового обслуживания».1   . Построить модель многоканальной системы массового обслуживания с бесконечной очередью. Вычислить nw – среднее число клиентов, ожидающих обслуживания, tw – среднее время ожидания обслуживания, W – вероятность обязательного пребывания в очереди и Р0 – вероятность простаивания всех каналов обслуживания. 2. Построить модель многоканальной системы массового обслуживания с ограниченной очередью. Вычислить nw – среднее число клиентов, ожидающих обслуживания, tw – среднее время ожидания обслуживания, W – вероятность обязательного пребывания в очереди и Р0 – вероятность простаивания всех каналов обслуживания.
Решение 1. Построим модель многоканальной системы массового обслуживания с бесконечной очередью. Исчисляем показатели обслуживания многоканальной СМО: 1. Интенсивность нагрузки: Интенсивность нагрузки ρ=0.923 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 2. Время обслуживания: Поскольку 0.923<4, то процесс обслуживания будет стабилен. 3. Вероятность, что канал свободен (доля времени простоя каналов): Следовательно, 39.7% в течение часа канал будет не занят, время простоя равно tпр = 23.8 мин. 4. Вероятность отказа (Доля заявок, получивших отказ). Поскольку отказ в обслуживании в таких системах не может быть, то pотк = 0. 5. Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен). Относительная пропускная способность: Q = pобс = 1. 6. Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов): nз = ρ = 0.923 канала. Среднее число простаивающих каналов: nпр = n - nз = 4 - 0.923 = 3.1 канала. 7. Коэффициент занятости каналов обслуживанием: Следовательно, система на 20% занята обслуживанием. 8. Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок): A = λ = 12 заявок/час. 9. Среднее время простоя СМО: tпр = pотк • tобс = 0 • 0.0769 = 0 час. Вероятность образования очереди: Вероятность отсутствия очереди: p = 1 - pоч = 1 - 0.0036 = 0.996 Вероятность того, что придется ждать начала обслуживания равна вероятности того, что все каналы заняты: 10. Среднее число заявок, находящихся в очереди: 11. Среднее время простоя СМО (среднее время ожидания обслуживания заявки в очереди): 12. Среднее число обслуживаемых заявок: Lоб = ρ = 0.923 13. Среднее число заявок в системе: LCMO = Lоч + Lобс = 0.00468 + 0.923 = 0.928 ед. 14. Среднее время пребывания заявки в СМО: Число заявок, получивших отказ в течение часа: λ • p1 = 0 заявок в час. Номинальная производительность СМО: 4 / 0.0769 = 52 заявок в час. Фактическая производительность СМО: 12 / 52 = 23% от номинальной производительности. 2. Построим модель многоканальной системы массового обслуживания с ограниченной очередью. Система может находиться в одном из состояний S0, S1, S2,…, Sk,…, Sn,…, — нумеруемых по числу заявок, находящихся в СМО: S0 — в системе нет заявок (все каналы свободны); S1 — занят один канал, остальные свободны; S2 — заняты два канала, остальные свободны;..., Sk — занято k каналов, остальные свободны;..., Sn — заняты все n каналов (очереди нет); Sn+1 — заняты все n каналов, в очереди одна заявка;..., Sn+r — заняты все n каналов, r заявок стоит в очереди. 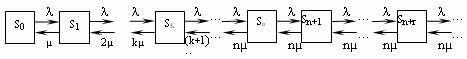 Исчисляем показатели обслуживания многоканальной СМО. 1. Интенсивность нагрузки: Интенсивность нагрузки ρ=0.923 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания. 2. Время обслуживания: Поскольку 0.923<4, то процесс обслуживания будет стабилен. 3. Вероятность, что канал свободен (доля времени простоя каналов). Следовательно, 39.7% в течение часа канал будет не занят, время простоя равно tпр = 23.8 мин. Вероятность того, что обслуживанием: - занят 1 канал: p1 = ρ1/1! p0 = 0.9231/1! • 0.397 = 0.366 - заняты 2 канала: p2 = ρ2/2! p0 = 0.9232/2! • 0.397 = 0.169 - заняты 3 канала: p3 = ρ3/3! p0 = 0.9233/3! • 0.397 = 0.052 - заняты 4 канала: p4 = ρ4/4! p0 = 0.9234/4! • 0.397 = 0.012 4. Вероятность отказа (Доля заявок, получивших отказ): Заявки не получают отказ. Обслуживаются все поступившие заявки. 5. Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен). В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: pотк + pобс = 1 Относительная пропускная способность: Q = pобс. pобс = 1 - pотк = 1 - 0.000148 = 1 Следовательно, 100% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%. 6. Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов): nз = ρ • pобс = 0.923 • 1 = 0.923 канала. Среднее число простаивающих каналов: nпр = n - nз = 4 - 0.923 = 3.1 канала. 7. Коэффициент занятости каналов обслуживанием: Следовательно, система на 20% занята обслуживанием. 8. Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок). A = pобс • λ = 1 • 12 = 11.998 заявок/час. 9. Среднее время простоя СМО: tпр = pотк • tобс = 0.000148 • 0.0769 = 0 час. Вероятность образования очереди: Вероятность отсутствия очереди: p = 1 - pоч = 1 - 0.0154 = 0.985 10. Среднее число заявок, находящихся в очереди: 11. Среднее время простоя СМО (среднее время ожидания обслуживания заявки в очереди): 12. Среднее число обслуживаемых заявок: Lобс = ρ • Q = 0.923 • 1 = 0.923 ед. 13. Среднее число заявок в системе: LCMO = Lоч + Lобс = 0.00449 + 0.923 = 0.927 ед. 14. Среднее время пребывания заявки в СМО: Число заявок, получивших отказ в течение часа: λ • p1 = 0.00178 заявок в час. Номинальная производительность СМО: 4 / 0.0769 = 52 заявок в час. Фактическая производительность СМО: 11.998 / 52 = 23% от номинальной производительности. |