Контрольную работу (стр. 29)
 Скачать 249.77 Kb. Скачать 249.77 Kb.
|
Формула БайесаПусть событиеА может наступить лишь при условии появления одного из несовместных событий (гипотез)H1,H2, …,Hn, которые образуют полную группу событий. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формулам Байеса 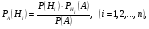 где 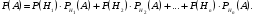 Формула БернуллиВероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления событияравна p(0 < p< 1), событие наступит ровноmраз (безразлично,в какой последовательности), равна 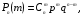 где где 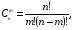 q= 1 – p. q= 1 – p.Вероятность того, что в n испытаниях событие наступит: а)менееm раз; б) болееm раз; в) не менееm раз; г) не болееm раз, находят соответственно по формулам: Pn(0) + Pn(1) +…+ Pn(m– 1); Pn(m+ 1) + Pn(m+ 2) +…+ Pn(n); Pn(m) + Pn(m + 1) +…+ Pn(n); Pn(0) + Pn(1) +…+ Pn(m). Формула ПуассонаЕсливероятность pнаступления события A – постоянна и мала, а число испытаний n – велико и число λ = np – незначительно (будем полагать, что λ = np≤ 10), то имеет место приближенное равенство: 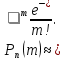 Локальная и интегральная теорема Муавра-ЛапласаЛокальная теорема.Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р <1), событие наступит ровно m раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n) 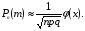 Здесь 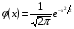 , , 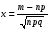 , ,Таблица значений функции Гаусса 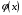 для положительных значений хприведена в приложении 1; для отрицательных значений х пользуются этой же таблицей с учетом того, что функция для положительных значений хприведена в приложении 1; для отрицательных значений х пользуются этой же таблицей с учетом того, что функция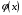 четная, следовательно, четная, следовательно, 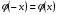 . .Интегральная теорема.Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее m1 раз и не более m2 раз, приближенно равна P(m1; m2) = Φ(x) – Φ(x) Здесь  – функция Лапласа, – функция Лапласа,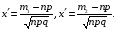 Таблица значений функции Лапласа для положительных значений х(0 ≤ х ≤ 5) приведена в приложении 2; для значений х > 5 полагают Φ(x) = 0,5. Для отрицательных значений х используют эту же таблицу, учитывая, что функция Лапласа нечетная Ф(–x)= –Ф(x). На практике, приближенные равенства из локальной и интегральной теоремы Муавра-Лапласа используют при выполнении условия: npq > 20. Дискретные случайные величиныЗаконом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей. Закон распределения дискретной случайной величины X может быть задан в виде таблицы, первая строка которой содержит возможные значения xi, а вторая – соответствующие вероятности рi:
где 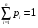 . .Закон распределения дискретной случайнойвеличины X может быть также задан аналитически (в виде формулы): P(X=xi) = φ(xi) или с помощью функции распределения. |
