Контрольную работу (стр. 29)

• Название: Контрольную работу (стр. 29)
• Дата: 14.10.2018
• Размер: 249.77 Kb.
• Имя файла: kontrolnaya_po_TV_i_MS-1.docx
• Тип: Лекции; #53304
• страница: 1 из 16

При изучении курса теории вероятностей и математической статистики студентами заочной формы обучения большая роль отводится самостоятельной работе с учебным материалом. Для проверки приобретения студентами практических навыков им предлагается выполнить внеаудиторную контрольную работу (стр. 29)

Работу над контрольной работой рекомендуется построить следующим образом.

Каждый студент решает свой вариант – его номер в экзаменационной ведомости. В заданиях контрольной работы часто необходимо номер варианта, как переменную N подставить в условие, и решать задачу с рассчитанными по номеру варианта данными; иногда индивидуальные данные для каждого варианта предлагаются в виде таблицы после формулировки текстовой части задания.

Сначала рекомендуется разобрать предложенное решение типовой задачи (стр12);убедиться что при самостоятельном решении этой же задачи получается точно такой же ответ, как в подробном решении. При необходимости следует обращаться к теоретической справке и соответствующей теме в учебниках, перечисленных в списке литературы.

Оформлять контрольную работу необходимо в отдельной тетради в клетку. Обязательно указать фамилию и инициалы, номер варианта. Индивидуальные задания можно решать в любой последовательности.

После проверки контрольной работы преподавателем выставляется оценка «зачтено». При наличии ошибок контрольная работа возвращается на доработку студенту.

ЛЕКЦИИ

Определение вероятности события

Классическое определение вероятности события.При классическом определении вероятность события определяется равенством

P(A)=m/n,

где m – число элементарных исходов испытания, благоприятствующих появлению события A; n – число возможных элементарных исходов испытания. Предполагается, что элементарные исходы образуют полную группу и равновозможны.

Геометрическое определение вероятности. Пусть отрезок lсоставляет часть отрезка L. На отрезке Lнаудачу поставлена случайная точка. Если предположить, что вероятность попадания точки на отрезок lпропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L, то вероятность попадания точки на отрезок lопределяется равенством

P = Длина l/Длина L

Теорема сложения вероятностей

Теорема сложения вероятностей несовместных событий. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р(А + В) = Р(А) + Р(В).

Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р(А₁+А₂+...+А_n) = P(A₁) + Р(А₂) +…+ Р(А_n).

Теорема сложения вероятностей совместных событий.Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления

Р(А+В) = Р(А) + Р(В) – Р(АВ).

Теорема может быть обобщена на любое конечное число совместных событии. Например, для трех совместных событий

Р(A+В+С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(ABC).

Теорема умножения вероятностей

Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Р(АВ) = Р(А)∙Р_A(В).

В частности, для независимых событий

P(АВ) = Р(А)∙Р(В),

т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Формула полной вероятности

Вероятность события А, которое может наступить лишь припоявлении одного из несовместных событий (гипотез)H₁,H₂, …,H_n образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события A: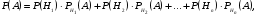



где 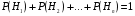.