Контрольную работу (стр. 29)
 Скачать 249.77 Kb. Скачать 249.77 Kb.
|
Формула Бернулли
Решение СобытиеA – родилась девочка. P= P(A) = 0,49; q= 1 – p= 1 – 0,49 = 0,51. Формула Бернулли:  Всего шесть детей, значит n=6. Надо найти вероятность того, что среди них точно одна девочка, значит m= 1. 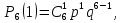 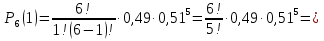  Ответ: 
Решение  Событие A – случайная точка попала на отрезок CB (правее точки C). Так как Cделит ABв отношении 2:1, то: 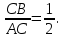 Значит: 2CB=AC; 2CB+CB=AC+CB; 3CB=AB; 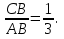 Опираясь на геометрическое определение вероятности, получаем: 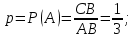  Формула Бернулли:  Всего на отрезокABброшено 6 точек, значит n= 6. Событие B – более одной точки окажется правее точки C. Противоположное событие:  – не более одной точки окажется правее точки C, то есть ни одной точки или ровно одна точка. – не более одной точки окажется правее точки C, то есть ни одной точки или ровно одна точка. 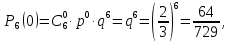  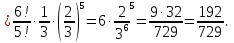 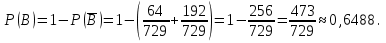 Ответ: 
Решение Событие A – при подбрасывании монеты выпадает герб. 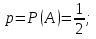 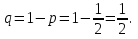 Монета подбрасывается 6 раз, значит n= 6. Событие B – герб выпадет не более 5 раз. Противоположное событие:  – герб выпадет более 5 раз, то есть 6 раз. – герб выпадет более 5 раз, то есть 6 раз. 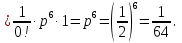  Ответ:  Локальная и интегральная теоремы Муавра-Лапласа. Формула Пуассона
Решение Число испытаний: n= 200. Число появлений события A: m= 70. Вероятность появления события A: p= 0,3, значит q= 1 – p= 0,7. Величина npq= 200∙0,3∙0,7 = 42. Так как npq> 20, то можно воспользоваться приближенным равенством из локальной теоремы Муавра-Лапласа: 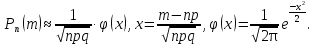 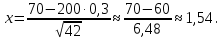 По таблице значений функций Гаусса (приложение 1) находим: 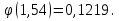 Тогда:  Ответ: 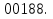
Решение Число испытаний: n= 200. Вероятность появления события A: p= 0,3, значит q= 1 – p=0,7. Величина npq= 200∙0,3∙0,7 = 42. Так как npq> 20, то можно воспользоваться приближенным равенством из интегральной теоремы Муавра-Лапласа: 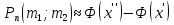 , где , где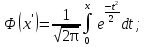 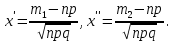 Необходимо найти вероятность того, что событие Aпоявится не более 70 раз, а это значит, что число появлений события Aпринадлежит промежутку [0; 70], то есть m1= 0, m2= 70. 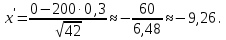 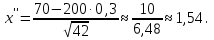 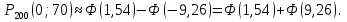 По таблице значений функций Лапласа (приложение 2) находим: 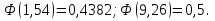  Ответ: 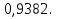
Решение Число испытаний велико: n= 300. Вероятность появления события Aв каждом из них мала: p= 0,01. Произведение λ = np= 300∙0,01 = 3 меньше 10, значит можно искомую вероятность найти по формуле Пуассона: 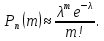 Необходимо найти вероятность того, что событие Aпоявится точно 1 раз, значит m= 1: 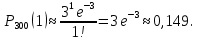 Значение  можно вычислитьв MSExcel, если ввести в любую ячейку формулу =Exp(–3) и нажать Enter. можно вычислитьв MSExcel, если ввести в любую ячейку формулу =Exp(–3) и нажать Enter.Ответ: 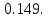 |
