Контрольную работу (стр. 29)

• Название: Контрольную работу (стр. 29)
• Дата: 14.10.2018
• Размер: 249.77 Kb.
• Имя файла: kontrolnaya_po_TV_i_MS-1.docx
• Тип: Лекции; #53304
• страница: 3 из 16

Числовые характеристики дискретных случайных величин

Характеристикой среднего значения случайной величины служит математическое ожидание.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на соответствующие им вероятности:

М(X) = x₁p₁+ x₁p₂+…+ x_np_n.
Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания являются дисперсия и среднее квадратическое отклонение.

Дисперсией случайной величины X называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

D(X) = M[X – M(X)]².

Дисперсию удобно вычислять по формуле

D(Х) = М(X²) – [М(Х)]².

Средним квадратическим отклонением случайной величины называют квадратный корень из дисперсии: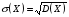

.

Функция распределения

Функцией распределения называют функциюF(x), определяющую для каждого значения х вероятность того, что случайная величина X примет значение, меньшее х, т. е.

F(x) = P(X<x).

Часто вместо термина «функция распределения» используют термин «интегральная функция распределения».

Функция распределения обладает следующими свойствами:

Свойство 1.0 ≤ F(x) ≤ 1.

Свойство 2.Функция распределения – неубывающая функция:

F(х₂) ≥ F(х₁),еслиx₂ > x₁.

Следствие 1. Вероятностьтого, что случайная величинаXпримет значение, заключенное в интервале(a, b)равна приращению функции распределения на этом интервале:

Р(а < X < b) = F(b) – F(а).

Следствие 2.Вероятность того, что непрерывная случайная величина X примет одно определенное значение, например х₁равна нулю:

P(X= x₁)= 0.

Дифференциальная функция распределения

Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения:

f(х) = F(х).

Часто вместо термина «плотность распределения» используют термины «плотность вероятностей» или «дифференциальная функция».

Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a,b),определяется равенством: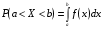

.

Зная плотность распределения, можно найти функцию распределения: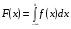

.

Плотность распределения обладает следующими свойствами:

Свойство 1.Плотность распределения неотрицательна, т.е.f(x)≥0.

Свойство 2.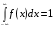. В частности, если все возможные значения случайной величиныпринадлежат интервалу (а, b), то .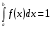

Числовые характеристики непрерывных случайных величин

Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ox, определяется равенством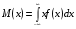

,

гдеf(x) – плотность распределения случайной величины X. Предполагается, что интеграл сходится абсолютно.

В частности, если все возможные значения принадлежат интервалу
(а, b), то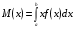

.

Дисперсия непрерывной случайной величины X,возможные значения которой принадлежат всей оси Ох, определяется равенством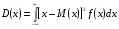

,

или равносильным равенством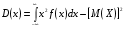

.

В частности, если все возможные значения X принадлежат интервалу (a, b), то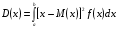

.
Среднее квадратическое отклонение непрерывной случайной величины определяется так же, как и для дискретной величины: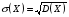

_.