Контрольную работу (стр. 29)
 Скачать 249.77 Kb. Скачать 249.77 Kb.
|
Формула полной вероятности. Формула Байеса
Решение СобытиеA – достали черный шар. Событие Aможет произойти с одним из несовместных событий (гипотез): H1 – шар достали из первой урны; H2 – шар достали из второй урны; H3 – шар достали из третьей урны. Так как урны с виду одинаковы, то: 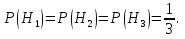 Найдем условные вероятности события Aдля каждой гипотезы. Черный шар достали из первой урны: 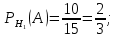 Аналогично: 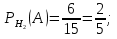 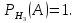 По формуле полной вероятности: 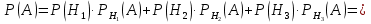 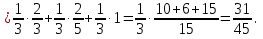 Ответ: 
Решение СобытиеA – из второй урныдостали черный шар. Событие Aможет произойти с одним из несовместных событий (гипотез): H1 – из первой урны во вторую переложили белый шар; H2 – из первой урны во вторую переложили черный шар. Вероятности гипотез: 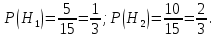 Найдем условные вероятности события A. Если из первой урны во вторую переложили белый шар, то во второй урне стало 10 белых и 6 черных шаров. Значит, вероятность достать из нее черный шар равна: 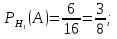 Аналогично: 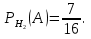 По формуле полной вероятности: 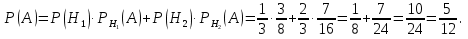 Ответ: 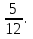
Решение СобытиеA – из наугад выбранной урны достали один шар. Событие Aможет произойти с одним из несовместных событий (гипотез): H1 – шар достали из первой урны; H2 – шар достали из второй урны; H3 – шар достали из третьей урны. Априорные вероятности гипотез равны: 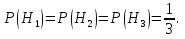 В задаче 4 найдены условные вероятности события Aи его полная вероятность: 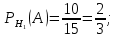 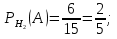 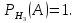 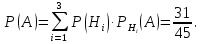 Найдем по формуле Байеса апостериорную вероятность гипотезы H2. Черный шар достали из второй урны: 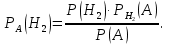 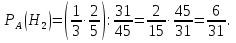 Сравним 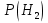 и и 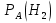 : :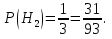 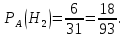 Таким образом, если известно, что достали черный шар, то вероятность того, что его достали из второй урны уменьшается (это соответствует условию – во второй урне меньше всего черных шаров). Ответ: 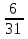 . . |
