Контрольную работу (стр. 29)

• Название: Контрольную работу (стр. 29)
• Дата: 14.10.2018
• Размер: 249.77 Kb.
• Имя файла: kontrolnaya_po_TV_i_MS-1.docx
• Тип: Лекции; #53304
• страница: 8 из 16

Дискретные случайные величины

13. 
    В денежной лотерее выпущено 100 билетов. Разыгрывается четыре выигрыша по 5 тысяч рублей; пять выигрышей по 4 тысячи рублей и одиннадцать выигрышей по 1 тысячи рублей.
    

1. 
   Составить ряд распределения случайной величины X – размер выигрыша по одному купленному билету.
   
2. 
   Найти математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины.
   
3. 
   Записать функцию распределения и построить ее график.
   

Решение

а) Случайная величина X – размер выигрыша по одному купленному билету.

Возможные значения случайной величины:

0; 1; 4; 5.

Вероятность выиграть 5 тысяч рублей по одному билету: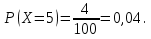



Аналогично определяются вероятности остальных значений случайной величины.

Ряд распределения имеет вид:

X	0	1	4	5
p	0,8	0,11	0,05	0,04

б) Найдем числовые характеристики случайной величины.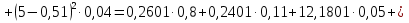


















в) Найдем функцию распределения случайной величины F(x).

По определению: F(x) = P(X< x).

1) Пусть x= 0, найдем F(x):

F(0) = P(X< 0),

то есть вероятность того, что выигрыш по лотерейному билету будет меньше нуля, но это невозможное событие, значит P(X< 0) = 0 и F(0) = 0.

Очевидно, что для всех чисел из промежутка (–∞; 0] значение функции распределения будет таким же:

x ≤ 0: F(x) = 0.

2) Пусть x= 1, найдем F(x):

F(1) = P(X< 1),

то есть вероятность того, что выигрыш по лотерейному билету будет меньше 1, т.е. выигрыш будет равен нулю:

F(1) = P(X< 1) = P(X= 0) = 0,8.

Очевидно, что для всех чисел из промежутка (0; 1] значение функции распределения будет таким же:

0 < x ≤ 1: F(x) = 0,8.

3) Пусть x= 4, найдем F(x):

F(4) = P(X< 4),

то есть вероятность того, что выигрыш по лотерейному билету будет меньше 4, значит выигрыш равен нулю или равен 1т.р.:

F(4) = P(X< 4) = P(X= 0) + P(X= 1) = 0,8 + 0,11 = 0,91.

Очевидно, что для всех чисел из промежутка (1; 4] значение функции распределения будет таким же:

1 < x ≤ 4: F(x) = 0,91.

4) Пусть x= 5, найдем F(x):

F(5) = P(X< 5),

то есть вероятность того, что выигрыш по лотерейному билету будет меньше 5, значитравен нулю или 1 т.р. или 4т.р.:

F(5) = P(X< 5) = P(X= 0) + P(X= 1) + P(X= 4) =

= 0,8 + 0,11 + 0,05 = 0,96.

Очевидно, что для всех чисел из промежутка (4; 5] значение функции распределения будет таким же:

4 < x ≤ 5: F(x) = 0,96.

5) Пусть x> 5,например,x= 6;найдем F(x):

F(6) = P(X< 6),

то есть вероятность того, что выигрыш по лотерейному билету будет меньше 6, а это достоверное событие – в любом случае выигрыш будет меньше 6 т.р. (возможные значения 0; 1; 4; 5), поэтому:

F(6) = 1.

Очевидно, что для всех чисел больших 5, то есть из промежутка (5; +∞)значение функции распределения будет таким же:

x > 5: F(x) = 1.

Получаем:



Построим ее график: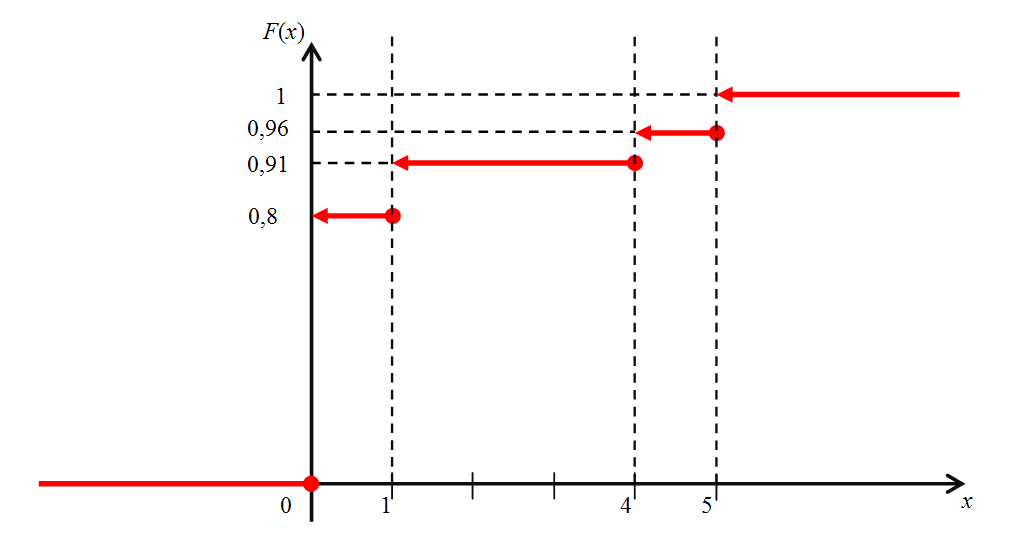


Ответ: