Контрольную работу (стр. 29)
 Скачать 249.77 Kb. Скачать 249.77 Kb.
|
Числовые характеристики вариационных рядовВыборочное среднее 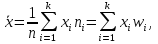 где  – варианты дискретного ряда или середины интервалов интервального ряда; – варианты дискретного ряда или середины интервалов интервального ряда;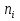 – частоты вариант или интервалов; – частоты вариант или интервалов; – частости вариант или интервалов. – частости вариант или интервалов.Средняя отклонений вариантов от средней равна нулю:  Медианой (Md) вариационного ряда называется значение признака, приходящегося на середину ранжированного ряда наблюдений. Для дискретного вариационного ряда с нечетным числом членов медиана равна серединному варианту, а для ряда с четным числом членов – полусумме двух серединных вариантов. Для интервального вариационного ряда: 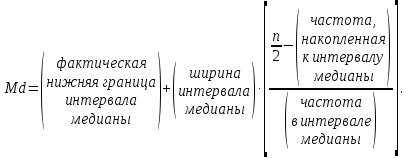 Модой (Mo) вариационного ряда называется варианта, которой соответствует наибольшая частота. Для дискретного вариационного ряда мода находится по определению. Для интервального вариационного ряда: 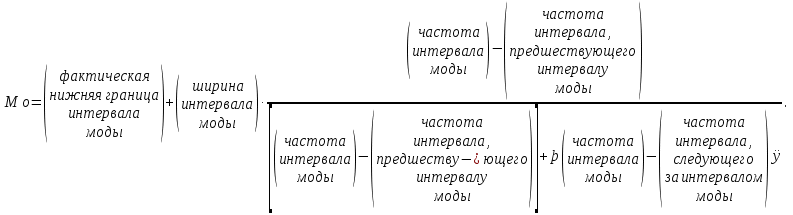 Абсолютные показатели вариации Размах (R) – разность между наибольшим и наименьшим вариантами ряда: 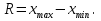 Среднее линейное отклонение (d) – средняя арифметическая абсолютных величин отклонений вариантов от их средней: 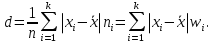 Выборочная дисперсия ( 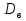 ) – среднее арифметическое квадратов отклонений вариант от их выборочной средней: ) – среднее арифметическое квадратов отклонений вариант от их выборочной средней: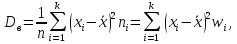 где  – варианты дискретного ряда или середины интервалов интервального ряда. – варианты дискретного ряда или середины интервалов интервального ряда.Для практических вычислений более удобной является формула:  Среднее квадратическое отклонение (стандартное отклонение): 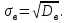 Относительные показатели вариации Коэффициент осцилляции: 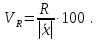 Относительное линейное отклонение:  Коэффициентвариации: 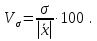 Решение_типовых_задач'>Решение типовых задач Теоремы сложения и умножения вероятностей
а) шары будут одинакового цвета (шары возвращают в урну); б) шары будут разных цветов (шары не возвращают в урну); в) хотя бы один шар будет черным (шары не возвращают в урну). Решение а) Событие A – шары одинакового цвета. Рассмотрим события: A1 = бб – первый шар белый и второй шар белый. Аналогично: A2 = чч – первый шар черный и второй шар черный. Событие Aпроизойдет, если достанут 2 белых или 2 черных шара: A= A1 + A2. 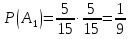 – вероятность достать второй раз белый шар не изменилась, так как шар вернули в урну. Аналогично: – вероятность достать второй раз белый шар не изменилась, так как шар вернули в урну. Аналогично: 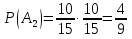 По теореме сложения вероятностей для несовместных событий A1и A2: 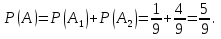 б) Событие B – шары разных цветов. Рассмотрим события: B1=бч; B2=чб. Ясно, что B= B1 + B2;  – первый шар в урну не вернули, поэтому вероятность – первый шар в урну не вернули, поэтому вероятность 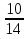 вычислена при условии, что первым достали белый шар. вычислена при условии, что первым достали белый шар.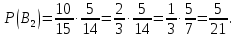 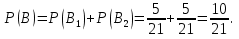 в) Событие C – хотя бы один шар черный. Противоположное событие: 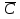 – оба шара белых: – оба шара белых: 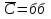 . .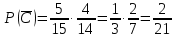 первый шар не вернули в урну, поэтому вероятность первый шар не вернули в урну, поэтому вероятность 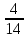 вычислили при условии, что первым достали белый шар. вычислили при условии, что первым достали белый шар.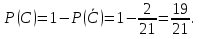 Ответ:а) 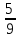 ; б) ; б) 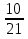 ; в) ; в) 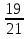 . .
а) третьим по порядку будет вынут черный шар; б) из первых трех шаров хотя бы один шар будет черный. Решение а) Событие A – третьим по порядку будет черный шар. Рассмотрим события: A1 = ббч – первый шар белый, второй шар белый, третий шар черный. Аналогично: A2 = бчч;A3 = чбч;A4 = ччч. Событие Aпроизойдет, если произойдет любое из событий A1, A2, A3, A4: A= A1 + A2 + A3 + A4. Так как из урны последовательно достают все шары, то шары в урну не возвращают и при вычислении вероятности события A1 = ббч рассчитываем условные вероятности того, что второй шар белый (при условии, что первый шар белый) и что третий шар черный (при условии, что первый шар белый и второй шар белый): 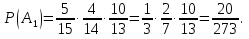 Аналогично: 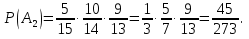  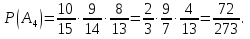 По теореме сложения вероятностей для несовместных событий:  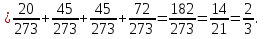 б)Пусть событие B – из первых трех шаров хотя бы один шар будет черным. Противоположное событие:  – все три шара белые: – все три шара белые: 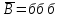 . .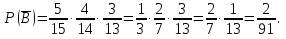 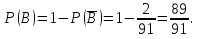 Ответ:а)  ; б) ; б) 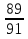 . .
Решение Событие A – по крайней мере два шара одноцветные. Противоположное событие:  – все шара разного цвета. – все шара разного цвета.Рассмотрим события: A1 = бчк – первый шар белый, второй шар черный, третий шар красный. Аналогично: A2=бкч;A3=чбк;A4=чкб;A5=кбч;A6=кчб. СобытиеAпроизойдет, еслипроизойдетлюбоеизсобытийA1, A2, A3, A4, A5, A6: A=A1+A2+A3+A4+A5+A6. Так как шары в урну не возвращают, то при вычислении вероятности события A1=бчк рассчитываем условные вероятности того, что второй шар черный (при условии, что первый шар белый) и что третий шар красный (при условии, что первый шар белый и второй шар черный): 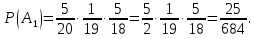 Аналогично: 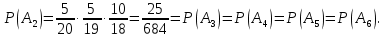 По теореме сложения вероятностей для несовместных событий:  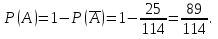 Ответ:  |
