Курсовая. Исследования мотивации учения младших школьников 60%. Краткий обзор психологических особенностей детей младшего школьного возраста 15

• Название: Краткий обзор психологических особенностей детей младшего школьного возраста 15
• Дата: 15.08.2021
• Размер: 1.23 Mb.
• Имя файла: Курсовая. Исследования мотивации учения младших школьников 60%.doc
• Тип: Краткий обзор; #226961
• страница: 11 из 12

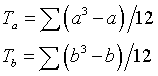где a - объем каждой группы одинаковых рангов в ранговом ряду A;

b - объем каждой группы одинаковых рангов в ранговом ряду B.
Получила: Та= 279.5 ; Тв= 87.5;

3. 
   Сформулировала гипотезы:
   

• 
  H0 - корреляция между высоким уровнем самооценки и уровнем школьной мотивации не отличается от 0;
  
• 
  H1 – корреляция между высоким уровнем самооценки и школьной мотивации отличается от 0.
  

4. 
   Расчитала коэффициент ранговой корреляции rs по формуле (при наличии одинаковых рангов):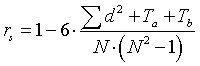
   

где sum(d2) - сумма квадратов разностей между рангами;

Ta и Tb - поправки на одинаковые ранги;

N - количество испытуемых, участвовавших в ранжировании.
П олучила: rs эмп. = 1 - 6 ∙ 6265.25 + 279.5 + 87.5 = 0.42

41 ∙ (41 ∙ 41 - 1)

1. 
   Сравнила значение rs эмпирического со значениями rs критического при (p≤0,05; p≤0,001).
   

rs кр. = 0.31 (p≤0,05); 0.40 ( p≤0,001). Получили: rs эмп. > rs кр.

2. 
   Сформулировала вывод:
   

H0 отвергается. Принимается гипотеза H1 . Корреляция между высоким уровнем самооценки и школьной мотивации значительно отличается от нуля и является статистический значимой. Связь положительная. Следовательно, высокий уровень самооценки повышает уровень школьной мотивации.

Приложение 8
Расчет коэффициента ранговой корреляции Ч.Спирмена rs для установления взаимосвязи высокого уровня интеллекта и уровня школьной мотивации.

1. 
   В сопоставлении будут участвовать два признака как переменные: А – уровень интеллекта и В – уровень школьной мотивации.
   
2. 
   Проранжировала значения переменных A и В, начисляя ранг 1 наименьшему значению, в соответствии с правилами ранжирования. Занесли ранги в третий и пятый столбцы таблицы по порядку номеров испытуемых.
   
3. 
   Подсчитала разности d между рангами A и B по каждой строке таблицы и занесла в шестой столбец таблицы.
   
4. 
   Занесла каждую разность в квадрат: d2. Эти значения занесла в седьмой столбец таблицы. Подсчитала сумму d2.
   

Таблица 11

Расчет коэффициента ранговой корреляции Ч.Спирмена rs для установления взаимосвязи высокого уровня интеллекта и уровня школьной мотивации.

№ п\п		А				В				d		d 2
	Индивид.значения		Ранг		Индивид.значения		Ранг.
1		12		38		10		3.5		34.5		1190.25
2		4		5.5		14		17.5		-12		144
3		12		38		22		24		14		196
4		6		12.5		10		3.5		9		81
5		4		5.5		10		3.5		2		4
6		8		16.5		12		9		7.5		56.25
7		4		5.5		10		3.5		2		4
8		11		31.5		26		36		-4.5		20.25
9		11		31.5		25		30.5		1		1
10		12		38		25		30.5		7.5		56.25
11		10		27		21		22		5		25
12		10		27		25		30.5		-3.5		12.25
13		9		21.5		25		30.5		-9		81
14		4		5.5		14		17.5		-12		144
15		5		11		14		17.5		-6.5		42.35
16		7		14.5		12		9		5.5		30.25
17		9		21.5		10		3.5		18		324
18		9		21.5		28		39		-17.5		306.25
19		4		5.5		12		9		-3.5		12.25
20		9		21.5		25		30.5		-9		81
21		6		12.5		14		17.5		-5		25
22		12		38		13		13		25		625
23		7		14.5		12		9		5.5		30.25
24		4		5.5		13		13		-7.5		56.25
25		4		5.5		12		9		-3.5		12.25
26		9		21.5		24		26		-4.5		20.25

Продолжение таблицы 11

27	9	21.5	26	36	-14.5	210.25
28	10	27	28	39	-12	144
29	12	38	22	24	14	196
30	11	31.5	25	30.5	1	1
31	8	16.5	22	24	-7.5	56.25
32	12	38	28	39	-1	1
33	11	31.5	26	36	-4.5	20.25
34	4	5.5	14	17.5	-12	144
35	4	5.5	14	17.5	-12	144
36	4	5.5	25	30.5	-25	625
37	9	21.5	20	21	0.5	0.25
38	12	38	25	30.5	7.5	56.25
39	11	31.5	10	3.5	28	784
40	11	31.5	13	13	18.5	342.25
41	9	21.5	30	41	-19.5	380.25
						Сумма: 6685

1. 
   Так как имеется наличие одинаковых рангов, то рассчитала поправки по формуле: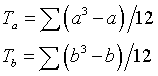
   

где a - объем каждой группы одинаковых рангов в ранговом ряду A;

b - объем каждой группы одинаковых рангов в ранговом ряду B.
Получила: Та= 173.5 ; Тв= 87.5;

5. 
   Сформулировала гипотезы:
   

• 
  H0 - корреляция между высоким уровнем интеллекта и уровнем школьной мотивации не отличается от 0;
  
• 
  H1 – корреляция между высоким уровнем интеллекта и школьной мотивации отличается от 0.
  

6. 
   Расчитала коэффициент ранговой корреляции rs по формуле (при наличии одинаковых рангов):