Курс лекций схемотенхника. Курс лекций схемотехника. Курс лекций по дисциплине Цифровая схемотехника для специальности
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
Арифметические операции над числами с фиксированной точкойСложение (вычитание). Операция вычитания приводится к операции сложения путем преобразования чисел в обратный или дополнительный код. Пусть числа A=>O и В=>О, тогда операция алгебраического сложения выполняется в соответствии с табл. 2.3. Таблица 2.3 Таблица преобразования кодов при алгебраическом сложении
Скобки в представленных выражениях указывают на замену операции вычитания операцией сложения с обратным или дополнительным кодом соответствующего числа. Сложение двоичных чисел осуществляется последовательно, поразрядно в соответствии с табл. 2.2. При выполнении сложения цифр необходимо соблюдать следующие правила. Слагаемые должны иметь одинаковое число разрядов. Для выравнивания разрядной сетки слагаемых можно дописывать незначащие нули слева к целой части числа и незначащие нули справа к дробной части числа. Знаковые разряды чисел участвуют в сложении так же, как и значащие. Необходимые преобразования кодов производятся с изменением знаков чисел. Приписанные незначащие нули изменяют свое значение при преобразованиях по общему правилу. При образовании единицы переноса из старшего знакового разряда, в случае использования ОК, эта единица складывается с младшим числовым разрядом. При использовании ДК единица переноса теряется. Знак результата формируется автоматически, результат представляется в том коде, в котором представлены исходные слагаемые. Пример 4. Сложить два числа А10=7 В10=16 A2=+11=+0111; B2=+1000=+10000. Исходные числа имеют различную разрядность, необходимо провести выравнивание разрядной сетки: [A2]П=[A2]OK=[A2]ДК=0: 00111; [B2]П=[B2]OK=[B2]ДК= 0: 10000. Сложение в обратном или дополнительном коде дает один и тот же результат 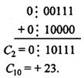 Обратим внимание, что при сложении цифр отсутствуют переносы в знаковый разряд и из знакового разряда, что свидетельствует о получении правильного результата. Пример 5. Сложить два числа А10 = + 16 В10 = —7 в ОК и ДК. В соответствии с табл. 2.3 должна быть реализована зависимость А+(-В), в которой второй член преобразуется с учетом знака 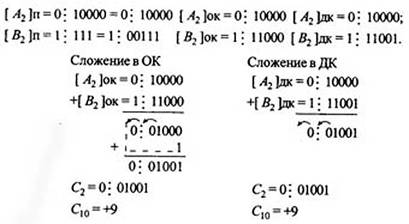 При сложении чисел в ОК и ДК были получены переносы в знаковый разряд и из знакового разряда. В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда (см.п.4 правил). В случае ДК этот перенос игнорируется. Тема 1.4 Основы алгебры логики Логические операции В математической логике определены следующие шесть основных логических операций (связок), которые первоначально были введены еще в классической логике Аристотелем и наиболее часто присутствуют в разнообразных системах программирования: инверсия (логическое отрицание), конъюнкция {логическое произведение), дизъюнкция (нестрогое логическое сложение), исключающая дизъюнкция (строгое логическое сложение), импликация (логическое следствие), эквиваленция. Для обозначения этих логических операций применяются следующие символические обозначения (здесь приведены различные обозначения, встречающиеся в литературе по математической логике и в языках программирования): 1)  , , 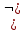 , NOT — обозначает логическое НЕ, , NOT — обозначает логическое НЕ, &., •, AND - обозначает логическое И, &., •, AND - обозначает логическое И,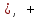 , OR - обозначает логическое ИЛИ, , OR - обозначает логическое ИЛИ,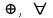 , XOR - обозначает исключающее логическое ИЛИ, , XOR - обозначает исключающее логическое ИЛИ,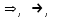 , IMP - обозначает импликацию, , IMP - обозначает импликацию, , EQV - обозначает эквиваленцию. , EQV - обозначает эквиваленцию. Рассмотрим основные логические операции логики высказываний. |
