Курс лекций схемотенхника. Курс лекций схемотехника. Курс лекций по дисциплине Цифровая схемотехника для специальности
 Скачать 0.83 Mb.
|
ОтрицаниеОтрицание - НЕ (иногда ее называют инверсией от inversio - переворачивание, инверсия). Дж. Буль ввел ее как дополнение класса. Отрицание является простейшей логической операцией. Если А - истинное высказывание, то высказывание 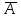 является ложным высказыванием, и наоборот, если А ложно, то 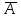- истинно. Логическое отрицание выражается словосочетанием «неверно, что» или просто "не". Например, высказывание «Число 7 делится нацело на 4» является ложным. Отрицанием его будет высказывание «Неверно, что число 7 делится нацело на 4», которое становится истинным. Операция логического отрицания наглядно определяется следующей таблицей, называемой таблицей истинности операции {матрицей истинности).
КонъюнкцияКонъюнкция (логическое произведение, от conjunctio - связывать). Дж. Буль ввел се как умножение классов. Конъюнкция является простейшей логической операцией и соответствует союзу «И». Например, если заданы два высказывания А и В, то их конъюнкция будет А и В. При выражении конъю    нкции используются и другие словосочетания. Например, как А, так и В; не только А , но и В, а также и другие словосочетания, в которых требуется одновременное выполнение высказываний А и В. Вместо союза «И» используются также союзы «НО», "ХОТЯ". Конъюнктивное высказывание А и В - это высказывание, в котором утверждается наличие двух ситуаций. Например, если есть высказывания А - "Солнце светит" и В - "Нет дождя", то конъюнкция высказываний А и В будет "Солнце светит и нет дождя" или "Солнце светит, а дождь не идет". Операция конъюнкции определяется с помощью следующей таблицы истинности.
Сложное высказывание А  В истинно в том и только том случае, когда оба высказывания А и В являются истинными. Например, пусть имеем высказывание А – «число 100 делится на 5» и высказывание В – «число 100 больше числа 5». Тогда сложное высказывание А В будет истинным, так как оба высказывания истинны. Понятию конъюнкции в математике соответствует понятие системы - если заданы, например, два уравнения f1(x) = 0 и f2(x) = 0то система уравнений f  1(x) = 0 f2(x) = 0 будет иметь решения х, при которых выполняются (истинны) одновременно оба уравнения Систему уравнений в математической литературе иногда вместо фигурных скобок так и обозначают с использованием знака конъюнкции - (&)f1(x)=0 f2(x)=0. |