Курс лекций схемотенхника. Курс лекций схемотехника. Курс лекций по дисциплине Цифровая схемотехника для специальности
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
ИмпликацияИмпликация (логическое следование, от implicatio — тесно связывать) является также простейшей логической операций логики высказываний. Эта операций в классической логике выражается словосочетанием «Если . ., то или «В необходимо для А»; «А достаточно для В». Импликация обозначается А  В или А В или А  В. По определению импликация А В. По определению импликация А В истинна всегда, за исключением случая, когда А истинно, а В ложно. Таблица истинности для импликации имеет следующий вид: В истинна всегда, за исключением случая, когда А истинно, а В ложно. Таблица истинности для импликации имеет следующий вид:
Из первых двух строчек таблицы следует, обычно использующееся в классической логике, утверждение "из лжи можно вывести все что угодно", то сеть получить как истинное, так и ложное высказывание. Например, А) Если 2 + 3 = 1, то 2  2 = 4. 2 = 4. Б) Если 2+ 3=4, то 2  2 = 5. 2 = 5.Очень часто высказывание, стоящее после слова "Если", называется основанием или посылкой, а стоящее после слова "то", называется следствием или заключением. Например, "Если идет дождь, то земля мокрая". Здесь простое высказывание "идет дождь" – основание, а следствие - "земля мокрая''. ЭквиваленцияЭквиваленция (эквивалентность, двойная импликация, от acquivalens — равноценное) является также простейшей логической операцией. Эквиваленция обозначается А 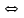 В или А В или А  В. Сложное высказывание А В. Сложное высказывание А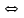 В (читается: А эквивалентно В) истинно тогда и только тогда, когда А истинно и В истинно либо А ложно и В ложно. В остальных случаях А В (читается: А эквивалентно В) истинно тогда и только тогда, когда А истинно и В истинно либо А ложно и В ложно. В остальных случаях А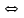 В ложно. Эквиваленция задается следующей таблицей истинности. В ложно. Эквиваленция задается следующей таблицей истинности.
Таким образом, сложное высказывание А 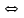 В - это высказывание, в котором утверждается одновременно наличие или отсутствие ситуаций А и В. В классической логике и на естественном языке эквиваленция выражается словосочетаниями: «Если и только если . . , то . .» , «В том и только в том случае, когда. . , то . .» «Тогда и только тогда, когда ..». "Тогда и только тогда когда, А необходимо и достаточно для В". В соответствии с определением эквиваленции как двойной импликации, ее можно представить как конъюкцию двух импликаций: из А следует В, а из В следует А В - это высказывание, в котором утверждается одновременно наличие или отсутствие ситуаций А и В. В классической логике и на естественном языке эквиваленция выражается словосочетаниями: «Если и только если . . , то . .» , «В том и только в том случае, когда. . , то . .» «Тогда и только тогда, когда ..». "Тогда и только тогда когда, А необходимо и достаточно для В". В соответствии с определением эквиваленции как двойной импликации, ее можно представить как конъюкцию двух импликаций: из А следует В, а из В следует А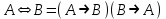 Если сравнить приведенные таблицы истинности для эквиваленции и исключающей дизъюнкции, то видно, что одна является инверсией другой (исключающее ИЛИ есть инверсия эквиваленции и наоборот). Поэтому часто логическую связку исключающее ИЛИ так и называют неэквивалентность. Некоторые простейшие логические операции не являются независимыми, они могут быть выражены через систему других простейших логических операций. Например, А  В = В =  , то есть эквиваленция может быть выражена через строгую дизъюнкцию и отрицание. В свою очередь логическая операция исключающей дизъюнкции может быть выражена также через операции конъюнкции, дизъюнкции и отрицания следующим образом: , то есть эквиваленция может быть выражена через строгую дизъюнкцию и отрицание. В свою очередь логическая операция исключающей дизъюнкции может быть выражена также через операции конъюнкции, дизъюнкции и отрицания следующим образом: Как видим, все логические операции, за исключением операции отрицания, являются бинарными или двухместным» операциями, в которых обязательно присутствуют два операнда, а операция отрицания является унарной или одноместной логической операцией, которая действует на одно логическое высказывание или операнд. 2. Логические функции С помощью логических операции и логических переменных можно составить различные логические функции. Логические функции от любого количества логических переменных часто называют двоичными функциями (Булевыми функциями), так как при любом допустимом наборе логических переменных логические функции принимают только два значения - истина или ложь (1 или 0). Каждая логическая переменная также может принимать только два значения - истина или ложь (1 или 0). Логические переменные иногда называют пропозиционными переменными {от propositio - предложение, высказывание). Кроме высказываний и логических операций в алгебре высказываний рассматриваются логические константы. Таких логических констант две - 1 и 0. Они отождествляются с абсолютной истиной и абсолютной ложью. Введенных в рассмотрение логических операций вполне достаточно для того, чтобы из простейших высказываний образовывать любые сложные высказывания. Зная таблицы истинности логических операции, можно построить таблицу истинности для любого сложного высказывания. Примерами составных высказываний могут быть следующие высказывания:  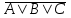  Приведенные выше высказывания называются формулами алгебры высказываний. Эти формулы состоят из простых высказываний А, В, знаков логических операций (  ), а также скобок. Скобки, как и в обычной алгебре, указывают последовательность выполнения логических операций. При отсутствии скобок все логические операции выполняются в зависимости от их приоритетности. Иногда вместо приоритетности в алгебре логики говорят о "связывании" логических операций: первой всегда выполняется операция отрицания, затем конъюнкция, дизъюнкция, исключающая дизъюнкция, импликация и эквиваленция. Все введенные выше логические операции приведены в порядке приоритета. Например, по приоритету конъюнкция выполняется раньше дизъюнкции. В этом случае говорят, что конъюнкция связывает сильнее, чем дизъюнкция. ), а также скобок. Скобки, как и в обычной алгебре, указывают последовательность выполнения логических операций. При отсутствии скобок все логические операции выполняются в зависимости от их приоритетности. Иногда вместо приоритетности в алгебре логики говорят о "связывании" логических операций: первой всегда выполняется операция отрицания, затем конъюнкция, дизъюнкция, исключающая дизъюнкция, импликация и эквиваленция. Все введенные выше логические операции приведены в порядке приоритета. Например, по приоритету конъюнкция выполняется раньше дизъюнкции. В этом случае говорят, что конъюнкция связывает сильнее, чем дизъюнкция. |
