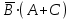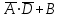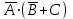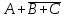Курс лекций схемотенхника. Курс лекций схемотехника. Курс лекций по дисциплине Цифровая схемотехника для специальности
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
Законы идемпотентности.Idempoiens — одинаковость; сохраняющий ту же степень. 1. А + А = А - идемпотентность дизъюнкции 2. А  А = А идемпотентность конъюнкции. А = А идемпотентность конъюнкции.Законы идемпотентности (их еще иногда называют формулами приведения) определяют результат логической операции для двух одинаковых членов. Законы коммутативности. Commutatio - изменение, перемена. 3. A + В = В + А - коммутативность дизъюнкции. 31 А  В = В В = В  А – коммутативность строгой дизъюнкции. А – коммутативность строгой дизъюнкции.4. А  В = В • А - коммутативность конъюнкции В = В • А - коммутативность конъюнкции5. А  В = В В = В  А - коммутативность эквиваленции. А - коммутативность эквиваленции. Законы коммутативности (переместительиые законы) утверждают, что для операций логического сложения, строгого логического сложения, умножения и эквиваленции безразлично в каком порядке записываются высказывания. Законы ассоциативности Associatio- соединение. 6. 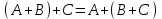 - ассоциативность дизъюнкции - ассоциативность дизъюнкции7. 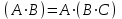 - ассоциативность конъюнкции. - ассоциативность конъюнкции.8. (А  В) В)  С = А С = А (В (В С) - ассоциативность эквиваленции. С) - ассоциативность эквиваленции. Законы ассоциативности (сочетательные законы) утверждают, что при выполнении операций логического сложения, умножения или эквиваленции безразличен порядок их выполнения. Дистрибутивные законы Distribution- размещение, распределение 9. А • (В + С) = (А • В) + (А  С) - 1 дистрибутивный закон. С) - 1 дистрибутивный закон.10. А + (В• С) = (А + В)  (А + С) – 2 дистрибутивный закон. (А + С) – 2 дистрибутивный закон.Дистрибутивные законы (распределительные законы) определяют порядок преобразований сложных логических операций. Одинаковые логические переменные в дизъюнкции и конъюнкции можно выносить за скобки. 1 дистрибутивный закон называется также распределением конъюнкции по дизъюнкции. 2дистрибутивный закон, в отличие от предыдущего, не имеет аналога в алгебре и применяется только для логических переменных и функций. 2 дистрибутивный закон называется также распределением дизъюнкции по конъюнкции. Законы инфолюции. 11. 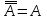 - закон двойного отрицания. - закон двойного отрицания.Закон двойного отрицания утверждает, что двойное отрицание некоторого высказывания равносильно этому высказыванию. 12.  13.  Законы де Моргана Законы отрицания - законы инверсии. Inversio- переворачивание. 14.  - первый закон де Моргана. - первый закон де Моргана.15.  - второй закон де Моргана. - второй закон де Моргана.С помощью этих формул конъюнкция может быть выражена через дизъюнкцию с отрицанием и наоборот, дизъюнкция может быть выражена через конъюкцню с отрицанием. Операции с логическими константами. 16. А+1=1 А  1=А 1=А17. А+0=А А  0=0 0=0Операции с переметши и ее инверсией. 18. 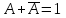 - закон исключенного третьего - закон исключенного третьего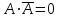 закон непротиворечия (противоречия) закон непротиворечия (противоречия) Применение операции инверсии для логических констант. 19. 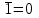 20. 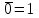 Из законов дистрибутивности и операций с переменной и се инверсией вытекают важные следствия, которые называют формулами расщепления: 21.  - первая формула расщепления - первая формула расщепления22.  - вторая формула расщепления. - вторая формула расщепления.Некоторые из приведенных законов математической лотки аналогичны соответствующим законам арифметики или алгебры и поэтому легко запоминаются. Но некоторые из них не имеют соответствующих аналогов в арифметике и алгебре. Наиболее сильно отличаются от привычных законов алгебры законы идемпотентности, законы инверсии и инфолюции, а также законы, исключающие тождественно истинные и тождественно ложные высказывания, которые определяют работу с логическими константами. Все без исключения законы соответствуют законам над множествами в теории множеств, которые также подчиняются законам булевой алгебры. С помощью аппарата алгебры логики достаточно легко записываются законы классической логики: закон двойного отрицания  , закон исключения третьего , закон исключения третьего  , закон непротиворечия , закон непротиворечия 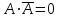 или или 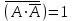 , , закон тождества А = А или А  А = 1 А = 1С помощью аппарата алгебры логики можно записать некоторые принципы, применяемые к логике и теории доказательств. Например, прием доказательство от противного: если утверждение влечет некоторое следствие-утверждение, но не выполняется, то не выполняется и само утверждение. В символах алгебры логики это записывается следующим образом 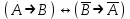 . .Законы логики можно доказать и с помощью таблиц истинности. Доказательство законов де Моргана с помощью таблиц истинности уже было фактически получено в предыдущем примере. Следствия из законов алгебры логики. Из законов алгебры логики вытекают очень важные правила, которые применяются для преобразования и упрощения логических формул. Эти правила преобразовании логических формул называются следствиями алгебры логики. Такими следствиями являются: 23. 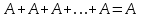 24. 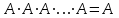 Законы поглощения. 25.  - закон поглощения для конъюнкции. - закон поглощения для конъюнкции.26.  - закон поглощения для дизъюнкции. - закон поглощения для дизъюнкции.Данные законы распространяются на большее количество членов. Например, закон поглощения для дизъюнкции трех переменных может быть записан в следующем виде:  Укажем еще два следствия. 27. 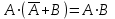 - закон Блейка-Порецкого. - закон Блейка-Порецкого.28. 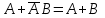 - закон Блсйка-Порецкого. - закон Блсйка-Порецкого.В этих формулах пропадают переменные, входящие с отрицанием относительно внешней переменной в соответствующих конъюнкциях и дизъюнкциях. Формула (27), также как и законы (25) и (26), являются законом поглощения. Формула (28) называют правшам свертки, которое является следствием 2 дистрибутивного закона (10). Докажем формулу (28). Применив к левой части формулы (28) 2 дистрибутивный (распределительный) закон, получим 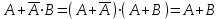 Формулу (27) можно доказать следующим образом: 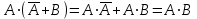 Укажем также важные следствия из законов де Моргана. Отрицание логической суммы нескольких высказываний равно произведению отрицании от каждого из высказываний 29. 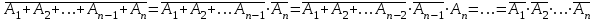 Отрицание логического произведение нескольких высказываний равно сумме отрицаний от каждого из высказываний 30. 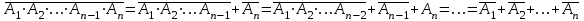 31. 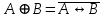 32. 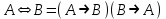 Приведенные равносильности используют Для преобразования логических формул. Рассмотрим несколько примеров. Применение законов алгебры логики Пример 1. С помощью аналитических преобразований в базисе { 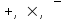 } получить равносильную логическую формулу для исключающей дизъюнкции } получить равносильную логическую формулу для исключающей дизъюнкции 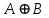 . .Решение. Операция исключающей дизъюнкции является отрицанием эквиваленции. Используя законы инфолюции и законы де Моргана, имеем: 1 способ. по формуле 31 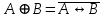 по формуле 13 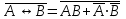 по формуле 14 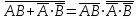 по формуле 15 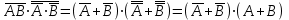 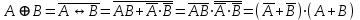 2 способ. 1. по формуле 31 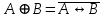 2. по формуле 32 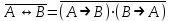 3. по формуле 12 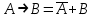 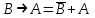 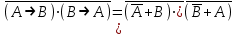 4. по формуле 15 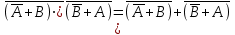 5. по формуле 14 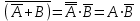 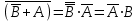 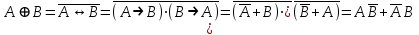 Таким образом, 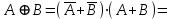 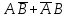 Пример 2. Упростить логическую функцию 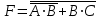 Решение. 1. по формуле 29 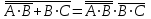 2. по формуле 11 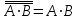 3. по формуле 15 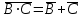 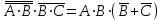 4. по формуле 9 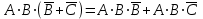 5. по формуле 18 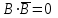 6. 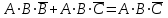  Пример 3 Преобразовать логическую функцию 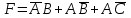 по формуле 11  по формуле 14 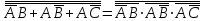 по формуле 15 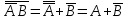 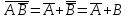 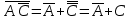 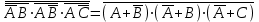 4. 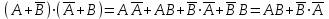 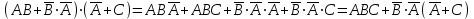 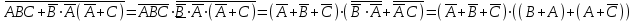 А+А=А А+А=А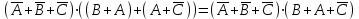 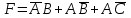 = =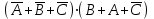 Принцип двойственности Представленные законы (пары: (1) и (2), (3) и (4), (6) и (7), (9) и (10), (14) и (15), (19)# и (20), (21) и (22)) показывают, что между формулами, записанными слева и справа, существует вполне определенная зависимость. Если в любой формуле дизъюнкцию заменить конъюнкцией, конъюнкцию заменить дизъюнкцией, 0 заменить 1,1 заменить 0, а отрицание сохранить без изменения, то формула с нечетным номером (например, (9) перейдет в формулу с четким номером (10), и наоборот). Значит, с помощью указанных замен можно из одних равносильностей получить другие. Эта закономерность называется законом или принципом двойственности. Этот закон справедлив вообще для всех формул алгебры логики. Дело в том, что приведенных равносильностей вполне достаточно, чтобы с их помощью доказать любую другую равносильность. Поэтому установленная закономерность сохраняется и по отношению к любым другим равносильностям, если только соответствующие формулы не содержат импликацию. В связи с этим говорят, что операция конъюнкции двойственна операции дизъюнкции и наоборот, а формулы F1и F2называют двойственными, если одна получается из другой, как указано выше, заменой каждой операции на двойственную операцию. Иллюстрацией сказанного является следующий пример. Пример. Дана формула 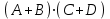 . Получить двойственную ей формулу. . Получить двойственную ей формулу.Решение. Преобразуем исходную формулу в равносильную.  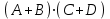 = =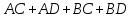 Составим теперь двойственную равносильность 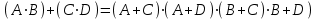 Эту равносильность можно доказать с помощью формулы (10). Обобщая вышеприведенное правило получения двойственной формулы, в математической логике доказано, что если есть некоторая формула F(A,B,...,Z) и к ней двойственна логическая формула Ф(А,В,...Z) то они удовлетворяют тождествам 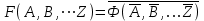 или или 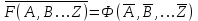 . .Эти соотношения используют при преобразовании логических формуя и называют правилам отрицания, которое дополняет следствия алгебры логики. Справедлив также принцип двойственности; Если две логические формулы F1(A,B,...,Z) и F2(A,B,...,Z) равносильны, то сеть F1(A,B,...,Z) = F2(A,B,...,Z) и каждая из них имеет двойственную формулу Ф1(A,B,...,Z) и Ф2(A,B,...,Z), то равносильны и двойственные формулы F1(A,B,...,Z) = F2(A,B,...,Z) Тема 1.6 Переключательные функции Переключательные функции В логике не требуется знания абсолютного значения величины, поэтому физическая величина, подвергаемая логическим преобразованиям, называется переменной, или аргументом, и представляется ее положительная (Н) или менее положительная (L). Этим Значениям, называемым логическими уровнями, условно приравнивая значения 1 и 0, или наоборот 0 и 1, в зависимости от го соглашения. Логические переменные могут подвергаться различным преобразованиям с использованием логических элементов. Такие преобразования описываются с помощью переключательных функций в которых используются различные буквы латинского алфавита: А, В, С, D, X, Y, x1, x2, хз и т.д. Функция от входных переменных называется переключательной если она так же, как ее аргументы, принимает два значения: лог ческой единице (лог. 1) или логического нуля (лог. 0). Основные базисы. Одна из основных задач синтеза заключается в выборе типов элементов, на которых будут реализовываться заданные функции. Поэтому необходимо определить минимальный набор логических элементов (базис), образующих функционально полную систему элементов. Базис — это функционально полный набор элементов, с помощью которого можно реализовать сколь угодно сложную переключательную функцию. Их может быть несколько. Базис из логических элементов И, ИЛИ, НЕ называется основным. Пример: Представить логическую функцию в базисе И-НЕ 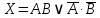 = = 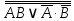 = = 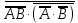 . .Задания для самостоятельной работы Представить заданные логические функции в заданном базисе
|