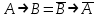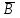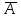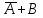Курс лекций схемотенхника. Курс лекций схемотехника. Курс лекций по дисциплине Цифровая схемотехника для специальности
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
Тема 1.5 Законы алгебры логики Законы алгебры логики Как в любой математической дисциплине, в математической логике вводится начальная система аксиом, которой подчиняются все вводимые в ней операции. Такие системы аксиом могут быть различны. Одной из самых простых и естественных систем аксиом в математической логике может быть принята система аксиом, определенная действиями основных логических операций. Все преобразования логических функций производятся формально но правилам вывода: правилу подстановки и правилу заключения. Правило подстановки: Пусть F - истинная формула (тавтология), содержащая переменную А. Тогда, заменив всюду в формуле F букву А другой формулой Ф, получим новую, также истинную, формулу. Из этого правила следует, что если в истинной формуле F можно выделить какую-либо подформулу, которая может быть заменена другим тождественным выражением, то, сделав такую замену, получим новую истинную формулу. Правило заключения: Если F и F  Ф истинные формулы, то и Ф - истинная формула. Ф истинные формулы, то и Ф - истинная формула.Для того чтобы две логические формулы F1и F2были эквивалентными необходимо и достаточно, чтобы их эквиваленция F1  F2была истинной. Это как раз следует из правила заключения, если вспомнить, что эквиваленция есть двойная импликация, то есть F2была истинной. Это как раз следует из правила заключения, если вспомнить, что эквиваленция есть двойная импликация, то есть F1  F2 =(F1 F2 =(F1  F2 )( F2 F2 )( F2 F1) F1)Из таблицы истинности. Ранее рассмотренного примера следует, что формулы 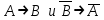 эквивалентны. Тогда их эквиваленция эквивалентны. Тогда их эквиваленция 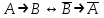 очевидно тождественно-истинна. очевидно тождественно-истинна.
. Смысл этой эквиваленции состоит в том что, доказав утверждение: «Из А следуем В» можно доказать утверждение: «Из отрицания В следует отрицание А». Приведенная эквивалентность, как и в классической логике называется законом контрапозиции. Импликация 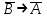 является контрапозицией импликации является контрапозицией импликации 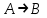 . Эти две формулы в рассуждениях заменяют друг друга. На использовании этой эквивалентности основывается математический метод доказательства от противного. . Эти две формулы в рассуждениях заменяют друг друга. На использовании этой эквивалентности основывается математический метод доказательства от противного.Из совпадения таблиц истинности формул 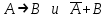 , следует, что эквиваленция , следует, что эквиваленция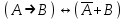 есть тавтология. есть тавтология.
Таким образом, сказать "Из А следует В" - все равно, что сказать "Не А или В". Эквивалентность 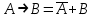 называется законом инфолюции для импликации. называется законом инфолюции для импликации.Очевидно, множество равносильных формул бесконечно. Приведем наиболее важные равносильные формулы, которые используются при преобразованиях формул и которые отражают основные закономерности классической логики. Они называются основными законами алгебры логики.Эти законы, как увидим, аналогичны законам, характеризующим операции над множествами. (Здесь символ = используется для обозначения равносильных формул, то есть формул, которые при одинаковых логических значениях, входящих в них логических переменных, принимают одинаковые логические значения). Если взять любую из этих формул, то эквиваленция левой и правой частей формулы будет тавтологией. Так как возможно представление этих законов через различные базисы, то в дальнейшем будем представлять логические формулы через операции дизъюнкции, конъюнкции и отрицания, то есть систему логических операции{ 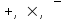 } }Наиболее важными и специфическими из логических законов являются законы идемпотентности,которые исключают все коэффициенты и показатели степеней в логических формулах, содержащих одинаковые выражения. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||