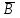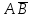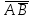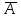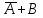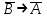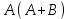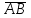Курс лекций схемотенхника. Курс лекций схемотехника. Курс лекций по дисциплине Цифровая схемотехника для специальности
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
Полнота системы логических функцийПолнота системы логических функций. Некоторые введенные простейшие логические операции не являются независимыми, то есть они могут быть выражены с помощью других простейших логических операций. Эти вопросы, как и для любой алгебраической системы, относятся к проблеме так называемой полноты системы логических операций (функций). Система логических функций называется полной, если все остальные логические функции могут быть представлены с помощью подстановок через функции этой выбранной системы. Минимальный набор логических операций, с помощью которых можно представить логические функции, называется базисом или базисной системой. Удаление из базисной системы хотя бы одной операции нарушает свойство полноты системы операции. Система логических функций, использующая для представления всех логических функций только операции логического сложения, логического умножения и отрицания ( 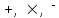 ) является полной, так как любая логическая функция может быть представлена с помощью операций дизъюнкции, конъюнкции и отрицания. Но такая система не является базисной, так как из нее можно исключить операцию дизъюнкции либо конъюнкции и получатся две новые системы, которые также обладают свойством полноты и уже являются ) является полной, так как любая логическая функция может быть представлена с помощью операций дизъюнкции, конъюнкции и отрицания. Но такая система не является базисной, так как из нее можно исключить операцию дизъюнкции либо конъюнкции и получатся две новые системы, которые также обладают свойством полноты и уже являютсябазисными. Эти два базиса так и называют — конъюнктивный базис – { 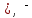 } и } идизъюнктивный базис - {+,  }. }.Оказывается, что существуют такие единичные логические операции, которые обладают свойством полноты и являются базисными, то есть с помощью одной такой логической операции можно выразить все остальные логические операции, а, следовательно, и все логические функции. Таким свойством обладают две элементарные бинарные логические операции: отрицание конъюнкции {антиконъюнкция) и отрицание дизъюнкции (антидизъюнкция), которые также часто называют по имени ученых-логиков, соответственно, штрих Шеффера (|) и строка Пирса — ( 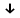 ). Логические операции штрих Шеффера (|) и стрелка Пирса ( ). Логические операции штрих Шеффера (|) и стрелка Пирса (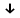 ) определяются следующим образом. ) определяются следующим образом.Отрицание от конъюнкции Отрицание от конъюнкции (отрицание от логического умножения, антиконъюнкция) является операцией от двух логических переменных, которая принимает нулевое значение при единичных значениях переменных. Эту логическую операцию называют функцией Шеффера (штрих Шеффера) и ее обозначают А|В (читается: А штрих Шеффера В). Штрих Шеффера эквивалентен. А|В= 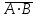 = =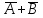 Операция штрих Шеффера – А|В задается следующей таблицей истинности.
Отрицание от дизъюнкции Отрицание от дизъюнкции (отрицание от логического сложения, антидизъюнкция) является операцией от двух логических переменных, которая принимает единичное значение при нулевых значениях переменных. Эту логическую операцию также называется функцией Пирса (стрелка Пирса) и обозначают А 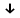 В (читается "А стрелка Пирса В"). Стрелка Пирса эквивалентна A В (читается "А стрелка Пирса В"). Стрелка Пирса эквивалентна A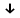 B= B=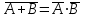 Иногда эту операцию называют НИ-НИ - "неправильно, что А и неправильно, что В"). Операция стрелка Пирса - A 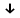 В задается следующей таблицей истинности В задается следующей таблицей истинности
Сводная таблица истинности элементарных логических операции
Запись различных высказываний на естественном языке с помощью аппарата алгебры логики Аппарат математической логики можно с успехом использовать для решения логических содержательных задач, отличающихся сложностью и запутанностью исходных данных. При решении таких задач с помощью рассуждений паши высказывания не могут до конца выразить всю полноту мысли и не обладают достаточной ясностью. Поэтому, если предварительно перевести все высказывания в символику алгебры логики, а затем использовать аппарат этой алгебры, то можно получить четкое решение задачи с однозначным ответом. Ясно, что при решении таких задач, кроме знания самих элементарных логических операций, необходимо умение записывать высказывания, приведенные на естественном языке, с помощью символического языка алгебры логики. Напомним еще раз» что различают два вида высказывании: простые и сложные. Простые высказывания надо рассматривать как не членимые на части логические объекты. Из простых высказываний можно составить сложные высказывания. Сложное высказывание состоит из двух или более простых высказываний. соединенных с помощью логических операций. Логическое значение сложного высказывания зависит от истинностных значении составляющих его простых высказываний и его структуры. Рассмотрим несколько примеров записи высказываний на естественном языке с помощью аппарата алгебры логики. Пример 1 Записать на языке алгебры логики следующее высказывание: "Для солнечной погоды достаточно, чтобы не было ни ветра, ни дождя". Решение. Введем следующие простые высказывания: С- солнечная погода. В - дует ветер, D - идет дождь. Тогда приведенное высказывание будет записано как 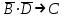 Пример 2 Записать на языке алгебры логики следующее высказывание: «Я поеду и Москву и если встречу там друзей, то мы интересно проведем время» Решение. Введем следующие простые высказывания М - я поеду в Москву; В - встречу там друзей; И - интересно проведем там время. Тогда 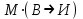 Пример 3 Записать на языке алгебры логики следующее высказывание: "Если я поеду в Москву и встречу там друзей, то мы интересно проведем время". Решение. Введем следующие простые высказывания: М - я поеду в Москву; В - встречу там друзей; И - интересно проведем там время. Тогда 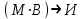 Пример 4 Записать на языке алгебры логики следующее высказывание: "Неверно, что если дует ветер, то солнце светит только тогда, когда нет дождя". Решение. Введем следующие простые высказывания: В - дует ветер; D - идет дождь; С - светит солнце. Исходное высказывание на языке алгебры логики имеет вид: 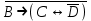 Пример 5 Записать на языке алгебры логики следующее высказывание: "Если будет солнечная погода, то ребята пойдут в лес, а если будет пасмурная погода, то ребята пойдут в кино". Решение. Введем следующие простые высказывания: С - будет солнечная погона; L - ребята пойдут в лес; К- ребята пойдут в кино. 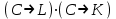 Пример 6 Записать на языке алгебры логики следующее высказывание: "Неверно, что если погода пасмурная, то дождь идет тогда и только тогда, когда нет ветра". Решение. Введем следующие простые высказывания: Р - будет пасмурная погода; D - идет дождь; В - дуст ветер. 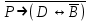 Пример 7 Записать на языке алгебры логики следующее высказывание: "Если не будет экономического кризиса, то достаточным условием стабильности курса рубля будет отсутствие политического кризиса в стране". Решение. Введем следующие высказывания: ЕК - будет экономический кризис, SR - будет стабильность курса рубля, PC - будет политический кризис. Тогда 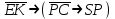 Пример 8 Записать на языке алгебры логики следующее высказывание: "Эффективную финансовую политику предприятия можно ожидать, если будет экономическая стабильность в обществе". Решение. Введем высказывания: F- будет эффективная финансовая политика, S - будет экономическая стабильность в обществе. Тогда 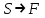 ЗАДАЧИ И УПРАЖНЕНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 1. Пусть заданы следующие два простейших высказывания: В - дует ветер, и D- идет дождь. Что означают на естественном языке высказывания 1. 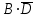 2. 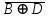 3. 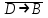 4. 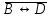 5. 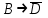 6. 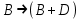 7. 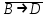 8. 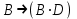 9. 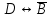 2. Переведите на язык алгебры логики следующее высказывание: "Если для солнечной погоды необходимо отсутствие дождя, то для того, чтобы пошел дождь, достаточно, чтобы погода была пасмурной и безветренной". 3. Переведите на язык алгебры логики следующее высказывание: «Погода будет не только пасмурной, но и дождливой несмотря на ветер. Значит солнечной погоды не будет разве, что прекратится дождь». 4. Пусть заданы следующие три простейших высказывания: В – Билл глуп, D - Джон умен S - Билл не выиграет соревнования. Переведите на естественный язык высказывания, записанные с помощью алгебры высказываний 1. 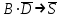 2. 2. 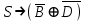 Формулы логики высказываний. Оценка формулы. Отношения между формулами Формулы логики высказываний и понятие логической функции является основными понятиями алгебры высказываний. Формулой языка алгебры логики называется выражение, составленное из высказывательных переменных, логических операций и скобок. Можно дать более точное и более абстрактное определение формулы логики высказываний: 1. Пропозиционная переменная (некоторое высказывание) А и логические константы - 1 и 0 является формулами алгебры высказываний. 2. Если А формула алгебры высказываний, то А являются также формулой. Если А и В являются формулы алгебры высказываний, то формулами алгебры высказывании являются и формулы 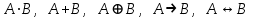 Никаких других формул в логике высказывании нет. Формулы алгебры высказываний, зависящие от некоторого количества логических переменных A1, A2 ,A3,...,An, принято символически обозначать, как и в обычной математике, в виде - F(A1, A2 ,A3,...,An). Каждая формула представляет собой логическую функциювходящих в неe некоторых логических переменных, каждая из которых может принимать только значение 0 или 1. Отметим, что количество различных фиксированных комбинаций, которые может принимать а переменных A1, A2 ,A3,...,An, равно 2п. В дальнейшем понятие формулы алгебры высказываний и двоичной логической функции будем считать эквивалентными, хотя пало сказать, что формул алгебры высказываний составленных из п переменных бесчисленное множество, а число двоичных функций от п переменных конечно и равно 2 . С ростом п число бинарных логических функций резко растет. При п-1 возможно всего 4 функций, при п = 2 число функций равно 16, а при п = 3 и п = 4 уже, соответственно, 256 и 65356. В качестве примера приведем логические функции для случаев одного и двух логических переменных, как наиболее часто встречающихся в практике работы с формулами алгебры логики. Двоичные функции от одной логической переменной
Двоичные функции от двух логических переменных
Некоторые, из приведенных в таблице функций уже рассматривались ранее. Так например, функции F0 и F15 являются тождественно постоянными - F0(A,B) = 0, Fl5(A,B)- 1 (логическими константами). F1(A.B)=AB - является конъюнкцией логических переменных А и В, F7(A,B) = А + В - дизъюнкцией, F9(A, B) = А  В - эквиваленцией, a F13(A,B) = А В - эквиваленцией, a F13(A,B) = А В импликацией. Функции F12, Fl0, F6, F3 и F14 являются, соответственно, отрицанием А, отрицанием В исключающей дизъюнкцией А и В, стрелкой Пирса и штрихом Шеффера. В импликацией. Функции F12, Fl0, F6, F3 и F14 являются, соответственно, отрицанием А, отрицанием В исключающей дизъюнкцией А и В, стрелкой Пирса и штрихом Шеффера.Совокупность фиксированных значений истинности и аргументов A1,A2,A3,....An принято обозначать в виде последовательности нулей и единиц. например 001 …110. Такие последовательности нулей и единиц называют наборами и говорят: что функция F(A*1,A*2,A*3,....A*n) рассматривается на конкретном наборе (A*1,A*2,A*3,....A*n), где А*n есть либо ноль либо единица, а индекс указывает на то, что из всевозможных наборов рассматривается n- ая комбинация. По своему виду конкретные наборы соответствуют n-разрядной записи числа в двоичной системе счисления. Поэтому конкретные наборы часто представляют в виде двоичных или десятичных их числовых эквивалентов. Возможным наборам значений для некоторой логической функции от двух логических переменных А и В соответствуют четыре двоичных числа - 00, 01, 10 и 11 или их десятичных эквиваленты - 0, 1, 2 и 3. Для функции от трех логических переменных соответствуют восемь двоичных чисел - 000, 001, 010 011, 100, 101, 110, 111 или десятичных числа - 0, 1, 2 , 3. 4, 5, 6 и 7. Дли введенных логических функций от F0 до F3, представленных в первой таблице, и от F0 до F15, представленных во второй таблице, их десятичный индекс соответствует десятичному эквиваленту распределения их двоичных значений, если их записать в виде двоичных чисел сверху вниз. Пример 1 Какие из приведенных ниже выражений являются формулами логики высказываний, а какие нет? 1. 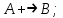 2. 2. 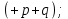 3. 3. 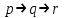 ; 4. ; 4. 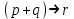 Решение. Здесь выражения под номерами 1, 2 не являются формулами логики высказываний (в 1 - нельзя записать подряд две логические операции, в 2 - высказывание не может начинаться с символа логического сложения). Формулами логики высказываний является формулы под номерами 3 и 4. Иногда вводят в рассмотрение понятие "подформулы". Если F- формула, а - какая-либо ее связная часть, которая сама является формулой, то называется подформулой формулы F. Понятие подформулы не следует путать с понятием связной части формулы. Связная часть формулы - это часть формулы, которая выписана из нее без пропусков. Например, в формуле 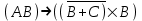 есть следующие подформулы А, В, С, АВ, есть следующие подформулы А, В, С, АВ, 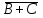 , ,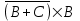 . Никаких других подформул данная формула не имеет. Выражение . Никаких других подформул данная формула не имеет. Выражение 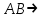 является частью формулы, но подформулой не является. является частью формулы, но подформулой не является. 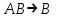 также не является подформулой, поскольку не является се связной частью. Главной подформулой формулы Fназывается такая ее подформула, которая не является частью никакой другой подформулы формулы F. Например, формула также не является подформулой, поскольку не является се связной частью. Главной подформулой формулы Fназывается такая ее подформула, которая не является частью никакой другой подформулы формулы F. Например, формула 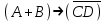 имеет две главные подформулы (А + В) и имеет две главные подформулы (А + В) и 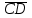 . .Логические формулы допускают различные тождественные преобразования с целью их упрощения или придания им более удобного для применения вида. Запись формулы часто можно упростить: 1) Внешние скобки можно опустить; 2) Если подформула имеет вид 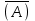 , то скобки можно опустить. Таким образом, правила опускания скобок аналогичны соответствующим правилам опускания скобок в арифметике и алгебре, нужно лишь учитывать приоритетность выполнения логических операции. , то скобки можно опустить. Таким образом, правила опускания скобок аналогичны соответствующим правилам опускания скобок в арифметике и алгебре, нужно лишь учитывать приоритетность выполнения логических операции.Пример 2. Опустить лишние скобки в формуле 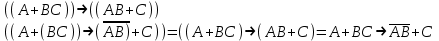 Пример 3. Восстановите опушенные скобки в формуле 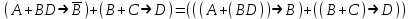 Для каждой формулы алгебры логики может быть построена соответствующая таблица истинности. Задача построения таблицы истинности для формулы, состоящей из n переменных, есть задача построения двоичной функции (Булевой функции), соответствующей данной формуле. Алгоритм построения таблиц истинности Пусть задана логическая формула, и нам надо построить ее таблицу истинности. Для построения таблицы истинности этой формулы необходимо выполнить следующие действия: Определить количество переменных, входящих в формулу и составить таблицу всевозможных значений переменных (наборов, иногда также говорят - оценок переменных), от которых зависит данная формула. Конкретные наборы можно рассматривать как числа в двоичной системе счисления и их удобно располагать в порядке возрастании от 0 до 2n -1, если количество переменных равно n. Провести анализ построения этой формулы с учетом расположения скобок и приоритетности порядка выполнения логических операций. Выписать саму формулу, затем ее главные подформулы, затем под каждой подформулой снова выпишем главные подформулы и т.д. Количество столбцов в таблице должно быть равно сумме количества простых переменных и выделенных подформул плюс один столбец отводится на саму формулу. Общее количество строк должно быть на единицу больше, то есть 2n +1. Одна строка добавляется для записи переменных, всех подформул и самой формулы. Поэтапно сверху вниз строить таблицу истинности, двигаясь слева направо, для всех подформул (лучше по порядку их выполнения). В результате получим таблицу истинности для исходной формулы. Пример Построить таблицу истинности для логической функции 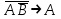 . .
Отношения между формулами алгебры логики Из полученной выше таблицы истинности видно, что истинностные значения формулы 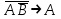 точно совпадают со значением логической переменной А. Они либо одновременно ложны, либо одновременно истинны. Такие формулы называются равносильными или эквивалентными. Равносильные формулы могут содержать различное количество логических переменных. Даже в рассмотренном примере, левая часть зависит от двух логических переменных - А и В, а правая часть только от одной логической переменной А. Важно, чтобы формулы, которые называются равносильными, имели одинаковые значения при одинаковых наборах логических переменных по тем переменным, от которых они зависят. Для обозначения равносильности пользуются обычно знаком равенства: точно совпадают со значением логической переменной А. Они либо одновременно ложны, либо одновременно истинны. Такие формулы называются равносильными или эквивалентными. Равносильные формулы могут содержать различное количество логических переменных. Даже в рассмотренном примере, левая часть зависит от двух логических переменных - А и В, а правая часть только от одной логической переменной А. Важно, чтобы формулы, которые называются равносильными, имели одинаковые значения при одинаковых наборах логических переменных по тем переменным, от которых они зависят. Для обозначения равносильности пользуются обычно знаком равенства: 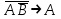 =А =АУпрощение логических формул может также проводиться но правилу подстановки. Если в формуле есть какая-либо подформула, которая равносильна другой формуле, то эту подформулу можно заменить равносильной. Для такой подстановки используются таблицы истинности, а на практике наиболее часто применяются законы математической логики. С помощью таблиц истинности для формул, имеющих небольшое количество переменных и число логических операций, можно достаточно просто проверить равносильность формул. Пример Проверить равносильность формул с помощью таблиц истинности: 1. 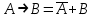 2. 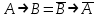 3. 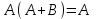 4. 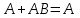 5. 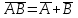 6. 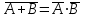
Таким образом, равносильными являются формулы 1 и 2, 3 и 4. Равносильные формулы можно рассматривать как "имена"' одного и того же объекта, то есть они взаимозаменяемы. В математике это достаточно привычная ситуация, когда некоторое математическое выражение заменяется любым ему тождественным. В простейших случаях некоторое число можно заменить другим тождественным представлением. Например, дробь 1/2 можно заменить на 3/6, а единицу заменить на сумму квадратов синуса и косинуса некоторого угла. Таким образом, замена одной формулы на равносильную ей, ничего не меняет. Кроме понятия равносильности формул, для определения отношения между различными формулами пользуются также такими понятиями как совместимость, несовместимости противоположность, логическое следование. Две формулы называются совместимыми, если хотя бы при одной оценке miпеременных (наборе переменных), они одновременно являются истинными. В противном случае они несовместимые. Две формулы называются противоположными (инверсными), если при любой оценке переменных miони принимают противоположные значения и в этом случае каждая из формул является отрицанием (инверсией) другой. Формула В называется логическим следствием формулы А, если при любых оценках переменных, входящих в формулы, импликация А  В принимает только одно значение - истина. В принимает только одно значение - истина.Всю совокупность формул логики высказываний можно разделить на три класса: Нейтральные или выполнимые формулы. Формулы принимают как значение 1 (истинна), так и 0 (ложно). Тождественно-истинные формулы (тавтологии). Формулы принимают только значение 1 (истинно) независимо от логических значений входящих в них переменных. Тождественно-ложные формулы (противоречия или контрадикции). Формулы принимают только значение 0 (ложно) независимо от логических значений входящих в них переменных. Замечание. Такая же классификация справедлива и для логических функций. Все введенные определения для логических формул справедливы для логических функций и наоборот. Тождественно-истинные и тождественно-ложные формулы называют также невыполнимыми. Тождественно-истинные и тождественно-ложные формулы играют большую роль в математической логике. Эго связано с тем, что при любых наборах значений логических переменных они сохраняют постоянное значение истинности и, к тому же, являются взаимоинверсными. С помощью тождественно-истинных формул, как правило, записываются основные законы математической логики. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||