Курс лекций схемотенхника. Курс лекций схемотехника. Курс лекций по дисциплине Цифровая схемотехника для специальности

• Название: Курс лекций по дисциплине Цифровая схемотехника для специальности
• Анкор: Курс лекций схемотенхника
• Дата: 08.02.2023
• Размер: 0.83 Mb.
• Имя файла: Курс лекций схемотехника.docx
• Тип: Курс лекций; #926629
• страница: 5 из 14

Примеры

Пример 2.1.1.

Найти сумму чисел 1010₂и 10101 ₂

Решение.

01010

+ 10101

11111

Учитывая, что 1010₂= 10₁₀и 10101₂ = 21₁₀получаем 10 + 21 =31

Действительно, согласно формуле



Пример 2.1.2.

Найти разность чисел 10101₂и 1010₂

10101

-01010

01011

Пример 2.1.3. Найти произведение чисел 10111₂ и 11₂

Решение.

10111

* 11

+10111

10111

1000101

Пример 2.1.4. Найти частное чисел 110101110₂и 1010₂.
Решение.

В частном смело пишем первую 1, т.к. число в двоичной системе не может начинаться с 0. Умножаем эту 1 на делитель, результат правильно записываем под делимом, соблюдая разрядность. Выполняем вычитание по правилам вычитания в двоичной системе счисления. Сносим следующую цифру делимого, и полученное число сравниваем с делителем. В данном случае – полученное число меньше делителя, в частном записываем 0 (в противном случае – 1). Сносим следующую цифру делимого. Получили число равное делителю, в частном записываем 1, и т.д

110101110|1010

-1010 101011

1101

• 
  1010
  

1111

• 
  1010
  

1010

• 
  1010
  

0

Пример 2.1.5. Провести сложение в восьмеричной системе счисления
числа 5 с числами 1, 2, 3, 4.

Решение. 5+1 = 6,

5 + 2=7,

5 + 3 = 10,

5 + 4 = 11

Пример 2.1.6. Выписать таблицу умножения для числа 6 с числами от 1 до 11 в восьмеричной системе счисления.

Решение.



Пример 2.1.7. Найти сумму в восьмеричной системе счисления чисел 365,5 и 74,3.

Решение.

365,5

+ 47,3

462,0

Пример 2.1.8. Найти сумму в шестнадцатеричной системе счисления чисел А6Е,9 и FD,8
Решение.

А6Е,9

+ FD,8
B6C,1

Пример 2.1.9.

Найти разность в восьмеричной системе счисления от чисел 140 и 32.

Решение.

10₈8₁₀ 8-2=6

14 0

- 3 2

10 6

Пример 2.1.10. Найти разность в восьмеричной системе счисления чи­сел 365,5 и 74,3.

Решение.

16-7

365,5

- 74,3

271,2

Пример 2.1.11.

Найти разность в шестнадцатеричной системе счисле­ния чисел A6E,9 иFD,8.

Решение.

16-F=7

A6E,9

- FD,8

971,1

Пример 2.1.12. Заданы числа А₁₆= FA, B₁₆ = 75. Найти А + В и А-В.

Решение.

FA FA

+ 75 - 75

16F 85

Пример 2.1.13. Найти произведение в троичной системе счисления чи­сел 122 и 21.

Х10	Х3
0	0
1	1
2	2
3	10
4	11

Решение.

122

* 21

122

+1021

11102

Пример 2.1.14. Найти произведение в восьмеричной системе счисления
чисел 706 и 52.

Решение.

706

* 52

1614

+ 4336

45174

Пример 2.1.15.

Найти произведение в шестнадцатеричной системе счисления чисел 122 и 21.

122

*21

122

+244

2562

Пример 2.1.16. Найти А+В, А-В, 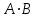и А/В, если А=144₆, В=24₆

Решение

Х10	Х6
0	0
1	1
2	2
3	3
4	4
5	5
6	10
7	11
8	12
9	13
10	14
11	15
12	20
13	21
14	22
15	23
16	24

144 + 24 212

144 - 24 120

144 *24 1104 +332 4424

144|24 144 4 0

Пример 2.1.17.

Найти произведение в шестнадцатеричной системе счисления чисел 706 и 52.

Решение.

706

*52

Е0С

+231Е

23FEC
Таблица 2.1.2

Эквиваленты в системах счисления				Эквиваленты в системах счисления
10 СС	2 СС	8 СС	16 СС	10СС	2СС	8 СС	16 СС
0	0	0	0	11	1011	13	В
1	1	1	1	12	1100	14	С
2	10	2	2	13	1101	15	D
3	11	3	3	14	1110	16	Е
4	100	4	4	15	1111	17	F
5	101	5	5	16	10000	20	10
6	110	6	6	17	10001	21	11
7	111	7	7	18	10010	22	12
8	1000	10	8	19	10011	23	13
9	1001	11	9	20	10100	24	14
10	1010	12	А	21	10101	25	15

Числовые эквиваленты в различных системах счисления
10 СС	2СС	4СС		8СС		16 СС
10 СС	2СС	4 СС	2СС (диада)	8 СС	2СС (триада)	16 СС	2СС (тетрада)	4СС (диада)
0	0	0	00	0	000	0	0000	00
1	1	1	01	1	001	1	0001	01
2	10	2	10	2	010	2	0010	02
3	11	3	11	3	011	3	0011	03
4	100	10	0100	4	100	4	0100	10
5	101	11	0101	5	101	5	0101	11
7	111	13	0111	7	111	7	0111	13
6	110	12	0110	6	110	6	0110	12
8	1000	20	10 00	10	001 000	8	1000	20
9	1001	21	10 01	11	001 001	9	1001	21
10	1010	22	10 10	12	001 010	А	1010	22
11	1011	23	10 11	13	001 011	B	1011	23
12	1100	30	1100	14	001 100	С	1100	30
13	1101	31	11 01	15	001 101	D	1101	31
14	1110	32	11 10	16	001 010	Е	1110	32
15	1111	33	1111	17	001 011	F	1111	33
16	10000	100	100 00	20	001 100	10	0001 0000	01 00

Таблица сложения в восьмеричной системе счисления



Тема 1.3 Кодирование и обработка чисел

1. 
   Прямой, обратный и дополнительные коды чисел
   

Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (нуль или единица) перед его старшим числовым разрядом.

Пример_3_.'>Пример__2.'>Пример 1.

A10=+10 A2=+1010 [A2]П=0:1010;

B10= -15 B2= -1111 [B2]П=1:1111.

Точечной вертикальной линией здесь отмечена условная граница, отделяющая знаковый разряд от значащих.
Обратный код двоичного числа образуется по следующему правилу. Обратный код положительных чисел совпадает с их прямым кодом. Обратный код отрицательного числа содержит единицу в знаковом разряде числа, а значащие разряды числа заменяются на инверсные, т.е. нули заменяются единицами, а единицы - нулями.

Пример 2.

A10=+5 A2=+101 [A2]П=[A2]OK=0:101;

B10= -13 B2= - 1101 [B2]OK=1:0010.

Свое название обратный код чисел получил потому, что коды цифр отрицательного числа заменены на инверсные. Укажем наиболее важные свойства обратного кода чисел:

• 
  сложение положительного числа С с его отрицательным значением в обратном коде дает так называемую машинную единицу МЕок= 1: 111... 11, состоящую из единиц в знаковом и значащих разрядах числа;
  
• 
  нуль в обратном коде имеет двоякое значение. Он может быть положительным - 0: 00...0 и отрицательным числом - 1; 11... 11. Значение отрицательного нуля совпадает с МЕок. Двойственное представление нуля явилось причиной того, что в современных ЭВМ все числа представляются не обратным, а дополнительным кодом.
  

Дополнительный код положительных чисел совпадает с их прямым кодом. Дополнительный код отрицательного числа представляет собой результат суммирования обратного кода числа с единицей младшего разряда (2° - для целых чисел, 2-k - для дробных).

Пример 3.

A10=+19 A2=+10011 [A2]П=[A2]OK=[A2]ДК=0:10011;

B10=- 13 В2= -1101 [B2]ДК=[B2]OK+20=1:0010 + 1 =1:0011.

Укажем основные свойства дополнительного кода:

• 
  сложение дополнительных кодов положительного числа С с его отрицательным значением дает так называемую машинную единицу дополнительного кода:
  
• 
  МЕ_ДК=МЕ_ОК+2⁰=10: 00…00,
  

т.е. число 10 (два) в знаковых разрядах числа;

• 
  дополнительный код получил такое свое название потому, что представление отрицательных чисел является дополнением прямого кода чисел до машинной единицы МЕдк.
  

Модифицированные обратные и дополнительные коды двоичных чисел отличаются соответственно от обратных и дополнительных кодов удвоением значений знаковых разрядов. Знак “+” в этих кодах кодируется двумя нулевыми знаковыми разрядами, а “-” - двумя единичными разрядами.

Пример 4.

A10=9 A2=+1001 [A2]П=[A2]OK=[A2]ДК=0:1001 [A2]МОК=[A2]МДК=00:1001;

B10= -9 B2= -1001 [B2]OK=1:0110 [B2]ДК=1:0111 [B2]МОК=11:0110 [B2]МДК=11:0111.

Целью введения модифицированных кодов являются фиксация и обнаружение случаев получения неправильного результата, когда значение результата превышает максимально возможный результат в отведенной разрядной сетке машины. В этом случае перенос из значащего разряда может исказить значение младшего знакового разряда. Значение знаковых разрядов “01” свидетельствует о положительном переполнении разрядной сетки, а “10” - об отрицательном переполнении. В настоящее время практически во всех моделях ЭВМ роль удвоенных разрядов для фиксации переполнения разрядной сетки играют переносы, идущие в знаковый и из знакового разряда.