Курс лекций схемотенхника. Курс лекций схемотехника. Курс лекций по дисциплине Цифровая схемотехника для специальности

• Название: Курс лекций по дисциплине Цифровая схемотехника для специальности
• Анкор: Курс лекций схемотенхника
• Дата: 08.02.2023
• Размер: 0.83 Mb.
• Имя файла: Курс лекций схемотехника.docx
• Тип: Курс лекций; #926629
• страница: 3 из 14

Двоичная система счисления (бинарная или диодная система счисления)

Имеет цифровой набор {0,1/}, р=2. В двоичной системе 10₂ = 2₁₀. Иногда вместо индекса 2 для обозначения двоичных чисел используется латинская буква b (binary). Например, 11011b. Смешанное двоичное число можно представить выражением в десятичной системе счисле­ния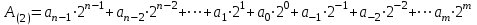



В соответствии с этой формулой целое двоичное число 1000101₍₂₎ можно записать следующим образом:



Смешанное двоичное число 10011,0101₍₂₎ можно записать следующим образом: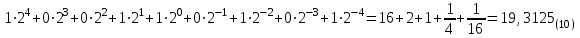

Двоичная система счисления очень широко используется в ЭВМ, поэто­му полезно знать наиболее часто встречающиеся степени числа 2. В таблице 2.1.1 приведены первые 12 степеней числа 2

Таблица 2.1.1

к	1	2	3	4	5	6	7	8	9	10	11	12
2к	2	4	8	16	32	64	128	256	512	1024	2048	4096

Восьмеричная система счисления

Для изображения чисел в восьмеричной системе используются первые 8 цифр десятичной системы счисления - {0,1, 2,3,4,5,6,7}, р = 8. В восьмеричной системе 10₈ = 8₁₀.

В восьмеричной системе счисления, целое число 5375₈ имеет вид:

=2813₍₁₀₎

Шестнадцатеричная система счисления

Для изображения чисел в шестнадцатеричной системе требуется 16 цифр. Первые десять цифр берутся из десятичной системы счисления, а для шести остальных используются шесть заглавных (прописных) букв латинского алфавита - А, В, С, D, Е, F. Заметим, что можно было бы использовать любые другие шесть символов - например, 1,2,3,4,5,6.

Таким образом, в шестнадцатеричной системе имеется на­бор цифр {0, 1. 2, 3, 4, 5, 6, 7, 8, 9, А, В, C, D, Е, F}, р=16. В шестнадцатерич­ной системе 10₁₆ = 16₁₀.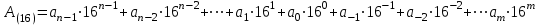



Приведем еще несколько примеров записи целых и дробных шестнадцатеричных чисел.

1АА9,С₍₁₆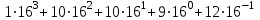₎= = 426,5625

Полезно знать соответствие одинаковых чисел в указанных системах счисления и десятичной системе счисления, которая является наиболее удоб­ной для проведения операций с числами и их восприятия. В таблице 2 1.2 приведены представления десятичных числа от 0 до 21 в двоичной, восьме­ричной и шестнадцатеричной системах счисления.

Таблица 2,1.2

Эквиваленты в системах счисления				Эквиваленты в системах счисления
10 СС	2 СС	8 СС	16 СС	10СС	2СС	8 СС	16 СС
0	0	0	0	11	1011	13	В
1	1	1	1	12	1100	14	С
2	10	2	2	13	1101	15	D
3	11	3	3	14	1110	16	Е
4	100	4	4	15	1111	17	F
5	101	5	5	16	10000	20	10
6	110	6	6	17	10001	21	11
7	111	7	7	18	10010	22	12
8	1000	10	8	19	10011	23	13
9	1001	11	9	20	10100	24	14
10	1010	12	А	21	10101	25	15

2. 
   Преобразование чисел из одной системы в другую
   

Перевод десятичных чисел в другие системы счисления

Перевод целых чисел

Алгоритм перевода (последовательность шагов):

1. 
   Основание новой системы счисления выразить в десятичной с.с. и все последующие действия выполнять в десятичной с.с.
   
2. 
   Последовательно выполнять деление данного числа и получаемых промежуточных частных на основание новой с.с. до тех пор, пока не будет получено частное, меньшее делителя.
   
3. 
   Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
   
4. 
   Составить число в новой системе счисления, записывая его, начиная с последнего частного.
   

Пример 1: Перевести число 37 из десятичной в двоичную систему счисления. (Ответ: 37₁₀ = 100101₂).

37 : 2 = 18 + 1, значит a₀ = 1,

18 : 2 = 9 + 0, значит a₁ = 0,

9 : 2 = 4 + 1, значит a₂ = 1,

4 : 2 = 2 + 0, значит a₃ = 0,

2 : 2 = 1 + 0, значит a₄ = 0,

1 < 2, следовательно, деление следует прекратить, а полученная цифра – это a₅ = 1.

Теперь составим число a₅ a₄ a₃ a₂ a₁ a₀ =100101₂
Пример 2: Перевести число 315 из десятичной в восьмеричную систему счисления. (Ответ: 315₁₀ = 473₈).

315 : 8 = 39 + 3, значит a₀ = 3,

39 : 8 = 4 + 7, значит a₁ = 7,

4 < 7, следовательно, деление следует прекратить, а полученная цифра – это a₂ = 4.

Теперь составим число a₂a₁a₀ = 473₈
Пример 3: Перевести число 315 из десятичной в шестнадцатеричную систему счисления. (Ответ: 315₁₀ = 13B₁₆).

315 : 16 = 19 + 11, значит a₀ = 11,

19 : 16 = 1 + 3, значит a₁ = 3,

1 < 16, следовательно, деление следует прекратить, а полученная цифра – это a₂ = 1.

Теперь составим число a₂a₁a₀ = 13B₁₆

Перевод правильных дробей

Алгоритм перевода:

1. 
   Основание новой системы счисления выразить в десятичной системе счисления и все последующие действия производить в десятичной с.с.
   
2. 
   Последовательно умножать данное число и получаемые дробные части произведений на основание новой системы счисления до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления.
   
3. 
   Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
   
4. 
   Составить дробную часть числа в новой системе счисления, записывая его, начиная с целой части первого произведения.
   

Пример 1: Перевести число 0,1875 из десятичной в двоичную систему счисления. (Ответ: 0,1875 ₁₀ = 0,0011₂).

0	1875 2
a-1 = 0	3750 2
a-2 = 0	7500 2
a-3 = 1	5000 2
a-4 = 1	0000

Теперь составим число 0,a_-1a_-2a_-3 = 0, 0011₂

Пример 2: Перевести число 0,1875 из десятичной в восьмеричную систему счисления. (Ответ: 0,1875 ₁₀ = 0,14₈).

0	1875 8
a-1 = 1	5000 8
a-2 = 4	0000

Теперь составим число 0,a_-1a_-2= 0, 14₈

Пример 3: Перевести число 0,1875 из десятичной в шестнацатеричную систему счисления. (Ответ: 0,1875 ₁₀ = 0,3₁₆).

0	1875 16
+ 1 1	1250 8750
a-1 = 3	0000

Теперь составим число 0,a_-1= 0, 3₁₆

Перевод смешанных чисел

Правило перевода: целая и дробная часть исходного числа переводятся отдельно по рассмотренным выше алгоритмам. В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой (точкой).

Пример: 315,1875₁₀ = 473,14₈ = 13B,3₁₆
Перевод чисел из любой позиционной системы счисления в десятичную

Алгоритм перевода:

1. 
   Расставить значения степеней основания системы счисления для каждой значащей цифры числа.
   
2. 
   Цифры числа в исходной системе счисления привести в соответствие с алфавитом десятичной системы счисления.
   
3. 
   Основание исходной системы счисления выразить в десятичной с.с. и все последующие действия выполнять в десятичной с.с.
   
4. 
   Записать число в развернутой форме и выполнить необходимые арифметические действия.
   

Пример 1: Перевести число 1001,011 из двоичной в десятичную систему счисления. (Ответ: 1001,011 ₂ = 9,375₁₀).

3 2 1 0 -1-2 -3

1001, 01 1 = 123+120+12-2+12-3 = 8+ 1 + 0,25 + 0,125 = 9,37510

Пример 2: Перевести число 726,15 из восьмеричной в десятичную систему счисления. (Ответ: 726,15 ₂ = 470,203125₁₀).

2 1 0 -1-2

726, 15 = 782+281+680+18-1+58-2 = 448+ 16 + 6 + 0,125 + 0,078125 = 470,20312510

Пример 3: Перевести число 10A,F из шестнадцатеричной в десятичную систему счисления. (Ответ: 10A,F ₁₆ = 266,9375₁₀).

2 1 0 -1

10A, A = 1162+10160+1516-1 = 256 + 10 + 0,9375 = 266,937510

Перевод чисел из восьмеричной системы счисления в двоичную и обратно

Чтобы сформулировать правило перевода чисел из восьмеричной системы счисления в двоичную, вспомним рассмотренный ранее кибернетический подход к измерению информации. Уравнение Хартли позволяет определить информационный вес символа iалфавита мощностью N: 2ⁱ =N. Мощность алфавита восьмеричной с.с. равна 8, следовательно, информационный вес каждого символа этого алфавита равен трем битам, т.к. 2³ =8. Известно, что каждый символ двоичного алфавита несет один бит информации, следовательно, для кодирования каждой цифры восьмеричной с.с. требуется 3 цифры двоичной с.с.

Правило перевода: для перевода числа из восьмеричной системы счисления в двоичную необходимо каждую цифру этого числа записать трехразрядным двоичным числом (триадой).

Пример. Записать число 325,27₈ в двоичной системе счисления.

325,278 = 011 010 101, 010 111 8-2 = 11010101,0101112

Для перехода от восьмерично-двоичной системы к двоичной отбрасываются незначащие нули слева для целых чисел и справа - для правильных дробей.

Для перевода числа из двоичной с.с. в восьмеричную необходимо разбить это число вправо и влево от запятой на группы по три разряда – триады и представить каждую группу цифрой в восьмеричной системе счисления. Крайние неполные триады дополняются нулями.

Пример. Записать число 10111011,01101₂ в восьмеричной системе счисления.

10111011,011012 = 010 111 011, 011 010 8-2 = 273,328

Перевод чисел из шестнадцатеричной системы счисления в двоичную и обратно

Правило перевода: Для перевода числа из шестнадцатеричной системы счисления в двоичную необходимо каждую цифру этого числа заменить тетрадой – четырехразрядным двоичным числом.

Пример. Записать число C876,F316 в двоичной системе счисления.

C876,F316 = 1100 1000 0111 0110, 1111 0011 16-2 = 1100100001110110,11110011 2

Правило перевода: Для перевода числа из двоичной системы счисления в шестнадцатеричную необходимо разбить это число вправо и влево от запятой на группы по четыре разряда – тетрады и представить каждую группу цифрой в шестнадцатеричной системе счисления.

Пример. Записать число 1011101101,1011011012 в восьмеричной системе счисления.

1011101101,1011011012 = 0010 1110 1101 , 1011 0110 1000 16-2 = 2ED,B688

3. 
   Арифметические действия в различных системах счисления
   

Действия над числами с основаниями отличными от 10, несколько непривычны, и поэтому вызывают определенные затруднения. Однако правила сложения, вычитания, умножения «столбиком» и деления «уголком», которые используются в деся­тичной системе счисления, применимы в любой системе счисления. Как и в десятичной системе счисления, при сложении чисел единица переноса и стар­ший разряд появляется, если сумма цифр равна или больше основания рсис­темы счисления. При вычитании чисел, если цифра уменьшаемого меньше цифры вычитаемого, то из следующего старшего разряда «занимается» едини­ца основания.

В арифметике все операции, в конечном счете, как будет показано поз­же, могут быть определены через операцию сложения. Рассмотрим ее выпол­нение в системе счисления с основанием р.

Пусть заданы два целых положительных числа в позиционной системе счисления с основанием р. Запишем эти числа в виде: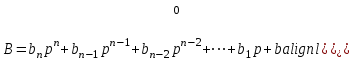





Сумма этих чисел равна числу, которое может быть представлено в ана­логичной форме



Сумма этих чисел вычисляется по следующим правилам:

• 
  операция сложения выполняется поразрядно, начиная с младших разрядов в слагаемых;
  
• 
  в каждом одноименном разряде слагаемых суммируются соответствующие цифры и перенос из предыдущего разряда суммы;
  
• 
  если сумма цифр одноименных разрядов слагаемых и переноса меньше ос­нования системы, то перенос в следующий разряд равен нулю, если сумма цифр равна или больше основания системы - перенос равен единице.
  

Если числа А и Б имеют разное количество разрядов, то для меньшего числа считается, что все цифры недостающих разрядов равны нулю. Количество разрядов суммы S - m может превосходить количество разрядов слагаемых n.

П
a_k b_k
равило сложения в одном разряде можно пояснить рис. 2.1.1, на кото­ром показана схема работы сумматора в k-м разряде.







П_к-1

П_к






S_k



Здесь k означает перенос k -го разряда в (k +1) разряд, который опре­деляется следующими неравенствами:

П_к =0, при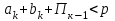

П_к =0, при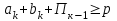

Для суммы, в разряде k, выполняется следующее правило

, где s_k
Цифры суммы чисел могут быть определены только последовательно, на­чиная с младших разрядов. Поэтому в соответствующих суммирующих схемах ЭВМ (многоразрядных сумматорах) операция суммирования должны выпол­няться последовательно, что существенно увеличивает время вычисления.