Курс лекций по дисциплине Инженерная графика раздел Начертательная геометрия

• Название: Курс лекций по дисциплине Инженерная графика раздел Начертательная геометрия
• Анкор: Nachertatelnaya_geometria_Lektsii.doc
• Дата: 27.12.2017
• Размер: 1.98 Mb.
• Имя файла: Nachertatelnaya_geometria_Lektsii.doc
• Тип: Курс лекций; #13135
• страница: 3 из 9

1.4. Метод ортогональных проекций

Сущность метода заключается в том, что заданный геометрический объект ортогонально проецируется на две или три взаимно - перпендикулярные плоскости.

1.5. Ортогональные проекции точки.

Зададим три взаимно - перпендикулярные плоскости (рис. 3) и точку А в пространстве. П₁, П₂, П₃ - плоскости проекций: П₁ - горизонтальная; П₂ -фронтальная; П₃ - профильная. Линии пересечения плоскостей проекций - ОХ, OY, OZ - оси проекций.

Из точки А следует опустить перпендикуляры на три плоскости проекций. Точки пересечения перпендикуляров: с плоскостью П₁ - А₁(горизонтальная проекция точки А); с плоскостью П₂ - А₂(фронтальная проекция); с плоскостью П₃ - А₃(профильная проекция).

Для получения плоского чертежа плоскость П₁повернем вокруг оси ОХ вниз до совмещения с плоскостью П₂, а плоскость П₃совмещаем с плоскостью П₂, поворачивая ее вокруг оси OZ вправо.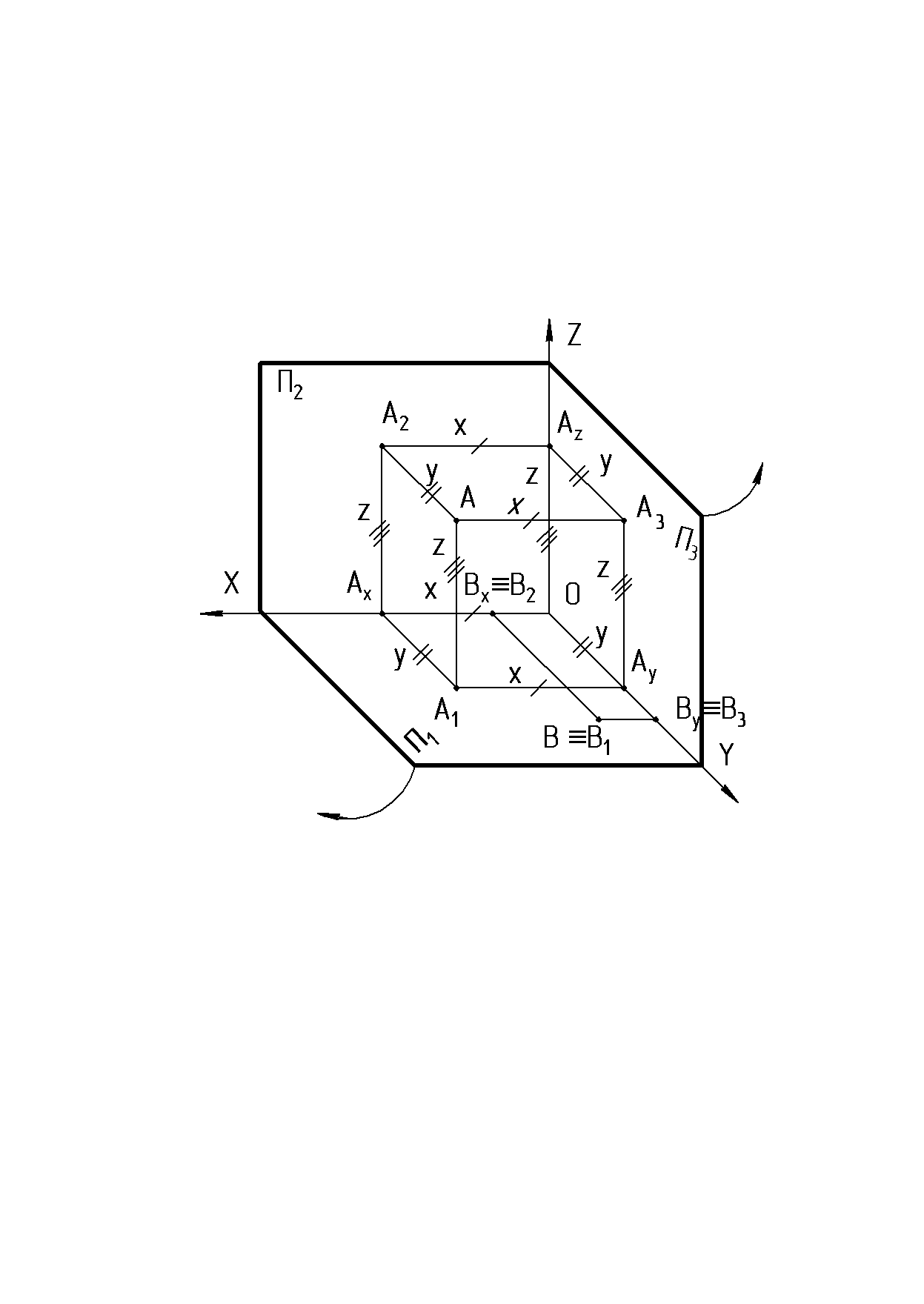



Рис. 3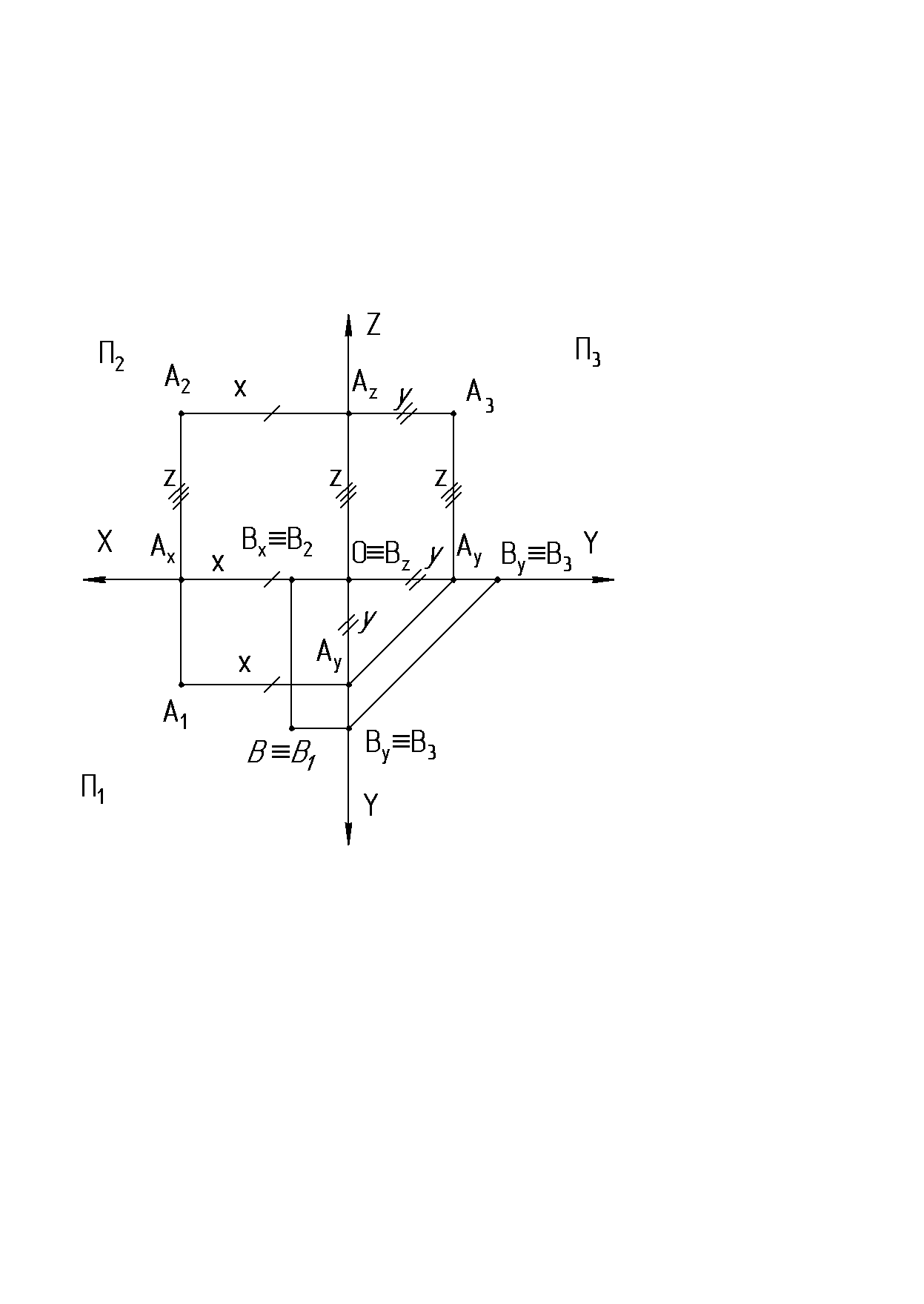



Рис. 4

Плоский чертеж, полученный в результате совмещения плоскостей П₁и П₃ с плоскостью П₂со всем тем, что на этих плоскостях находится, называется комплексным чертежом или «эпюром» Монжа (рис. 4). Эпюр обеспечивает точность и удобность изображений при значительной простоте построений.

Две параллельные проекции точки на взаимно – перпендикулярные плоскости лежат на прямых, перпендикулярных к соответствующей оси проекций и пересекающих эту ось в одной и той же точке. Эти линии принято называть линиями связи. Расстояния от точки до плоскости проекций называются координатами этой точки.

АА₁ = А₂А_х = ОА_z = Z (удаление точки от горизонтальной плоскости проекций)

АА₂ = А₁А_х = А_yО = Y (удаление точки от фронтальной плоскости проекций)

АА₃ = А₁А_y = ОА_x = X (удаление точки от профильной плоскости проекций)

На эпюре две любые точки, лежащие на одной линии связи, определяют ее положение в пространстве, то есть по ним можно определять координаты точек. Третья проекция строится по двум данным. Если точка лежит в плоскости проекций, то на эпюре одна ее проекция совпадает с самой точкой, а другая лежит на оси проекций (В  П₁ рис. 3, 4).

Построить три проекции точки, имеющей координаты 30, 40, 30 (рис.5) (X, Y, Z).

По оси Х откладываем 30, проводим линию связи перпендикулярно оси ХО, на которой параллельно оси Y откладываем 40 - получаем А₁, параллельно оси Z - 30, получаем точку А₂.

Точка А₃строится по двум уже построенным проекциям А₁ и А₂.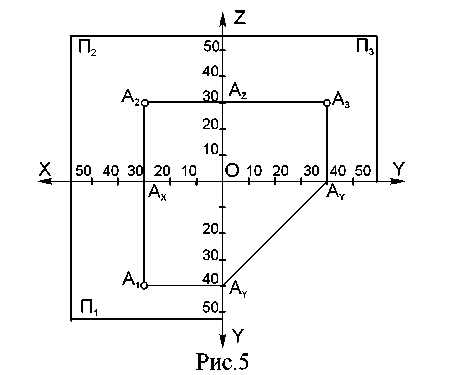



Рис. 5

1.6. Вопросы для самопроверки.

1. 
   В чём заключается операция проецирования точки на плоскость проекций?
   
2. 
   Какие основные виды проецирования геометрических форм на плоскость Вам известны?
   
3. 
   Какие виды параллельных проекций вы знаете?
   
4. 
   Перечислите основные свойства центральных проекций.
   
5. 
   Перечислите основные свойства параллельных проекций
   
6. 
   . Что называют ортогональной проекцией точки?
   
7. 
   Как образуются проекции точки на плоскостях П₁, П₂, П₃?
   
8. 
   В чём заключается метод построения комплексного чертежа?
   
9. 
   Что называют координатами точки пространства в декартовой системе координат, и какие координаты на эпюре определяют ее горизонтальную, фронтальную и профильную проекции?
   
10. 
    Как построить комплексный чертёж точки по её координатам?
    

2. Лекция 2. Ортогональные проекции прямой линии.

2.1. Задание прямой на эпюре.

Прямая линия определяется двумя точками. Поэтому прямая считается заданной, если на эпюре даны проекции двух ее точек..

Проекция прямой в общем случае прямая. Лучи, проецирующие каждую точку прямой, в совокупности составляют проецирующую плоскость, которая пересечет плоскость проекций по прямой линии. Это и будет проекция прямой. Две проекции прямой определяют ее положение в пространстве, так как можно замерить координаты двух точек этой прямой.

Величина проекции отрезка прямой зависит от наклона прямой к плоскости проекций.

А₁В₁ = АВ х cosα

Отсюда, проекция отрезка прямой не может быть больше самого отрезка.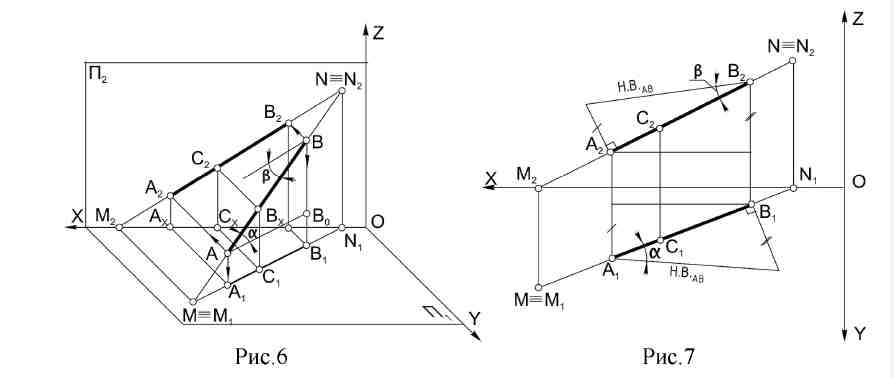

Если α = 0; АВ || пл. П₁; А₁В₁ = АВ

Если α = 90°; АВ пл. П₁; отрезок проецируется в точку.

2.2. Натуральная величина отрезка прямой

По двум проекциям отрезка прямой можно определить его натуральную величину. Для этого достаточно построить прямоугольный треугольник, равный пространственному треугольнику АВ₀В (рис. 6), по двум катетам, величины которых имеются на эпюре (рис. 7).

Натуральная величина отрезка прямой определяется как гипотенуза прямоугольного треугольника, у которого одним катетом служит любая из проекций отрезка, а второй катет равен разности расстояний концов отрезка прямой от той плоскости, на которой взят первый катет. Углом наклона прямой к плоскости проекций считают линейный угол между прямой и ее проекцией на эту плоскость. Для определения угла наклона прямой также надо построить прямоугольный треугольник, у которого гипотенузой является натуральная величина отрезка прямой, а одним из катетов должна быть проекция отрезка на ту плоскость, к которой определяют углы:

 α =АВ ^ П₁ ;  β =АВ ^ П₂.

2.3. Точка на прямой линии

Если точка лежит на прямой, то ее проекции лежат на одноименных проекциях прямой. Проекции точки делят проекции отрезка в таком же отношении, в каком сама точка делит отрезок прямой (рис. 6,7).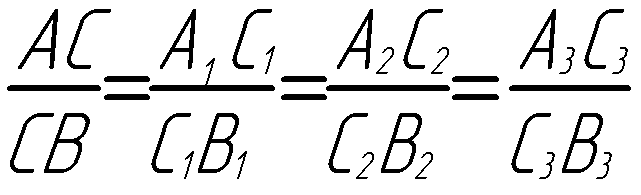



2.4. Следы прямой линии

Точки пересечения прямой с плоскостями проекций называются следами прямой. При трех плоскостях проекций прямая может иметь три следа – горизонтальный, фронтальный и профильный.

Порядок построения следа вытекает из следующих фактов:

1. 
   След прямой – это точка, принадлежащая прямой линии. Значит, проекции следа должны лежать на одноименных проекциях прямой.
   
2. 
   След прямой – это точка, в плоскости проекций. Значит, одна из проекций следа должна лежать на оси. Поэтому, чтобы построить горизонтальный след М (рис. 6, 7) надо продолжить фронтальную проекцию прямой до пересечения с осью, и отметить здесь фронтальную проекцию следа М₂. Горизонтальная проекция следа – М₁и совпадающий с ней след М будут располагаться на горизонтальной проекции прямой и на одной линии связи с фронтальной проекцией. Подобным образом строится фронтальный след (N).
   

2.5. Частные положения прямой

Прямые уровня – это прямые, расположенные параллельно плоскостям проекций (рис. 8, 9).

Проецирующие прямые – прямые, перпендикулярные плоскостям проекций (рис. 10, 11). Каждая из этих прямых имеет отличительные признаки на эпюре.

Например, у прямой, параллельной горизонтальной плоскости проекций, фронтальная проекция параллельна оси проекций. Это происходит потому, что все точки прямой одинаково удалены от плоскости П₁. Если прямую ограничить отрезком, например МN, то на плоскость П₁этот отрезок будет проецироваться в натуральную величину (рис. 8).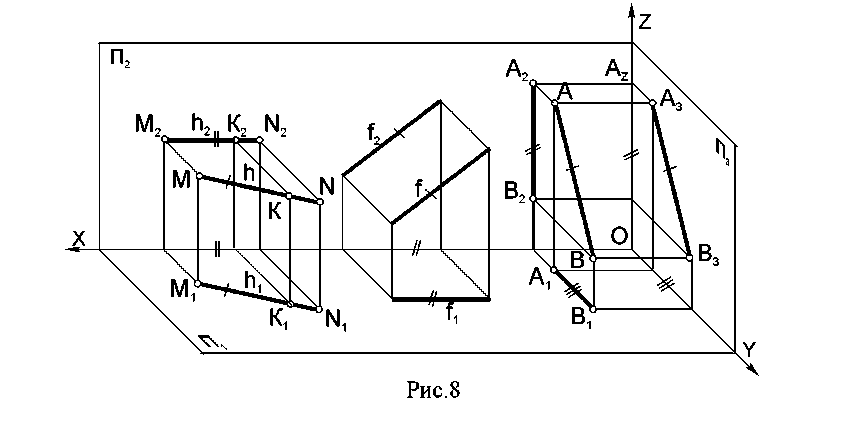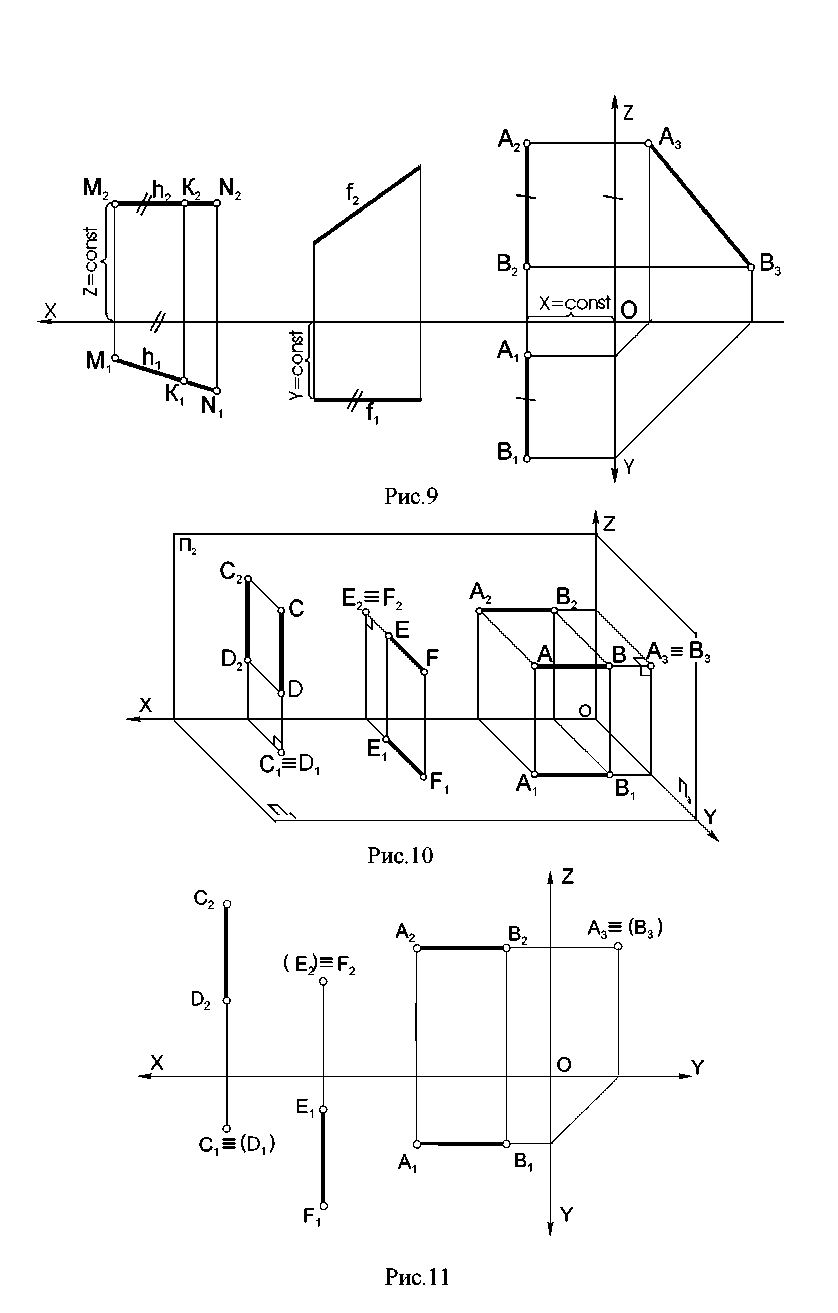






К прямым уровня относятся:

а) горизонталь h - прямая, параллельная плоскости П₁(рис. 8, 9);

б) фронталь f- прямая, параллельная плоскости П₂(рис. 8, 9);

в) профильная прямая (АВ) - прямая, параллельная плоскости П₃(рис. 8, 9);

К проецирующим прямым относятся:

а) горизонтально - проецирующая прямая (CD) - прямая, перпендикулярная плоскости П₁(рис. 10, 11);

б) фронтально - проецирующая прямая (EF) - прямая, перпендикулярная плоскости П₂(рис. 10, 11);

в) профильно - проецирующая прямая (АВ) - прямая, перпендикулярная плоскости П₃(рис. 10, 11).

2.6. Взаимное расположение двух прямых

Две прямые в пространстве могут быть параллельны, пересекаться или скрещиваться. Каждые из этих положений определенным образом отражаются на эпюре (рис. 12).

Если прямые параллельны, то их одноименные проекции параллельны на основании свойств параллельных проекций АВ||СD; А₂В₂ || С₂D₂; А₁В₁ || С₁D₁ (рис.12).

Если прямые пересекаются, то их одноименные проекции пересекаются, и точки пересечения проекций располагаются на одном перпендикуляре к оси, т.е. на одной линии связи

(ЕF∩QL) = К

(E₁F₁∩Q₁L₁) = К₁; (E₂F₂∩Q₂L₂) = К₂

У 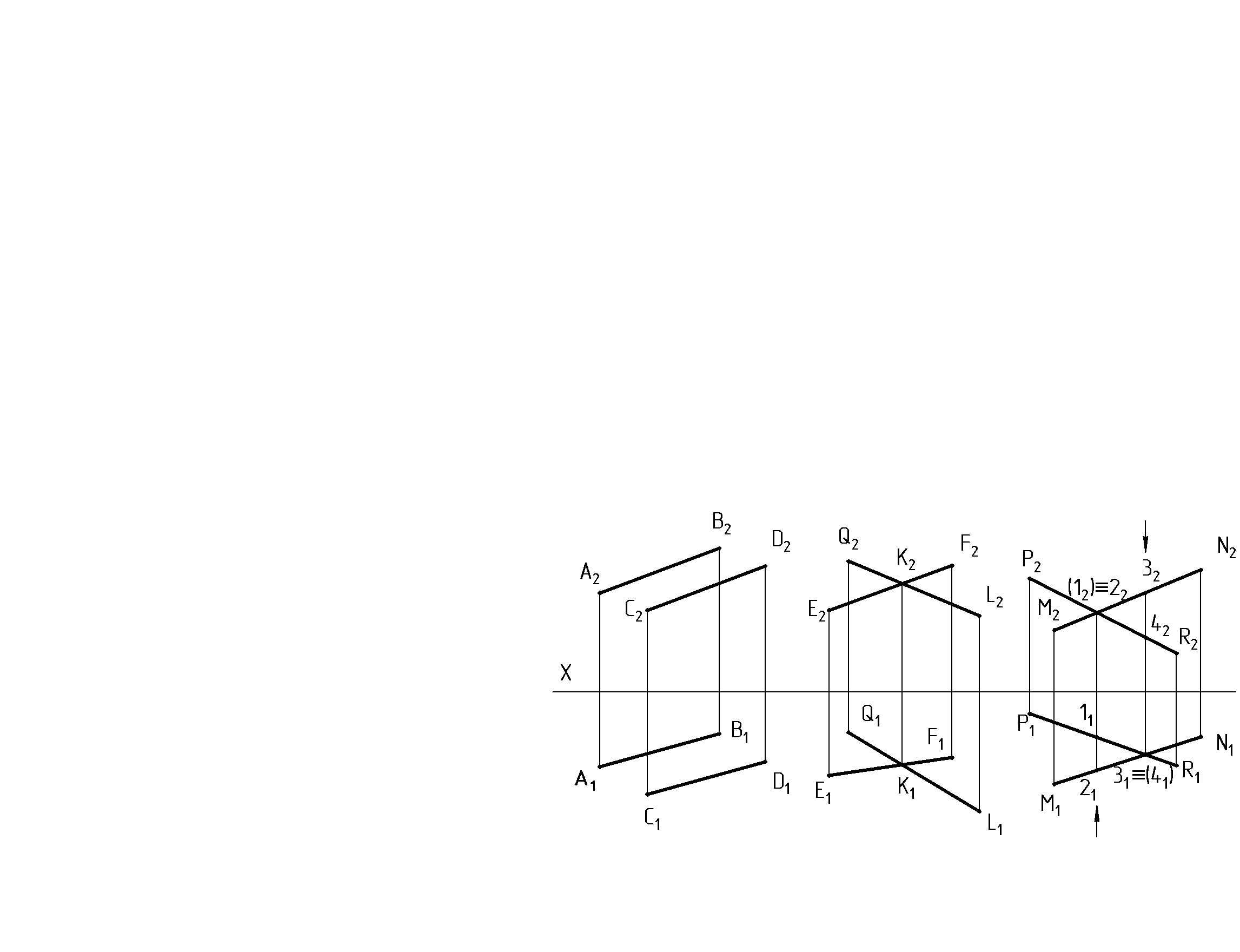скрещивающихся прямых проекции могут пересекаться, но точки пересечения не лежат на одной линии связи МNи РR - скрещивающиеся прямые (рис.12). МN^● РR

Рис.12

По эпюру можно определить видимость точек в случае совпадения их одноименных проекций. Считается, что фронтальная проекция представляет вид спереди, а горизонтальная – вид сверху, и поэтому видимость у каждой проекции своя.

На горизонтальной проекции будет видимой та из конкурирующих точек 3 и 4, которая находится выше - точка 3; на фронтальной – та, которая дальше от фронтальной плоскости, ближе к наблюдателю - точка 2. Невидимые точки на проекциях показывают в скобках (рис.12).

2.7. Угол между пересекающимися прямыми

Угол между пересекающимися прямыми может быть любой – острый, тупой или прямой (рис. 13). Для того, чтобы угол спроецировался на плоскость проекций в натуральную величину, нужно, чтобы обе стороны угла были параллельны этой плоскости проекций (рис. 14).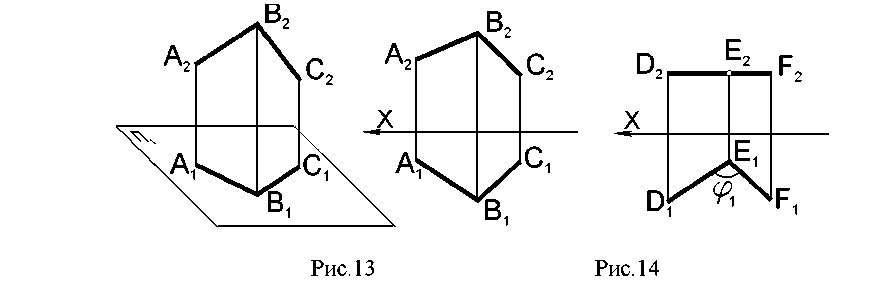



Проецирование прямого угла в истинную величину определяется теоремой «Проецирование прямого угла».

Теорема. Для того, чтобы прямой угол спроецировался на плоскость проекций в натуральную величину, необходимо и достаточно, чтобы одна из его сторон была параллельна этой плоскости, а вторая не перпендикулярна ей. (рис. 15)

Дано:

 АВС=90°; АВ//П₁; ВС неП₁; Доказать:А₁В₁С₁=90°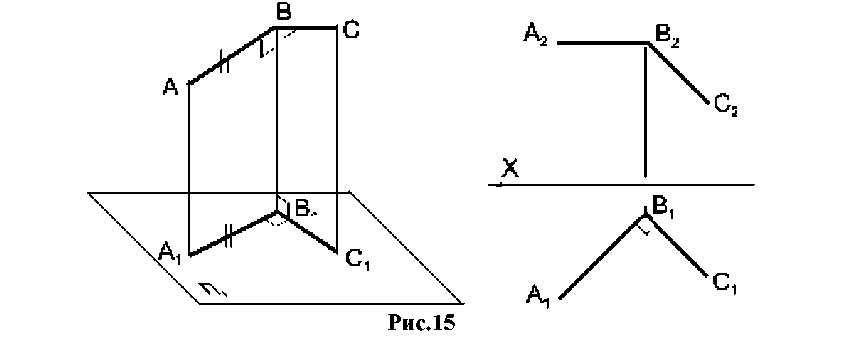



Доказательство. АВ  пл. (ВВ₁СС₁),т.к. АВ  ВС – по условию теоремы, АВ  ВВ₁по условию ортогонального проецирования. АВ || А₁В₁, а если одна из параллельных прямых перпендикулярна плоскости, то вторая также перпендикулярна этой плоскости, а, значит А₁В₁ ВВ₁СС₁. Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, расположенной в этой плоскости, следовательно, А₁В₁ В₁С₁, а, значит,

 А₁В₁С₁ = 90°, что и требовалось доказать.

8. 
   Вопросы для самопроверки.
   

1. 
   Какую прямую называют прямой общего положения?
   
2. 
   Перечислите прямые частного положения, дайте определение каждой из них и укажите особенности их проекций.
   
3. 
   Что называют следом прямой?
   
4. 
   Как построить горизонтальный и фронтальный следы прямой?
   
5. 
   Как задаются на комплексном чертеже параллельные, пересекающиеся и скрещивающиеся прямые?
   
6. 
   Как найти натуральную величину отрезка прямой методом прямоугольного треугольника? Как определить углы наклона отрезка прямой к плоскостям проекций П₁и П₂?
   
7. 
   В каком случае прямой угол проецируется в виде прямого?
   

3. Лекция 3. Ортогональные проекции плоскости.

3.1. Способы задания плоскости в пространстве.

Способы задания плоскости, определяющие однозначно положение плоскости в пространстве (см. рис. 16):

а) три точки, не лежащие на одной прямой;

б) прямая и точка вне прямой;

с) параллельные прямые;

d) пересекающиеся прямые.

е) плоская фигура;

На эпюре плоскость задается проекциями перечисленных геометрических элементов и следами. Эти элементы носят название определителя плоскости (∆).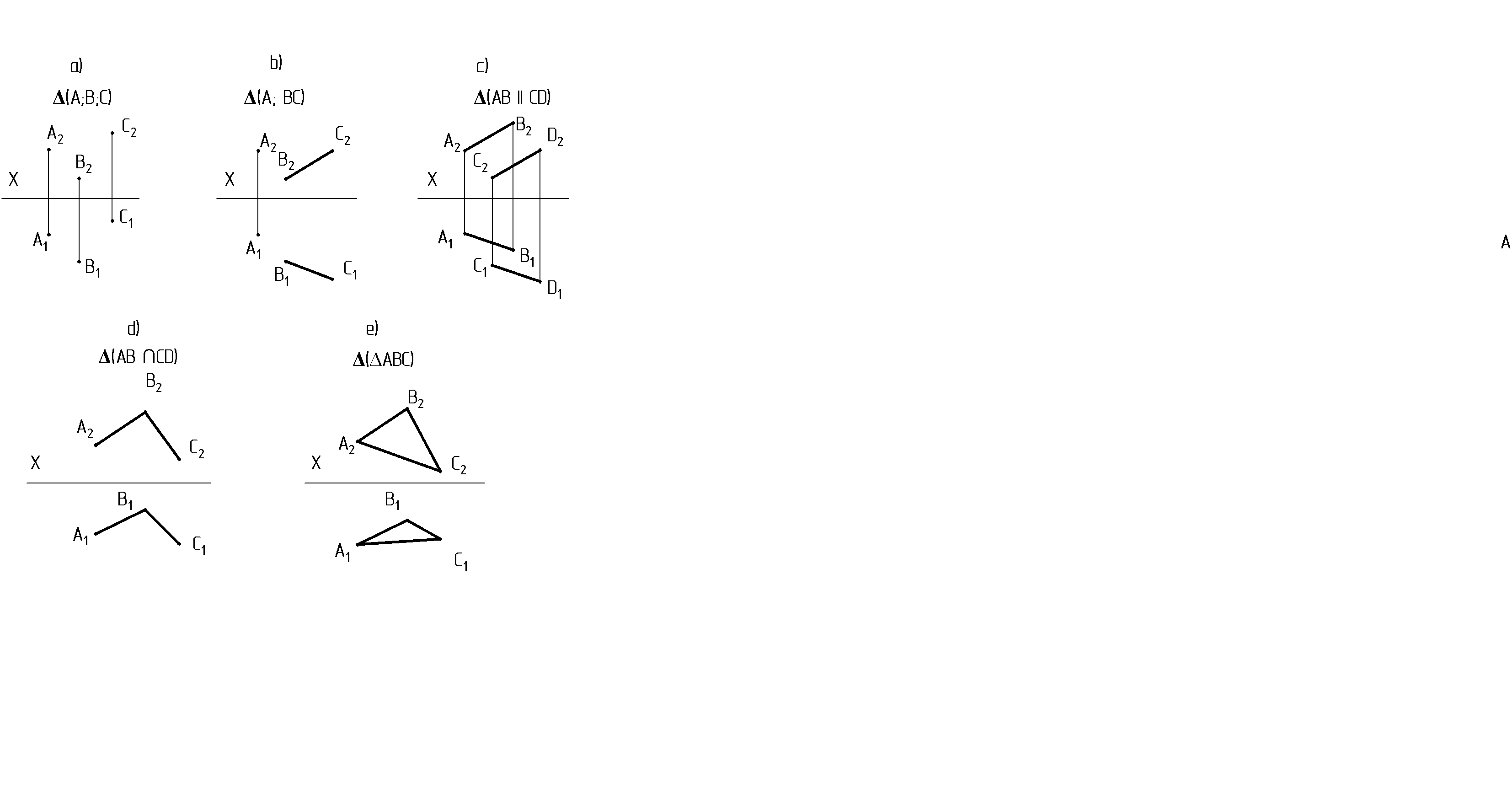



Рис. 16

.



Плоскость в пространстве может быть задана следами (см. рис. 17). Следом плоскости называют линию пересечения данной плоскости с плоскостью проекций. В системе трех плоскостей проекций плоскость общего положения p (не перпендикулярная и не параллельная плоскостям проекций) может иметь три следа – горизонтальный (р₁), фронтальный (р₂), профильный (р₃); Рх, Ру,Рz- точки схода следов (рис. 17)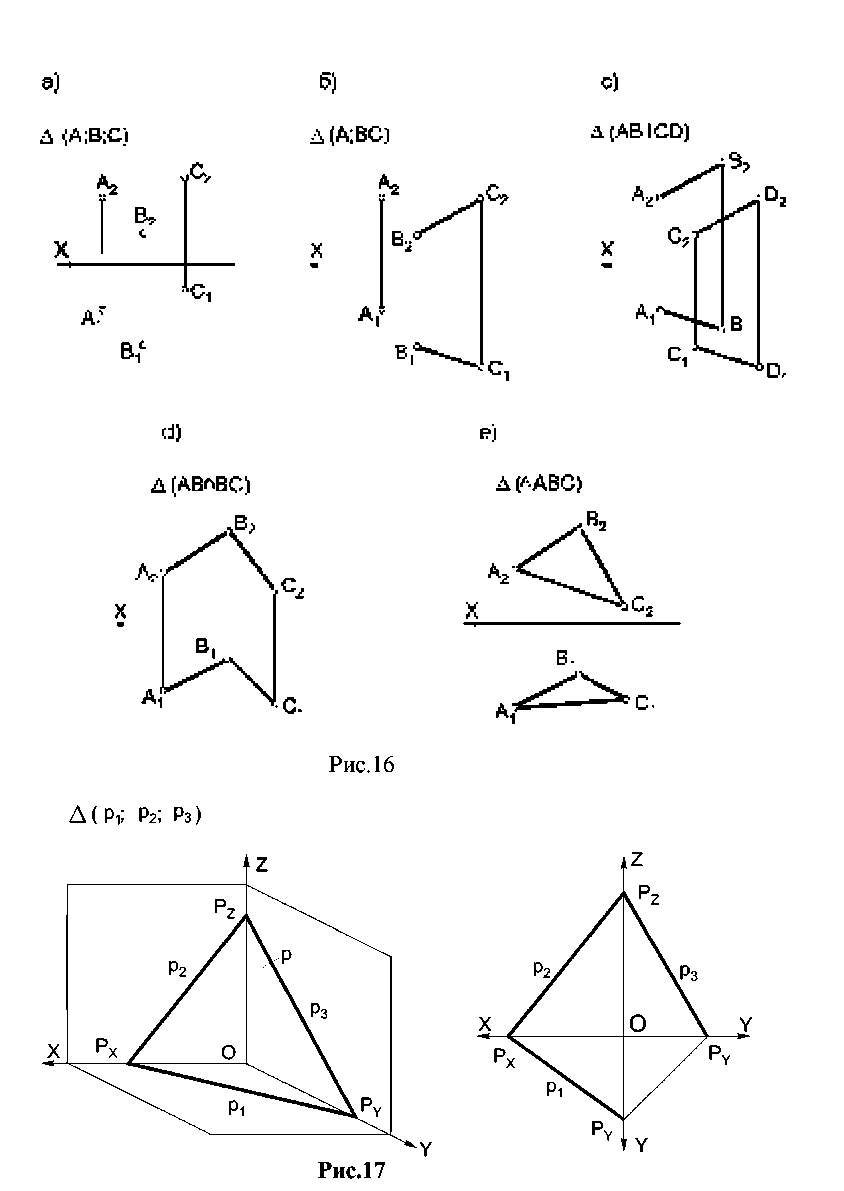



Рис. 17
3.2. Плоскости частного положения.

К плоскостям частного положения относятся:

1. 
   Проецирующие плоскости, т.е. плоскости, перпендикулярные к одной из плоскостей проекций (рис. 18);
   
2. 
   Плоскости уровня – плоскости, параллельные одной из плоскостей проекций (рис. 19).
   

3.3. Проецирующие плоскости

Особенности проецирующих плоскостей:

1. Одна проекция любого элемента, расположенного в проецирующей плоскости, совпадает с соответствующим следом этой плоскости;

2. На эпюре угол наклона заданной плоскости к плоскости проекций проецируется в истинную величину (рис. 18).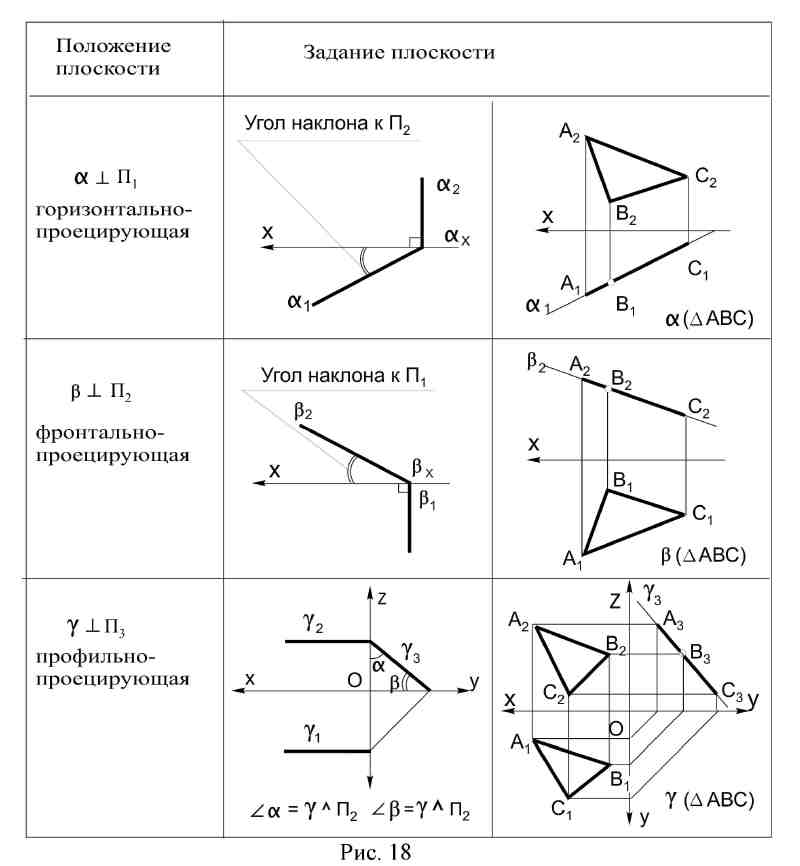


Рис. 18

3.4. Плоскости уровня

Особенностью плоскостей уровня является то, что любая плоская фигура, расположенная в такой плоскости, проецируется на параллельную ей плоскость без искажения, т.е. в истинную величину (рис. 19).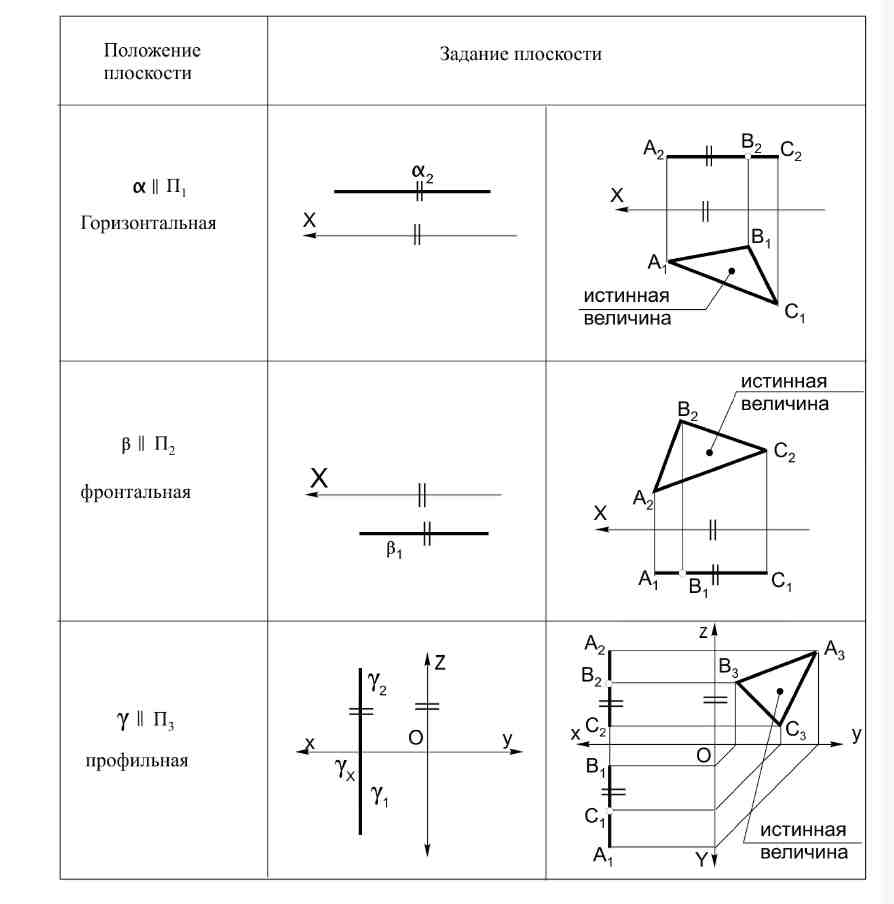



Рис. 19

3.5. Прямая и точка в плоскости.

Для построения элементов, находящихся в плоскости общего положения, нужно руководствоваться двумя правилами:

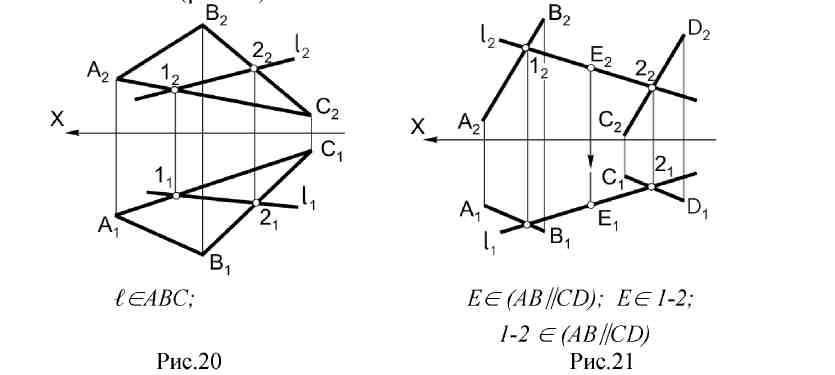1. 
   Прямая линия принадлежит плоскости, если она проходит через две точки, лежащие в плоскости или если она проходит через точку, лежащую в плоскости и параллельно другой прямой, расположенной в этой плоскости (рис. 20);
   

1. 
   Точка лежит в плоскости, если она лежит на прямой, расположенной в этой плоскости (рис. 21).