Курс лекций по дисциплине Инженерная графика раздел Начертательная геометрия

• Название: Курс лекций по дисциплине Инженерная графика раздел Начертательная геометрия
• Анкор: Nachertatelnaya_geometria_Lektsii.doc
• Дата: 27.12.2017
• Размер: 1.98 Mb.
• Имя файла: Nachertatelnaya_geometria_Lektsii.doc
• Тип: Курс лекций; #13135
• страница: 4 из 9

3.6. Главные линии плоскости.

Горизонталь (h) - прямая лежащая в плоскости и одновременно расположенная параллельно плоскости П₁ (рис 22). Фронталь (f) - прямая лежащая в плоскости и параллельная плоскости П₂.Линия наибольшего наклона - это прямая лежащая в плоскости и перпендикулярная или горизонталям или фронталям плоскости. С помощью линии наибольшего наклона определяется угол наклона плоскости к плоскостям проекций. Линия наибольшего наклона расположенная перпендикулярно горизонталям плоскости называется еще линией ската плоскости (ВК рис 22).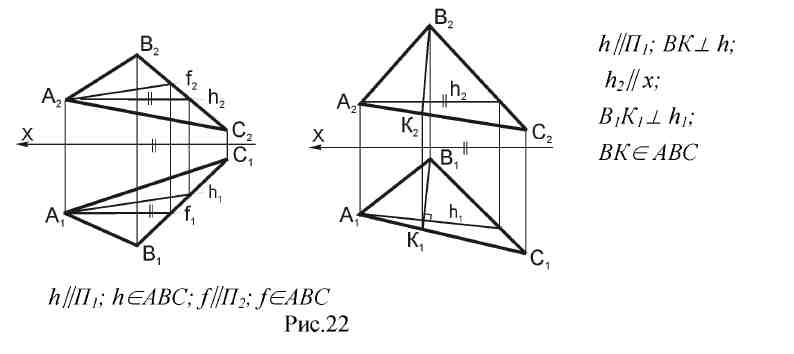



С помощью линии ската определяется угол наклона плоскости АВС к горизонтальной плоскости проекций. Для этого необходимо способом прямоугольного треугольника определить ее натуральную величину и угол между натуральной величиной и горизонтальной проекцией будет искомый угол.

3.7. Вопросы для самопроверки.

1. 
   Перечислите и изобразите графические способы задания плоскости на комплексном чертеже.
   
2. 
   Что понимают под следом плоскости?
   
3. 
   Какую плоскость называют проецирующей и каковы ее графические признаки на чертеже?
   
4. 
   Дайте графические характеристики плоскостям: горизонтально - проецирующей, фронтально – проецирующей, профильно – проецирующей.
   
5. 
   Какую плоскость называют плоскостью уровня?
   
6. 
   Какую плоскость называют горизонтальной? Фронтальной? Профильной? Изобразите их на чертеже.
   
7. 
   Назовите признаки принадлежности прямой плоскости, точки плоскости.
   
8. 
   Покажите на чертеже, как можно прямую заключить в плоскость.
   
9. 
   Назовите главные линии плоскости.
   
10. 
    Как определить угол наклона плоскости к горизонтальной плоскости проекций?
    

4. Лекция 4. Взаимное расположение прямой и плоскости, и двух плоскостей.

4.1. Прямая, параллельная плоскости.

Прямая, параллельная плоскости, если она параллельна какой – либо прямой, принадлежащей плоскости (рис.23).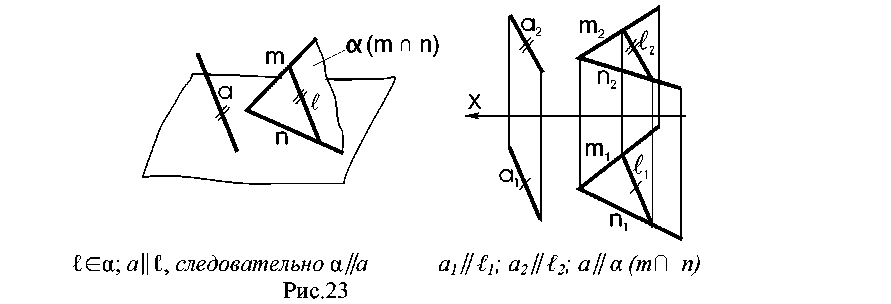



4.2. Параллельные плоскости.

Две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости (рис.24).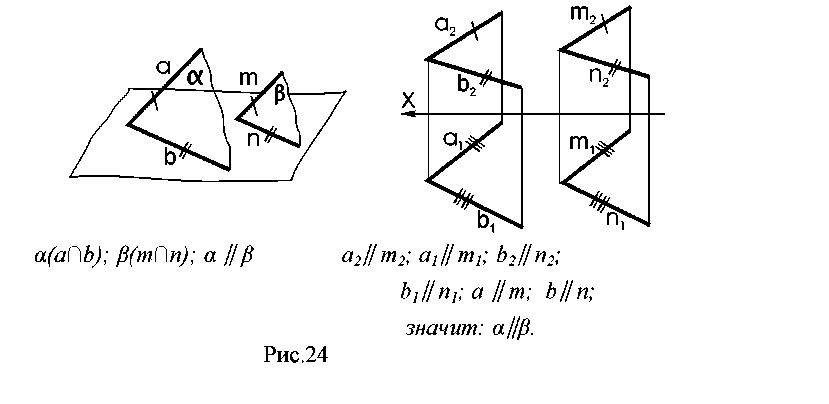


4.3. Прямая, перпендикулярная плоскости.

Прямая, перпендикулярна плоскости, если она перпендикулярна к двум пересекающимся прямым данной плоскости. Из этого следует, что перпендикуляр к плоскости перпендикулярен ко всякой прямой, лежащей в этой плоскости, в том числе к горизонтали и фронтали плоскости. Ранее было доказано, что прямой угол проецируется на плоскость проекций как прямой, если хотя бы одна из его сторон параллельна плоскости проекций. Следовательно, горизонтальная проекция перпендикуляра (на эпюре) перпендикулярна горизонтальной проекции горизонтали плоскости; аналогично – фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали (рис. 25). Это является графическим признаком перпендикулярности прямой и плоскости.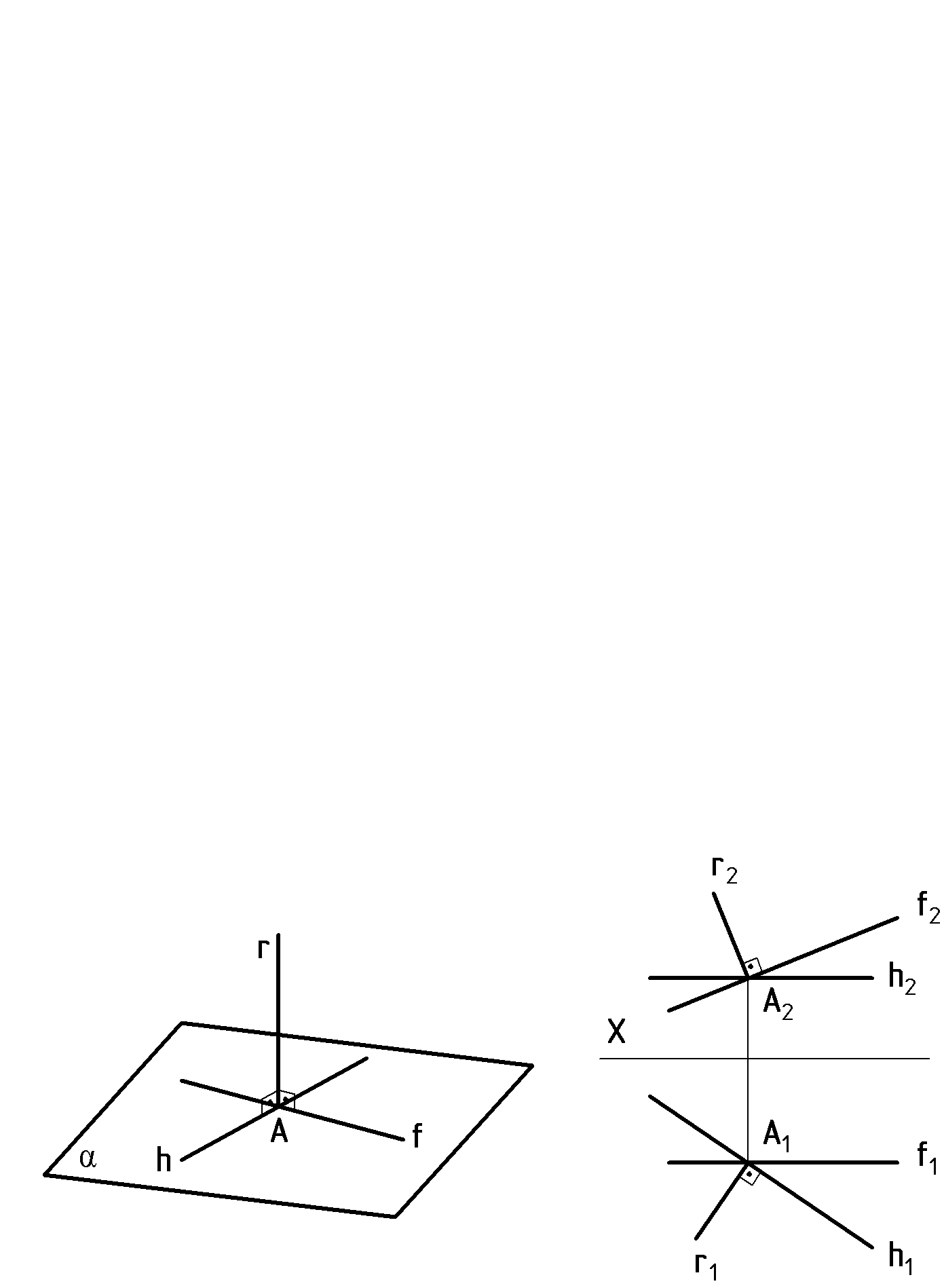



Рис. 25

Пример: Через точку А провести прямую, перпендикулярную плоскости ВСD.

В плоскости проводят горизонталь (h) и фронталь (f) и затем, используя графический признак перпендикулярности прямой и плоскости, проводят

А₁К₁ h₁ ; А₂К₂f₂(рис.26).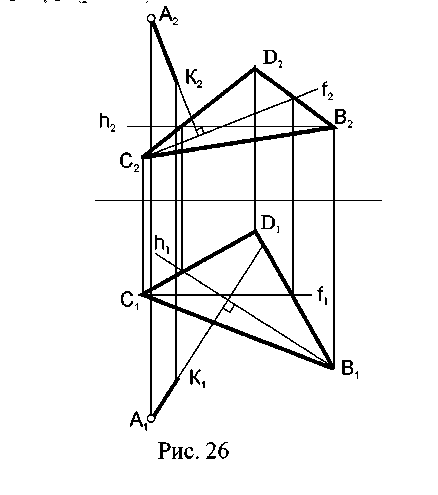


4.4. Взаимно - перпендикулярные плоскости.

Построение взаимно - перпендикулярных плоскостей основано на одном из следующих положений:

1. 
   Если прямая перпендикулярна к какой - либо плоскости, то всякая плоскость, проведенная через эту прямую, будет перпендикулярна первой плоскости.
   
2. 
   Если плоскость перпендикулярна к какой - либо прямой другой плоскости, эти плоскости взаимно перпендикулярны (рис.27).
   

α  β; КL α ; КL β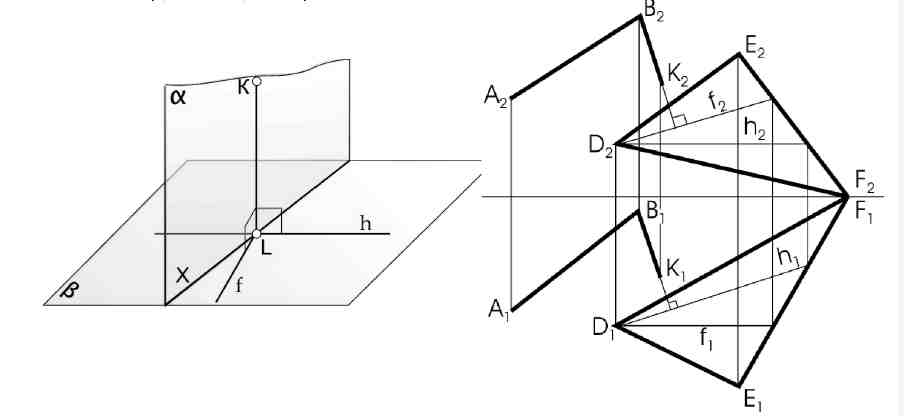



Рис.27 Рис.28

Чтобы на эпюре построить плоскость (α), перпендикулярную данной (β), необходимо, чтобы одна из них проходила через перпендикуляр к другой.

Пример:

Через прямую АВ провести плоскость (α), перпендикулярную заданной β (DЕF) (рис.28).

Искомую плоскость задаем пересекающимися прямыми, одна из которых АВ, другая - перпендикуляр к плоскости DЕF. Для этого в плоскости проводим горизонталь (h) и фронталь (f), а затем проводим В₂К₂f₂; В₁K₁h₁,; ВКDЕF; (АВ∩ВК) DЕF.

4.5. Пересечение плоскостей.

Построение линии пересечения плоскостей - одна из основных задач начертательной геометрии. Она относится к так называемым позиционным задачам. К ним относятся задачи на принадлежность геометрических элементов и на пересечение геометрических объектов, например, пересечение прямой или плоскости с поверхностью, пересечение двух поверхностей и, в частности, задача на пересечение двух плоскостей. Две плоскости пересекаются по прямой линии, поэтому для определения линии пересечения плоскостей необходимо определить две точки этой прямой. Для определения двух общих точек линии пересечения проводят две вспомогательные плоскости - посредники частного положения. Каждая вспомогательная плоскость определяет точку, которая одновременно принадлежит двум данным плоскостям (точка К). Рекомендуется вспомогательные плоскости использовать проецирующими, или уровня (рис. 29).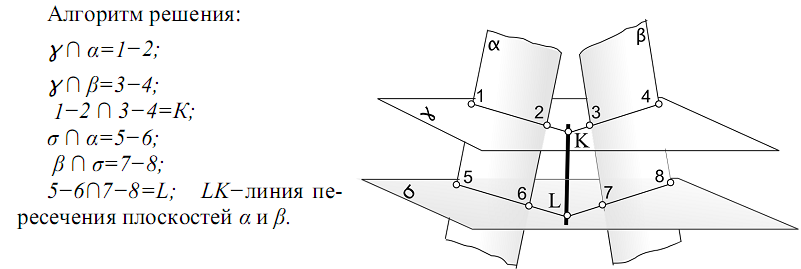



Рис.29

Пример: Построить линию пересечения плоскостей αи β

α (АВ∩ВС); β (DE║FM)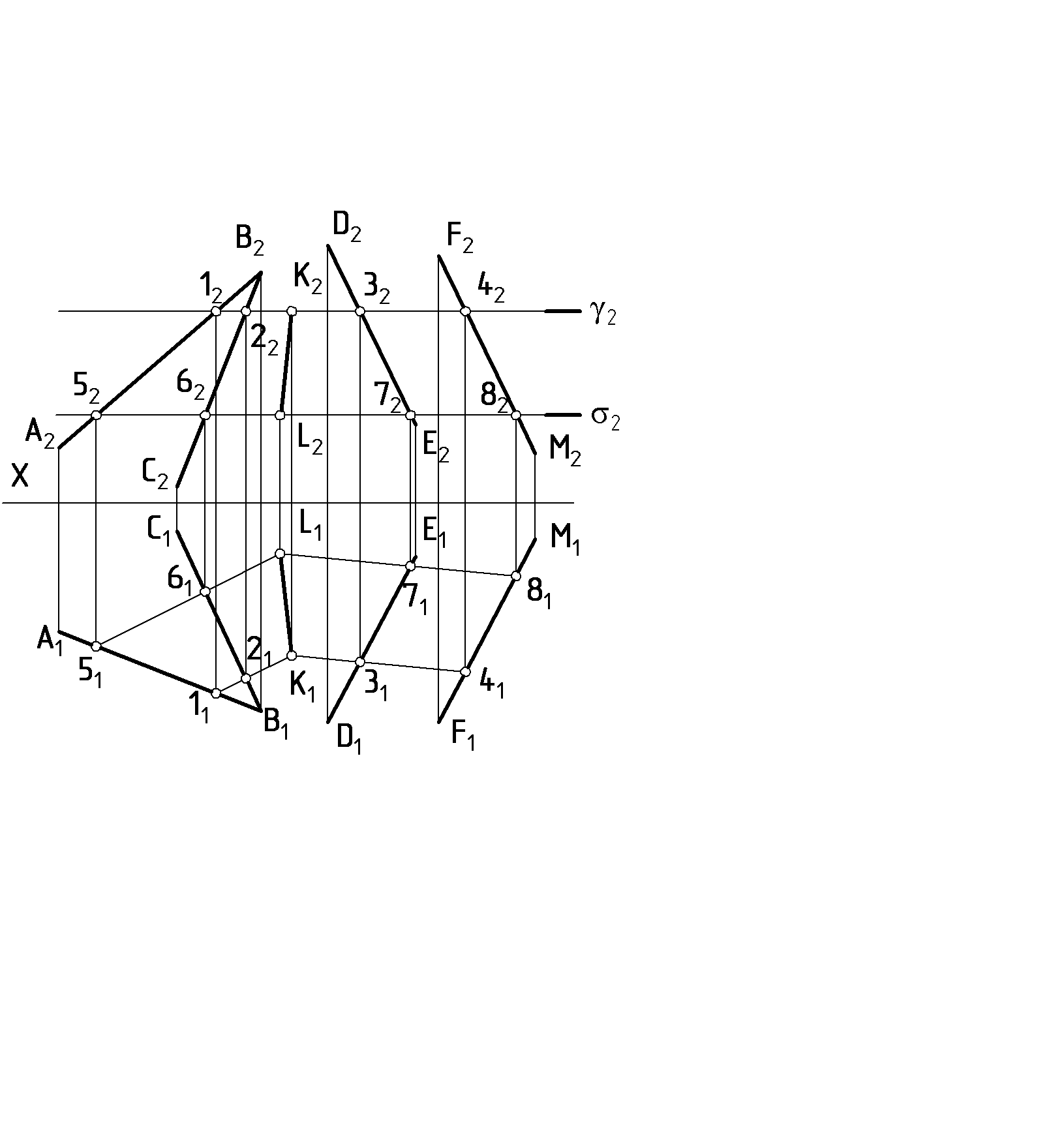



Рис. 30

Алгоритм решения:

γ ∩ α = 1-2; γ ∩ β = 3-4; 1-2 ∩ 3-4 = К;

σ ∩ α = 5-6; σ ∩ β = 7-8; 5-6 ∩ 7-8 = L;

KL = α ∩ β.

Рассмотрим частный случай пересечения плоскостей, когда одна из них проецирующая (рис.31).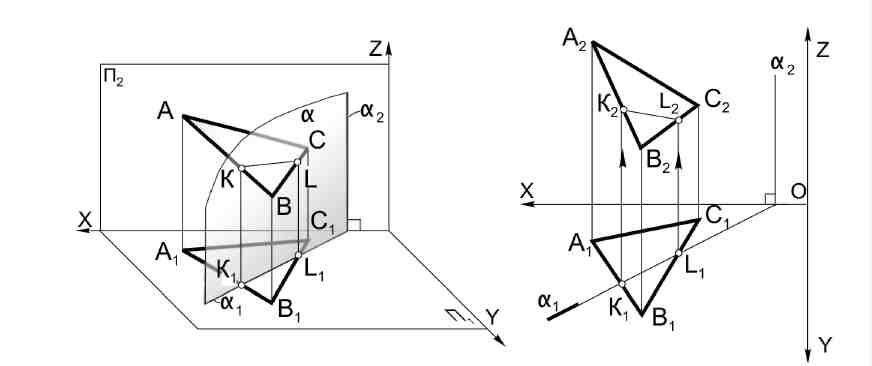



Рис.31

Если одна из пересекающихся плоскостей - проецирующая, то одна из проекций ее линии пересечения совпадает с ее проецирующим следом. Горизонтальная проекция К₁L₁линии пересечения лежит на горизонтальном следе α₁горизонтально - проецирующей плоскости α. Фронтальная проекция линии пересечения К₂L₂определяется линиями связи.

4.6. Пересечение прямой с плоскостью.

Задача на пересечение прямой линии с плоскостью является также одной из основных задач начертательной геометрии. Она входит составной частью в решения различных задач по всем разделам курса.

Пример: Определить точку пересечения прямой ЕFс плоскостью β (рис.32).

Порядок решения задачи (алгоритм решения):

1. 
   Провести через данную прямую вспомогательную плоскость (удобнее проецирующую);
   
2. 
   Построить линию пересечения данной и вспомогательной плоскостей 1-2= β ∩ α ;
   
3. 
   Отметить искомую точку на пересечении данной прямой с линией пересечения плоскостей. К=(1-2)∩ ЕF К=ЕF∩ β (рис.32а)
   

Плоскость β (АВСD) пересекается с прямой ЕF(рис.32б).

1. 
   Через прямую ЕFпровести плоскость (αП₂); α₂ ≡Е₂F ₂;
   
2. 
   Построить линию пересечения плоскостей β и α: (1 - 2) =( β ∩ α);
   
3. 
   Отметить точку К пересечения линии EFи(1 - 2): К = (ЕF) ∩ (1 - 2); К₁ = (Е₁F₁) ∩ (1₁ - 2₁).
   

Решение задачи завершается определением видимых участков прямой относительно плоскости β, считая ее непрозрачной.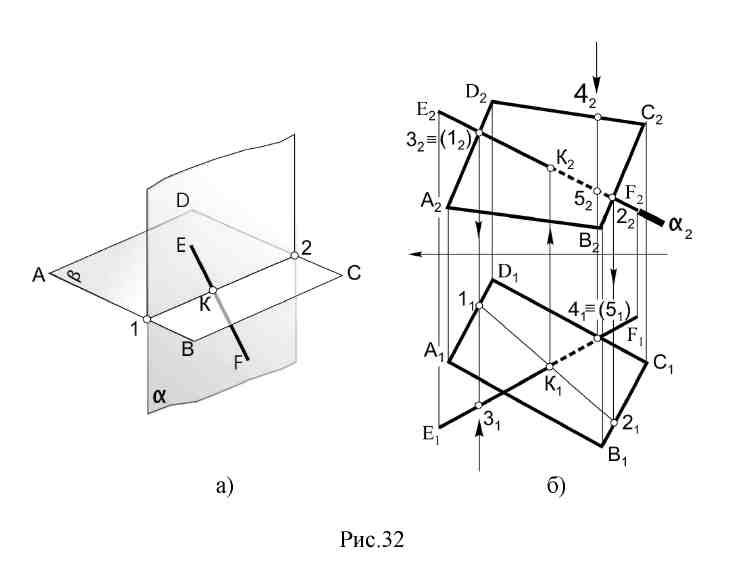



4.7. Вопросы для самопроверки.

1. 
   В каком случае прямая параллельна плоскости?
   
2. 
   Назовите признак параллельности плоскостей.
   
3. 
   Назовите признак перпендикулярности прямой плоскости.
   
4. 
   Сформулируйте условие перпендикулярности двух плоскостей.
   
5. 
   Как построить линию пересечения плоскостей?
   
6. 
   Какова последовательность построения точки пересечения прямой с плоскостью общего положения.
   

5. Лекция 5. Способы преобразования проекций.

5.1. Общие положения.

Способы преобразования проекций предназначены для решения метрических задач, связанных с определением действительных размеров и формы изображаемых на эпюре геометрических объектов.

Преобразование проекций имеет целью привести данные геометрические образы в некоторое частное положение относительно плоскостей проекций. Новое положение выбирается так, чтобы упростилось решение поставленной задачи.

Изменять положение заданных образов по отношению к плоскостям проекций можно двумя путями:

1. 
   геометрический объект в пространстве остается неподвижным, изменяет положение аппарат проецирования (способ замены плоскостей проекций);
   
2. 
   геометрический объект изменяет свое положение в пространстве, аппарат проецирования неподвижен (способы вращения, способ перемещения).
   

5.2. Способ замены плоскостей проекций.

Сущность способа заключается в том, что при неизменном положении объекта в пространстве производится замена данной системы плоскостей новой системой взаимно - перпендикулярных плоскостей. При переходе к новой системе одну из плоскостей проекций заменяют новой плоскостью так, чтобы заданный геометрический элемент (прямая, плоскость …) занял частное положение и проецировался без искажения на новую плоскость проекций.

При этом должны соблюдаться два условия:

1. 
   вновь вводимая плоскость должна быть перпендикулярна оставшейся плоскости;
   
2. 
   направление проецирования к новой плоскости должно быть ортогональ­ным.
   

В системе П₁и П₂задана точка А. (рис. 33).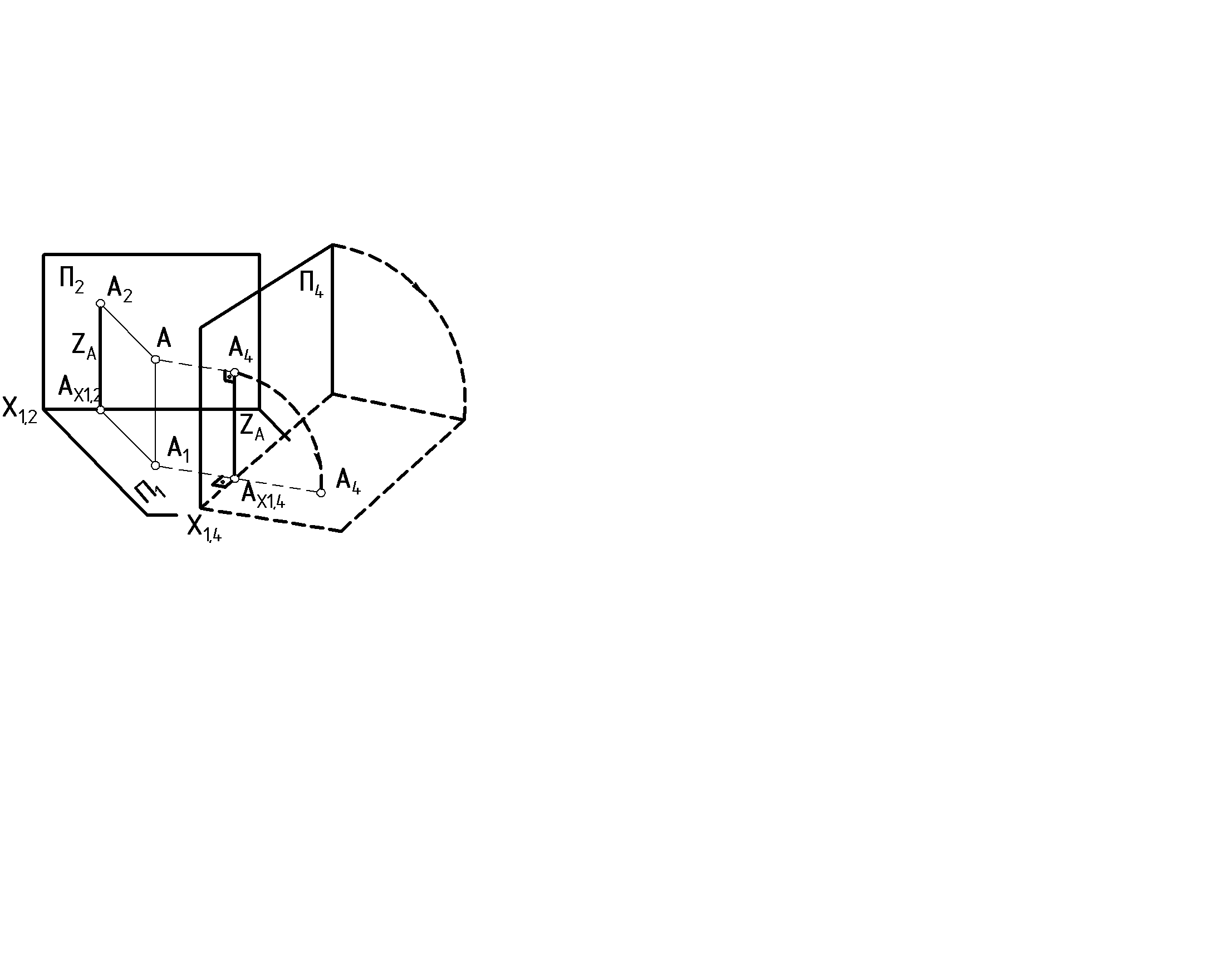


Рис. 33

Плоскость П₂заменяем на плоскость П₄.

П₄П₁, П₄ ∩ П₁ = X_1,4.

Точку А ортогонально спроецируем на плоскость П₄.

Плоскость П₁является общей для старой и новой систем, и поэтому координата Z точки сохраняется.

A₄A_X1,4 = A₂A_X1,2=Z_A

Для получения эпюра плоскость П₄вращением вокруг оси Х_1,4совмещается с плоскостью П₁.

Порядок построения новой проекции точки (рис. 34).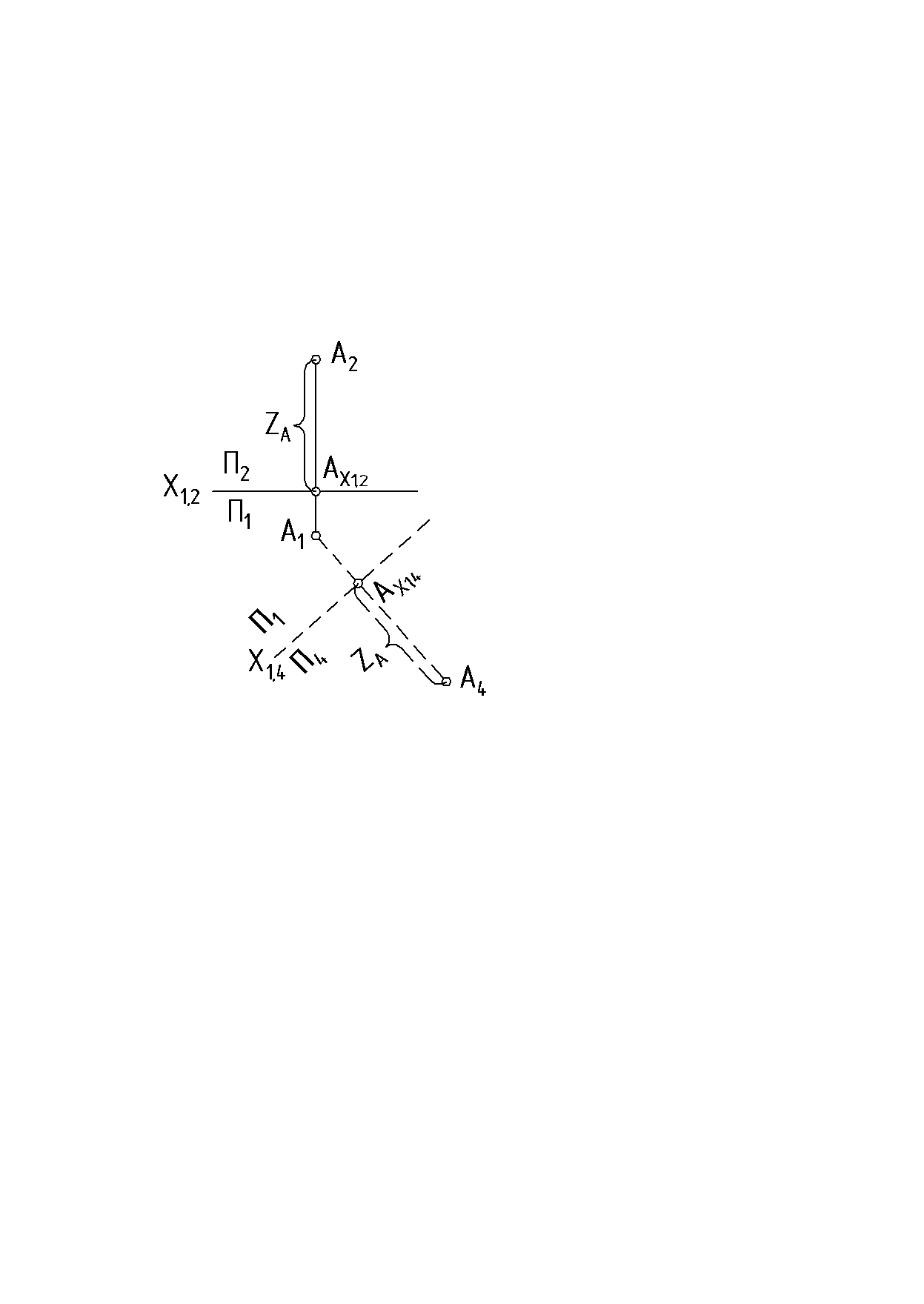




Рис. 34

1. 
   Проводим новую ось проекции Х_1,4
   
2. 
   Проводим линию связи между оставшейся проекцией точки и новой (А₁А₄)  Х_1,4.
   
3. 
   Измеряем координату Z_A точки на замененной плоскости П₂и откладываем ее на новой линии связи от новой оси Х_1,4до новой проекции А_4.
   

5.3. Решение четырех основных задач методом замены плоскостей проекций.

1. Преобразовать чертеж так, чтобы прямая общего положения оказалась прямой уровня (рис. 35).

Новую плоскость проекций П₄, а значит, ось Х_1,4располагаем параллельно одной из проекций прямой.

Х_1,4 || А₁В₁

Далее, исходя из правила построения новой проекции точки, строим проекции А₄и В₄.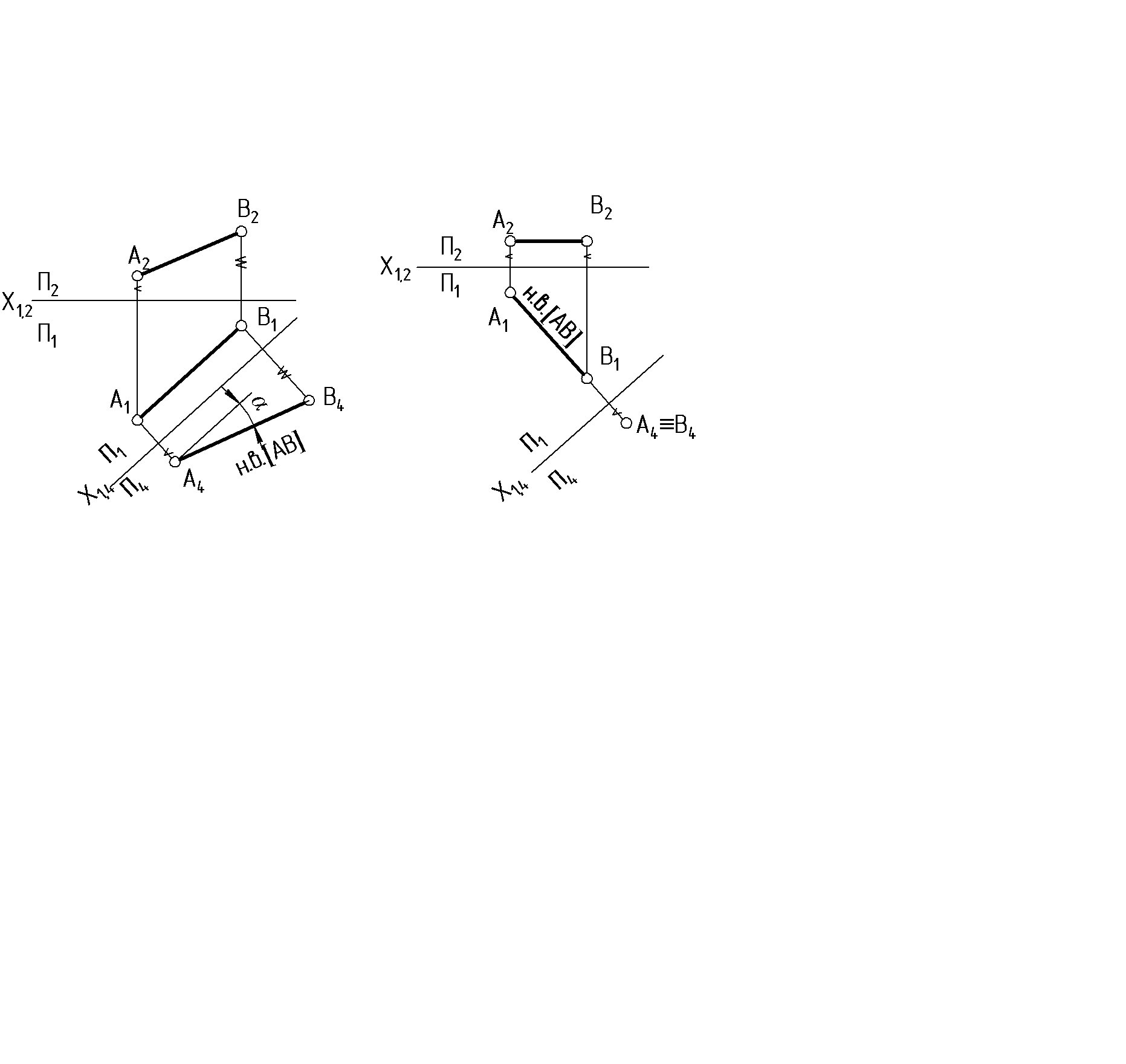



Рис. 35 Рис. 36

2. Преобразовать чертеж так, чтобы прямая уровня оказалась проецирующей, т.е. перпендикулярной новой плоскости проекции (рис. 36).

Исходя из графического признака проецирующей прямой, одна из проекций должна быть перпендикулярна оси проекций А₁В₁Х_1,4.

Далее по правилу строим новые проекции точек А₄и В₄: АВП₄.

3. Преобразовать чертеж так, чтобы плоскость общего положения в новой системе плоскостей проекций стала проецирующей (рис. 37).

Для того чтобы плоскость общего положения (АВС) стала перпендикулярной новой плоскости проекций, необходимо в этой плоскости АВС иметь линию, которая по отношению к новой плоскости проекций была бы перпендикулярна.

Это условие выполнимо с помощью вспомогательной прямой - линии уровня (горизонтали или фронтали) данной плоскости (АВС).

На чертеже проводим ось Х_1,4перпендикулярно горизонтали h : х_1,4h₁; АВСП₄; β - угол наклона плоскости АВС к плоскости П₁.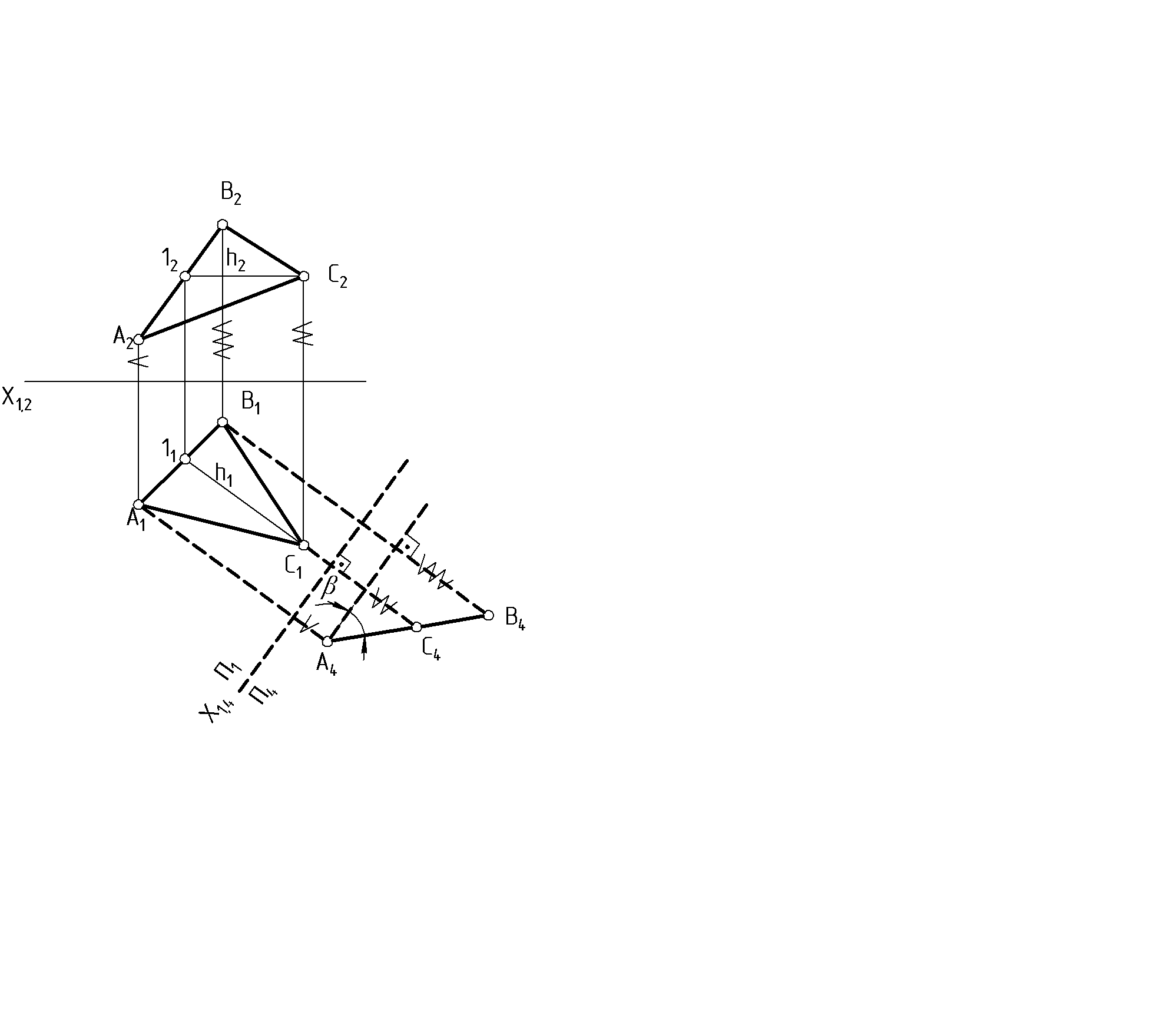



Рис. 37

4. Преобразовать чертеж так, чтобы проецирующая плоскость в новой системе плоскостей стала плоскостью уровня (рис. 38).

Исходя из графического признака плоскости уровня, ось Х_1,4располагаем параллельно плоскости треугольника Х_1,4 || А₁В₁С₁;

АВС || П₄.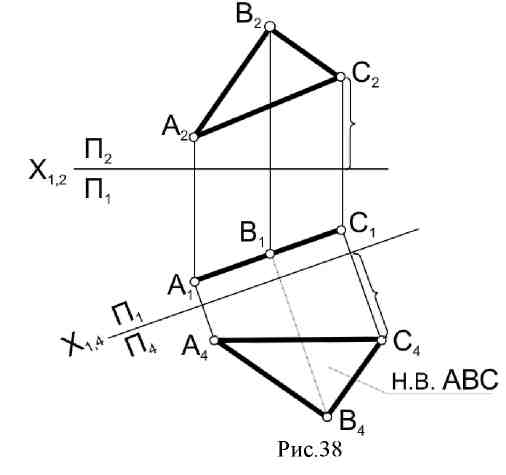

4. 
   
   
   Типы задач, решаемые способом преобразования плоскостей проекций.
   

Путем преобразования проекций возможно решение следующих задач:

1. 
   Определение натуральной величины отрезка прямой и углов его наклона к плоскостям проекций.
   
2. 
   Определение расстояния от точки до прямой.
   
3. 
   Определение расстояния между параллельными прямыми.
   
4. 
   Определение расстояния между скрещивающимися прямыми.
   
5. 
   Определение величины двугранного угла.
   
6. 
   Определение расстояния от точки до плоскости.
   
7. 
   Определение расстояния между параллельными плоскостями.
   
8. 
   Определение истинной величины плоской фигуры.
   
9. 
   Определение угла наклона прямой и плоскости.
   

10. Определение углов наклона плоскости к плоскостям проекций и т.п.

Пример:

Определить расстояние от точки D до плоскости АВС (рис. 39). Для определения искомого расстояния плоскость АВС преобразуем в проецирующую, для этого в ней проведем горизонталь (h) и новую плоскость П₄поставим перпендикулярно h, а значит, Х_1,4перпендикулярно проекции горизонтали (h₁), таким образом, плоскость АВС станет перпендикулярной плоскости П₄Искомое расстояние - ( D₄K₄) - величина перпендикуляра, опущенного из . D₄на линию А₄В₄С₄(проекцию плоскости АВС на плоскость П₄).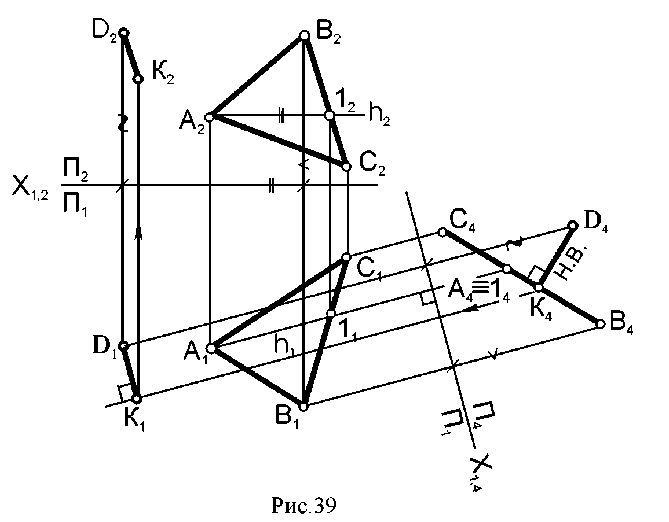